Ejercicio: 3Eva_IT2017_T4 EDP elíptica, placa desplazada
La ecuación del problema en forma contínua:
\frac{\delta ^2 U}{\delta x^2} + \frac{\delta ^2 U}{\delta y^2} = \frac{x}{y} + \frac{y}{x}1 < x < 2
1 < y < 2
Se convierte a la versión discreta usando diferencias divididas centradas

\frac{u[i-1,j]-2u[i,j]+u[i+1,j]}{\Delta x^2} + + \frac{u[i,j-1]-2u[i,j]+u[i,j+1]}{\Delta y^2} = \frac{x_i}{y_j} + \frac{y_j}{x_i}
Se agrupan los términos Δx, Δy semejante a formar un λ al multiplicar todo por Δy2
\frac{\Delta y^2}{\Delta x^2}\Big(u[i-1,j]-2u[i,j]+u[i+1,j] \Big) + + \frac{\Delta y^2}{\Delta y^2}\Big(u[i,j-1]-2u[i,j]+u[i,j+1]\Big) = =\Delta y^2\Big( \frac{x_i}{y_j} + \frac{y_j}{x_i}\Big)\lambda= \frac{\Delta y^2}{\Delta x^2} = 1
por ser los tamaños de paso iguales en ambos ejes, se simplifica la ecuación a usar:
u[i-1,j]-2u[i,j]+u[i+1,j] + + u[i,j-1]-2u[i,j]+u[i,j+1] = =\Delta y^2\Big( \frac{x_i}{y_j} + \frac{y_j}{x_i}\Big)
u[i-1,j]-4u[i,j]+u[i+1,j] + + u[i,j-1]+u[i,j+1] =\Delta y^2\Big( \frac{x_i}{y_j} + \frac{y_j}{x_i}\Big)
Por simplicidad se usará el método iterativo en el ejercicio, por lo que se despeja la ecuación del centro del rombo formado por los puntos,
4u[i,j] = u[i-1,j]+u[i+1,j] + + u[i,j-1]+u[i,j+1] -\Delta y^2\Big( \frac{x_i}{y_j} + \frac{y_j}{x_i}\Big)
u[i,j] = \frac{1}{4}\Big( u[i-1,j]+u[i+1,j] + + u[i,j-1]+u[i,j+1] -\Delta y^2\Big( \frac{x_i}{y_j} + \frac{y_j}{x_i}\Big)\Big)
Iteraciones:
Se utiliza una matriz de ceros para la iteración inicial. En el ejercicio se muestran cálculos para 3 nodos, el resto se realiza con el algoritmo en Python.
Para varias iteraciones se usa Δx =Δy = 1/4 = 0.25
y las ecuaciones para los valores en las fronteras o bordes de la placa
U(x,1)= x \ln (x), U(x,2) = x \ln (4x^{2}),1 \lt x \lt 2 U(1,y)= y \ln(y), U(2,y) = 2y \ln (2y), 1 \lt x \lt 2i=1, j=1
u[1,1] = \frac{1}{4}\Big( u[0,1]+u[2,1] + + u[1,0]+u[1,2] -(0.25)^2\Big( \frac{1.25}{1.25} + \frac{1.25}{1.25}\Big)\Big)
u[1,1] = \frac{1}{4}\Big(1.25 \ln (1.25)+0 + + 1.25 \ln(1.25) + 0 -(0.25)^2\Big( \frac{1.25}{1.25} + \frac{1.25}{1.25}\Big)\Big)
i = 2, j =1
u[2,1] = \frac{1}{4}\Big( u[1,1]+u[3,1] + + u[2,0]+u[2,2] -(0.25)^2\Big( \frac{1.5}{1.5} + \frac{1.5}{1.5}\Big)\Big)
Método iterativo
usando el método iterativo se obtiene los siguientes resultados:
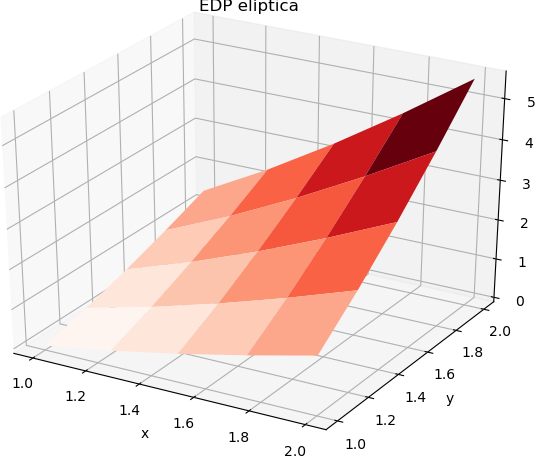
iteraciones: 15 error entre iteraciones: 6.772297286980838e-05 solución para u: [[0. 0.27892944 0.60819766 0.97932763 1.38629436] [0.27892944 0.69781162 1.1792239 1.7127402 2.29072683] [0.60819766 1.1792239 1.8252746 2.53384036 3.29583687] [0.97932763 1.7127402 2.53384036 3.42800537 4.38467039] [1.38629436 2.29072683 3.29583687 4.38467039 5.54517744]] >>>
Algoritmo en Python
# 3Eva_IT2017_T4 EDP elíptica, placa desplazada # método iterativo import numpy as np # INGRESO # longitud en x a = 1 b = 2 # longitud en y c = 1 d = 2 # tamaño de paso dx = 0.25 dy = 0.25 # funciones en los bordes de la placa abajo = lambda x,y: x*np.log(x) arriba = lambda x,y: x*np.log(4*(x**2)) izquierda = lambda x,y: y*np.log(y) derecha = lambda x,y: 2*y*np.log(2*y) # función de la ecuación fxy = lambda x,y: x/y + y/x # control de iteraciones maxitera = 100 tolera = 0.0001 # PROCEDIMIENTO # tamaño de la matriz n = int((b-a)/dx)+1 m = int((d-c)/dy)+1 # vectores con valore de ejes xi = np.linspace(a,b,n) yj = np.linspace(c,d,m) # matriz de puntos muestra u = np.zeros(shape=(n,m),dtype=float) # valores en los bordes u[:,0] = abajo(xi,yj[0]) u[:,m-1] = arriba(xi,yj[m-1]) u[0,:] = izquierda(xi[0],yj) u[n-1,:] = derecha(xi[n-1],yj) # valores interiores # para menos iteraciones mitadx = int(n/2) mitady = int(m/2) promedio = (u[mitadx,0]+u[mitadx,m-1]+u[0,mitady]+u[n-1,mitady])/4 u[1:n-1,1:m-1] = promedio # método iterativo itera = 0 converge = 0 while not(itera>=maxitera or converge==1): itera = itera +1 # copia u para calcular errores entre iteraciones nueva = np.copy(u) for i in range(1,n-1): for j in range(1,m-1): # usar fórmula desarrollada para algoritmo u[i,j] = (u[i-1,j]+u[i+1,j]+u[i,j-1]+u[i,j+1]-(dy**2)*fxy(xi[i],yj[j]))/4 diferencia = nueva-u erroru = np.linalg.norm(np.abs(diferencia)) if (erroru<tolera): converge=1 # SALIDA print('iteraciones: ',itera) print('error entre iteraciones: ',erroru) print('solución para u: ') print(u) # Gráfica import matplotlib.pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D # matrices de ejes para la gráfica 3D X, Y = np.meshgrid(xi, yj) U = np.transpose(u) # ajuste de índices fila es x figura = plt.figure() grafica = Axes3D(figura) grafica.plot_surface(X, Y, U, rstride=1, cstride=1, cmap=cm.Reds) plt.title('EDP elíptica') plt.xlabel('x') plt.ylabel('y') plt.show()