Ejercicio: 3Eva_IT2018_T2 Drenaje de estanque
literal a
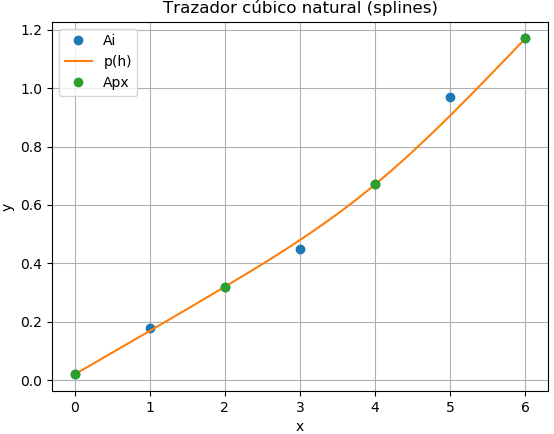
Se usa interpolación para encontrar los polinomios que pasan por los puntos seleccionados.
El error de A(5) se obtiene como la diferencia entre el valor de la tabla y el polinomio del tramo [4,6] evaluado en el punto.
ordenado: [6 5 4 3 2 1 0] hi: [0 1 2 3 4 5 6] Ai: [ 0.02 0.18 0.32 0.45 0.67 0.97 1.17] puntos seleccionados: h1: [0, 2, 4, 6] A1: [ 0.02 0.32 0.67 1.17] Polinomios por tramos: x = [0,2] 0.000416666666666669*x**3 + 0.148333333333333*x + 0.02 x = [2,4] 0.00416666666666666*x**3 - 0.0224999999999999*x**2 + 0.193333333333333*x - 0.00999999999999984 x = [4,6] -0.00458333333333333*x**3 + 0.0824999999999999*x**2 - 0.226666666666666*x + 0.549999999999999 error en px(5): 0.0637499999999998
se observa que la evaluación se realiza para el polinomio entre [4,6]
Desarrollo en Python
# 3ra Evaluación I Término 2018 # Tema 2. Drenaje de Estanque import numpy as np import matplotlib.pyplot as plt import sympy as sym def traza3natural(xi,yi): # Trazador cúbico natural, splines # resultado: polinomio en forma simbólica n = len(xi) # Valores h h = np.zeros(n-1, dtype = float) for j in range(0,n-1,1): h[j] = xi[j+1] - xi[j] # Sistema de ecuaciones A = np.zeros(shape=(n-2,n-2), dtype = float) B = np.zeros(n-2, dtype = float) S = np.zeros(n, dtype = float) A[0,0] = 2*(h[0]+h[1]) A[0,1] = h[1] B[0] = 6*((yi[2]-yi[1])/h[1] - (yi[1]-yi[0])/h[0]) for i in range(1,n-3,1): A[i,i-1] = h[i] A[i,i] = 2*(h[i]+h[i+1]) A[i,i+1] = h[i+1] B[i] = 6*((yi[i+2]-yi[i+1])/h[i+1] - (yi[i+1]-yi[i])/h[i]) A[n-3,n-4] = h[n-3] A[n-3,n-3] = 2*(h[n-3]+h[n-2]) B[n-3] = 6*((yi[n-1]-yi[n-2])/h[n-2] - (yi[n-2]-yi[n-3])/h[n-3]) # Resolver sistema de ecuaciones r = np.linalg.solve(A,B) # S for j in range(1,n-1,1): S[j] = r[j-1] S[0] = 0 S[n-1] = 0 # Coeficientes a = np.zeros(n-1, dtype = float) b = np.zeros(n-1, dtype = float) c = np.zeros(n-1, dtype = float) d = np.zeros(n-1, dtype = float) for j in range(0,n-1,1): a[j] = (S[j+1]-S[j])/(6*h[j]) b[j] = S[j]/2 c[j] = (yi[j+1]-yi[j])/h[j] - (2*h[j]*S[j]+h[j]*S[j+1])/6 d[j] = yi[j] # Polinomio trazador x = sym.Symbol('x') polinomio = [] for j in range(0,n-1,1): ptramo = a[j]*(x-xi[j])**3 + b[j]*(x-xi[j])**2 + c[j]*(x-xi[j])+ d[j] ptramo = ptramo.expand() polinomio.append(ptramo) return(polinomio) # PROGRAMA ------------------------- hi = np.array([6, 5, 4, 3, 2, 1, 0]) Ai = np.array([1.17, 0.97, 0.67, 0.45, 0.32, 0.18, 0.02]) xk = 5 # PROCEDIMIENTO LITERAL a # reordena en forma ascendente ordenado = np.argsort(hi) hi = hi[ordenado] Ai = Ai[ordenado] # Selecciona puntos xi = [0,2,4,6] fi = Ai[xi] n = len(xi) polinomio = traza3natural(xi,fi) # literal a, estima error px = polinomio[2] pxk = px.subs('x',xk) errado = np.abs(Ai[xk] - pxk) # SALIDA print('ordenado: ', ordenado) print('hi: ', hi) print('Ai: ', Ai) print('puntos seleccionados:') print('h1: ', xi) print('A1: ', fi) print('Polinomios por tramos: ') for tramo in range(1,n,1): print(' x = ['+str(xi[tramo-1])+','+str(xi[tramo])+']') print(str(polinomio[tramo-1])) print('error en px(5): ', errado) # GRAFICA # Puntos para grafica en cada tramo resolucion = 10 # entre cada par de puntos xtrazado = np.array([]) ytrazado = np.array([]) tramo = 1 while not(tramo>=n): a = xi[tramo-1] b = xi[tramo] xtramo = np.linspace(a,b,resolucion) ptramo = polinomio[tramo-1] pxtramo = sym.lambdify('x',ptramo) ytramo = pxtramo(xtramo) xtrazado = np.concatenate((xtrazado,xtramo)) ytrazado = np.concatenate((ytrazado,ytramo)) tramo = tramo + 1 # GRAFICA # puntos originales plt.plot(hi,Ai,'o',label = 'Ai') # Trazador cúbico plt.plot(xtrazado,ytrazado, label = 'p(h)') plt.plot(xi,fi,'o', label = 'Apx') plt.title('Trazador cúbico natural (splines)') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid() plt.show()
Literal b
TAREA