s3Eva_IT2019_T1 Ecuaciones simultáneas

Ejercicio: 3Eva_IT2019_T1 Ecuaciones simultáneas

Para plantear la intersección de las ecuaciones se pueden simplificar como:

y_1 = -x^2 +x + 0.75 y+5xy=x^3 y(1+5x)=x^3 y_2=\frac{x^3}{1+5x}

Quedando dos ecuaciones simplificadas:

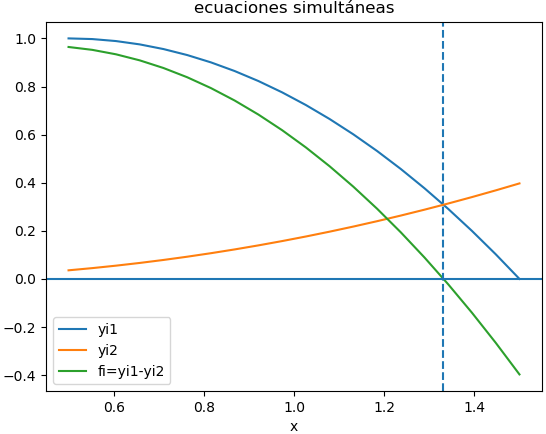
y_1 = -x^2 +x + 0.75 y_2 = \frac{x^3}{1+5x}

cuyas gráficas son:

dónde se puede observar la intersección alrededor de 1.3

Restando ambas ecuaciones, se tiene que encontrar el valor de x para que el resultado sea cero.

y_1(x)-y_2(x)= -x^2 +x + 0.75 -\frac{x^3}{1+5x} f(x) = -x^2 +x + 0.75 -\frac{x^3}{1+5x} = 0

Para encontrarla derivada se procesa la expresión:

(1+5x)(-x^2 +x + 0.75) -x^3 = 0(1+5x) -6x^3+4x^2+4.75x+0.75 = 0 f'(x)= -18x^2 +8x + 4.75

Se usa el punto inicial x₀=1 definido en el enunciado y se realizan las iteraciones siguiendo el algoritmo.

Se tiene que la raiz es:

raiz en:  1.3310736382369661
 [  xi, 	 xnuevo,	 fxi,	 dfxi, 	 tramo]
[[ 1.000e+00  1.111e+00  5.833e-01 -5.250e+00  1.111e-01]
 [ 1.111e+00  1.160e+00  4.173e-01 -8.583e+00  4.862e-02]
 [ 1.160e+00  1.193e+00  3.353e-01 -1.018e+01  3.293e-02]
 [ 1.193e+00  1.217e+00  2.766e-01 -1.131e+01  2.445e-02]
 [ 1.217e+00  1.236e+00  2.313e-01 -1.218e+01  1.899e-02]
 [ 1.236e+00  1.251e+00  1.951e-01 -1.286e+01  1.517e-02]
....
]

---

Algoritmo en Python

# 3Eva I T 2019 ecuaciones simultaneas
import numpy as np
import matplotlib.pyplot as plt

def newton_raphson(funcionx, fxderiva, xi, tolera):
    '''
    funciónx y fxderiva son de forma numérica
    xi es el punto inicial de búsqueda
    '''
    tabla = []
    tramo = abs(2*tolera)
    while (tramo>=tolera):
        fxi = funcionx(xi)
        dfxi = fxderiva(xi)
        xnuevo = xi - fxi/dfxi
        tramo = abs(xnuevo-xi)
        tabla.append([xi,xnuevo,fxi,dfxi,tramo])
        xi = xnuevo
    return(xi,tabla)

# INGRESO
y1 = lambda x: -x**2 +x +0.75
y2 = lambda x: (x**3)/(1+5*x)
a = 0.5
b = 1.5
muestras = 20

f = lambda x: -x**2+x+0.75-x**3/(1+5*x)
df = lambda x: -18*(x**2)+8*x +4.75
tolera = 1e-4
x0 = 1

# PROCEDIMIENTO
# datos para la gráfica
xi = np.linspace(a,b,muestras)
yi1 = y1(xi)
yi2 = y2(xi)
fi = f(xi)
# determina raiz
raiz, tabla = newton_raphson(f, df, x0, tolera)
tabla = np.array(tabla)

# SALIDA
np.set_printoptions(precision=3)
print('raiz en: ',raiz)
print(' [  xi, \t xnuevo,\t fxi,\t dfxi, \t tramo]')
print(tabla)

# Gráfica
plt.plot(xi,yi1, label ='yi1')
plt.plot(xi,yi2, label ='yi2')
plt.plot(xi,fi, label ='fi=yi1-yi2')
plt.axvline(raiz,linestyle='dashed')
plt.axhline(0)
plt.xlabel('x')
plt.legend()
plt.title('ecuaciones simultáneas')
plt.show()