3ra Evaluación 2022-2023 PAO I. 13/Septiembre/2022
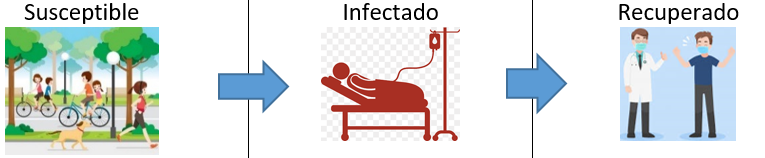
Tema 3. (35 puntos) En genética, el modelo de selección híbrida representa la porción de la población que tiene ciertas características a lo largo del tiempo medido en generaciones (h=1).
 Para una población de escarabajos, la rapidez de transferencia que una característica D pasa de una generación a la siguiente está dada por:
Para una población de escarabajos, la rapidez de transferencia que una característica D pasa de una generación a la siguiente está dada por:
Las constantes a, b y k dependen de las características genéticas estudiadas.
Al inicio del estudio, t=0, se encuentra que la mitad de la población tiene la característica D, y(0)=0.5. El factor k=0.26 considera la trasferencia al combinarse los especímenes “Sin D” y “con D”. Use los valores de a=2 y b=1.
a) Realice el planteamiento del problema de la Ecuación Diferencial Ordinaria usando el método de Runge-Kutta de 4to Orden
b) Desarrolle al menos tres iteraciones usando las expresiones completas.
c) estime la cota de error de la solución.
d) Adjunte el desarrollo completo usando un algoritmo con Python para las próximas 10 generaciones. tabla y gráfica.
Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d (5 puntos), gráfica(5puntos)
Referencias: Larson. Cálculo aplicado, 7ma Ed. Apéndice C, ejemplo 4. https://college.cengage.com/mathematics/larson/calculus_applied/7e/students/appendices/appendix_c04.pdf
Los mecanismos del cambio. https://www.sesbe.org/evosite/evo101/IIIBMechanismsofchange.shtml.html