Etiqueta: interpolación polinómica

1ra Evaluación II Término 2009-2010. 1/Diciembre/2009. ICM00158

Tema 3. Para el control de los accidentes de tránsito, se requiere modelar un factor de riesgo de que ocurra un accidente de tránsito en cierta avenida, en función del número de vehículos que circulan por ella a la semana.

 Por observación directa se han determinado los siguientes factores:

“Número de vehículos que circulan por la avenida a la semana” vs “Factor de riesgo”

vehículos	10000	7000	6000	5000
Factor de riesgo	0.8	0.5	0.4	0.2

Empleando toda la información de la tabla anterior, estime con un polinomio de Lagrange el factor de riesgo que tendrá la avenida si el número de vehículos que circula a la semana es 6500.

---

vehiculos = np.array([10000, 7000, 6000, 5000])
riesgo = np.array([0.8, 0.5, 0.4, 0.2])

1ra Evaluación I Término 2009-2010. 7/Julio/2009. ICM00158

Tema 3. Una empresa que vende cierto producto ha observado que su demanda depende del precio al que se lo vende (P en $/unidad) y también del precio al que la competencia vende un producto de similares características (Q en $/unidad).

Recopilando información histórica respecto a lo que ha sucedido en el pasado, se observó que la demanda diaria (unidades vendidas por día) de este producto fueron de:

Q\P	1	1.1	1.2
1	100	91	83
1.1	110	100	92
1.2	120	109	100
1.3	130	118	108

Use todos los datos dados y el polinomio de interpolación de Lagrange para estimar los Ingresos mensuales de la empresa por la venta de este producto si decide venderlo a $1.15 por unidad y conoce que la competencia estableció un precio de $1.25 por unidad.

1ra Evaluación II Término 2008-2009. 9/Diciembre/2008. ICM02188 Métodos Numéricos

Tema 3. Se dispone de los datos (x, f(x)), en donde x es un valor de inversión y f(x) es un valor de ganancia, ambos en miles de dólares:

 

inversión	ganancia
3.2	5.12
3.8	6.42
4.2	7.25
4.5	6.85

para analizar éste comportamiento se propone usar el siguiente modelo:

f(x) = a_1 x^3 + a_2 x^2 + a_3 x + a_4

a) Sustituya cada dato (x, f(x)) en el modelo y obtenga un sistema de ecuaciones lineales.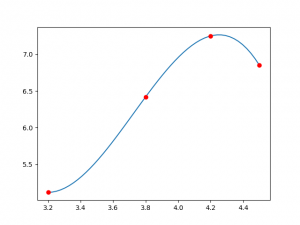

b) Obtenga los coeficientes a_i resolviendo el sistema lineal con un método numérico directo.

c) Con el modelo f(x), use el método de la Bisección para calcular cuánto debe invertirse si se desea que la ganancia sea de 6.0 (miles de dólares).
Precisión: dos decimales exactos.

---

[[3.2, 5.12],
 [3.8, 6.42],
 [4.2, 7.25],
 [4.5, 6.85]]

1ra Evaluación II Término 2008-2009. 9/Diciembre/2008. ICM00158

Tema 2. El índice enfriador del viento I es una función que depende de dos factores: La temperatura real T y la velocidad del viento v; es decir I=f(T,v).

La siguiente tabla registra los valores de I recogidos en cierto momento por un investigador en los páramos del Cotopaxi. Por ejemplo, cuando la temperatura real es de 5 grados Celcius y el viento de 20 Km/hora, el índice I = f(5, 20) =1 , que quiere decir que la temperatura que se siente en estas condiciones es de 1 grado, aunque no sea la temperatura real.

T\v	5	10	15	20
5	4	2	2	1
0	-2	-3	-4	-5
-5	-8	-10	-11	-12

Usando interpolación polinomial, estimar la temperatura que sentirá una persona situada en un lugar en el que la temperatura real es de 2 grados y la velocidad del viento es 25 Km/hora.

1ra Evaluación I Término 2008-2009. 8/Julio/2008. ICM00158

Tema 3. Dada la tabla:

t	v(t)
3	65.041
5	64.385
7	y
9	63.210
x	62.576
13	61.993
15	61.417

Aproximar los valores de x,y con ayuda de polinomios de Lagrange

1ra Evaluación III Término 2007-2008. 3/Marzo/2008. ICM00158

Tema 2. La función de producción llamada Cobb-Douglas relaciona funcionalmente a los insumos de capital y trabajo necesarios para producir de la manera más óptima de una determinada cantidad de un bien.

Y = f(K,L) es la cantidad máxima del bien que se puede producir dados los insumos utilizados de capital y trabajo. K y L representan las cantidades de capital y trabajo respectivamente.

En la industria de lácteos se han observado los siguientes valores óptimos de producción Y (en miles de Kg) para diferentes valores de L (número de trabajadores)  y capital invertido K (en miles de dólares).

L\K	10	20	30	40
0	0	0	0	0
10	11.0000	13.0813	14.4768	15.5563
20	18.4997	22.0000	24.3470	26.1626
30	25.0746	29.8189	33.0000	35.4608

a. Determinar usando el polinomio de interpolación de Lagrange, ¿cuál será la producción óptima de lácteos en una empresa que emplea 25 trabajadores y que invierte un capital de $ 25000 en el plan de producción?

b.  Una empresa que tiene 25 trabajadores desea producir 30000 Kg de lácteos. ¿cuánto dinero deberá invertir?, use el polinomio de interpolación y el método de Newton con una precisión de 10^-5

---

Referencia: Wikipedia/Cobb-Douglas

M = np.array([[0, 0, 0, 0],
              [11.0000, 13.0813, 14.4768, 15.5563],
              [18.4997, 22.0000, 24.3470, 26.1626],
              [25.0746, 29.8189, 33.0000, 35.4608]])
li = np.array([0.0, 10, 20, 30])
kj = np.array([10.0, 20, 30, 40])

1ra Evaluación II Término 2007-2008. 4/Diciembre/2007.
ICM00158

Tema 3. Dado los datos de una función:

f(0.50) = 1.648
f(0.65) = 1.915
f( x  ) = 2.117
f(0.80) = 2.225
f(0.95) = 2.5857

Determinar el valor de x, usando interpolación inversa.

---

xi = np.array([0.50 , 0.65 , x, 0.80 , 0.95  ])
fi = np.array([1.648, 1.915, 2.117, 2.225, 2.5857])

Use otra forma para repasar otros conceptos:
– Encuentre el polinomio de interpolación entre los puntos disponibles,
– Use un método de búsqueda de raiz para encontrar el punto x.