Etiqueta: método de Newton-Raphson

1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

Tema 4. (20 puntos) La siguiente ecuación permite calcular la concentración de un químico en un reactor, donde se tiene una mezcla completa.

$C = C_{ent} ( 1 - e^{-0.04t})+C_{0} e^{-0.03t}$

Si la concentración inicial es C₀ = 4 y la concentración de entrada es C_ent = 10, use el método de Newton-Raphson con t₀ = 0, para aproximar el tiempo requerido para que el valor de C sea 93% de C_ent.

Encuentre un intervalo en donde la convergencia está garantizada.

Rúbrica: intervalo (5 puntos), iteraciones (10 puntos), convergencia (5 puntos)

3ra Evaluación I Término 2019-2020. 10/Septiembre/2019. MATG1013

Tema 1. (30 Puntos).  Determine las raíces de las ecuaciones simultáneas siguientes:

$y = -x^2 +x + 0.75$ $y+5xy=x^3$

a. Realice un bosquejo para cada ecuación
b. Use el método de Newton-Raphson con x₀=1 , y₀=0.75, realice 3 iteraciones
c. Estime el orden del error

Rúbrica: literal a (5 puntos), literal b planteo (5 puntos), iteraciones (15 puntos), literal c (5 puntos)

3ra Evaluación I Término 2018-2019. 11/Septiembre/2018. MATG1013

Tema 1. (30 puntos) Encuentre las raíces de las ecuaciones simultaneas siguientes:

$(x-4)^2 + (y-4)^2 = 5$ $x^2 + y^2 = 16$

a) Use el enfoque gráfico para obtener los valores iniciales.

b) Encuentre aproximaciones refinadas con el Método de Newton-Raphson

Rúbrica: literal a (10 puntos), literal b  (20 puntos)

---

Referencia: Un asteroide dos veces más grande que un avión Boeing 747 pasará muy cerca la Tierra. https://www.eluniverso.com/noticias/2018/08/28/nota/6927335/asteroide-dos-veces-mas-grande-que-avion-pasara-muy-cerca-tierra

Europa Press 28 de agosto, 2018 – 11h51

3ra Evaluación I Término 2012-2013. 11/Septiembre/2012. ICM00158

Tema 1. Dado el sistema de ecuaciones no lineales

$3x^2 + 3y^2 - 15 = 0$ $2x^2y- 1 = 0$

x∈R;   y ≥ 1

a. Realice un bosquejo gráfico y especifique el número de soluciones del sistema.

b. Determine la ecuación en términos de una variable para resolver el sistema.

c. Justifique un intervalo donde se encuentre la solución de la ecuación planteada en literal b.

d. Aproxime la solución empleando el método de Newton-Raphson con tolerancia de 10^-6.

e. Escriba correctamente la solución hallada.

1ra Evaluación II Término 2017-2018. 28/Noviembre/2017. MATG1013

Tema 2. (25 puntos) Determine una raiz de las ecuaciones no lineales simultaneas siguientes:

y = – x² + x + 0.75
y + 5xy = x²

a) Bosqueje una gráfica y seleccione X⁽⁰⁾

b) Use el método de Newton en dos variables y realice tres iteraciones.

Rúbrica: Bosquejar la gráfica hasta 5%, Plantear el método hasta 5%, Calcular el Jacobiano hasta 5% Hacer tres iteraciones, estimando el error hasta 10%.

1ra Evaluación I Término 2015-2016. 7/julio/2015. ICM00158

Tema 1. (25 puntos)
a) Sea:

f ∈ C∞[a, b] ,
∃p ∈ [a, b] ,
tal que f(p)=0 y 
f'(p) ≠ 0,

demuestre que existe un intervalo que contiene a p, tal que el método de Newton-Raphson converge para cualquier p₀ que pertenece a dicho intervalo.

b) El precio de demanda de un producto está modelado mediante la ecuación:

$y = 10 e^{-x} + 4$

y el precio de la oferta está modelado mediante la ecuación :

$y = 10 x^{2} + 2$

utilizando el método de Newton, plantee la ecuación y encuentre un intervalo de convergencia.

c) Encuentre el precio y demanda donde las curvas se interceptan (equilibrio).

Rúbrica: literal a 7 puntos, literal b (8 puntos), literal c (10 puntos)

 

1ra Evaluación II Término 2014-2015. 9/Diciembre/2013. ICM00158

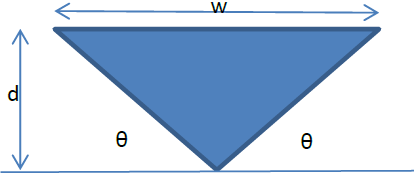
Tema 1. Usted tiene que diseñar un canal triangular abierto para transportar una corriente de deshechos desde una planta química hasta un depósito de estabilización de desechos. 

La velocidad media aumenta con el radio hidráulico,

$R_h = \frac{A}{P}$,

donde A es el área y P es el perímetro mojado de la sección transversal.

El perímetro mojado es la longitud
de los lados y fondo del canal que están bajo el agua

Como la razón del flujo máximo corresponde a la velocidad máxima, el diseño óptimo corresponde a un valor θ que maximice R_h. Considere d=1 unidad.

a) Encuentre un modelo para calcular R_h en función de θ.

b) Obtenga la ecuación para encontrar el máximo.

c) Encuentre un intervalo de existencia y un intervalo de convergencia tal que el método de Newton, y

d) Aproxime θ con una precisión de 0.0001.

Nota: Si no logra encontrar el modelo en el literal a) utilice la siguiente ecuación
$R_h= \frac{d \cos(\theta)}{2(1 + \cos (\theta))}$

---

Referencia: Chapra Problemas 16.11 p442 pdf466.

Siendo c la hipotenusa de un triángulo del canal, la formula queda en función de la profundidad del canal d.

$p = w + 2c$ $\frac{w}{2} = c \cos (\theta)$ $d = c \sin (\theta)$ $c = \frac{d}{sin(\theta)}$ $\frac{w}{2} = \frac{d}{sin(\theta)} \cos(\theta)$ $w = 2d\frac{ \cos(\theta)}{sin(\theta)}$

perimetro p  es entonces:

$p = 2d\frac{ \cos(\theta)}{sin(\theta)} + 2\frac{d}{sin(\theta)}$ $p = 2d\frac{ \cos(\theta)+1}{sin(\theta)}$

continue calculando el área y encuentre la fórmula para el problema …

1ra Evaluación I Término 2012-2013. 3/Julio/2012. ICM00158

Tema 1. (30 puntos). Determine de ser posible, los puntos de la curva

$y=ln(x)$

para x>0, más cercanos al origen de coordenadas.

a) Plantee la ecuación que permita resolver matemáticamente el problema.

b) Determine de ser posible un intervalo de la solución a la ecuación planteada en el literal anterior.

c) Aproxime la solución numérica de la ecuación planteada, empleando el método de Newton-Raphson con tolerancia de 10⁻⁶. Mostrar la tabla de resultados respectiva.

d) Escriba las coordenadas del punto encontrado: (x,y)

1ra Evaluación II Término 2011-2012. 29/Noviembre/2011. ICM02188 Métodos Numéricos

Tema 1. Para que f(x) sea una función de probabilidad, se tiene que cumplir que su integral en el dominio de x debe tener un valor igual a 1.

Encuentre el valor de b para que la función

$f(x) = 2 x^2+x$

sea una función de probabilidad en el dominio [0,b].

Use la fórmula de Newton en la ecuación no lineal resultante. error tolerado=0.0001