Etiqueta: raíces de ecuaciones

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

Tema 1 (30 puntos) La trayectoria automática de un drone espía en un territorio de guerra esta descrita por x₁(t), y₁(t).
Drone
x₁(t) = cos(t)
y₁(t) = sin(2 t)

Antidrone
x₂(t) = sin(0.75 t)
y₂(t) = k t

Durante un intervalo de tiempo t entre [0,10] segundos, se dispara un misil antidrone con trayectoria descrita por x₂(t), y₂(t). El antidrone tiene un parámetro de control constante denominado k para y₂(t) que se establece antes del disparo.

Encuentre el valor de k que produce el impacto que destruye el Drone.

Para que se produzca el impacto, deben coincidir las coordenadas x,y para ambas trayectorias, al mismo valor de tiempo.

a) Realice el planteamiento del problema usando inicialmente las trayectorias en el eje x, donde para el intervalo de operación del misil antidrone, se observa más de un impacto.

b) Usando el método de Newton-Raphson encuentre el valor de t en el cual se pretende realizar el impacto al drone. Realice al menos 3 iteraciones de forma analítica, use tolerancia de 10^-4,

c) Realice el análisis de la convergencia del método.

d) Con el resultado de t anterior, determine el valor de la constante k para la expresión de y₂(t) que asegura el impacto contra el drone.

Rúbrica: literal a (5 puntos), iteraciones (9 puntos), errores entre iteraciones(6 puntos), análisis de convergencia(5 puntos), literal d(5 puntos)

Referencia: Domo de Hierro, así funciona el escudo antimisiles de Israel. CNN en español. 15-mayo-2021. https://www.youtube.com/watch?v=idikebBCXA0

Lo que hay que saber sobre los misiles hipersónicos disparados por Rusia contra Ucrania. cnnespanol.cnn.com 10-mayo-2022. https://cnnespanol.cnn.com/2022/05/10/misiles-hipersonicos-rusia-ucrania-trax/

1ra Evaluación 2021-2022 PAO II. 24/Noviembre/2021

Tema 2. (30 puntos) En un enlace radioeléctrico, se denomina “Zona de Fresnel” al espacio entre un emisor y receptor debe estar libre para minimizar atenuaciones a la onda de propagación.

Una obstrucción es una parte del perfil del terreno que se encuentra dentro de la Zona de Fresnel. El perfil del terreno es la expresión del polinomio del tema anterior P₃(d₁) en el intervalo [0,1300].

Cuando las antenas del transmisor y receptor se encuentran a la misma altura, la parte inferior del lóbulo, f(d₁), se determina a partir de las siguientes fórmulas:

Considere los valores de las constantes h_antena= 100 m, n =1, λ=0.3278, d_enlace=3700 m

Para analizar la obstrucción, se debe determinar los puntos de intersección entre P₃(d₁) y f(d₁)

a. Establezca un intervalo de análisis para cada raíz.

b. Realice al menos 3 iteraciones con el método de la Bisección para encontrar la primera raíz (izquierda)

c. Desarrolle al menos 3 iteraciones con el método del Punto fijo para encontrar el segundo punto (derecha)

d. Realice al menos 3 iteraciones con el método de Newton-Raphson para determinar la altura del perfil que genera el mayor obstáculo dentro del intervalo (altura máxima).

Rúbrica: literal a (4 puntos), literal b (10 puntos), literal c (10 puntos), literal d (6 puntos)

Referencia: Zona de Fresnel, https://youtu.be/v371pPLdf_c

3ra Evaluación 2021-2022 PAO I. 14/Septiembre/2021

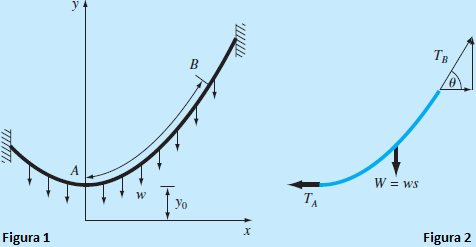
Tema 2 (20 puntos) Continuando con el ejercicio del tema anterior de la carga con dos cables, se requiere encontrar:

a) El valor de θ para el cual la tensión en los dos cables es la mínima posible. Use un algoritmo para encontrar las raíces, es decir T_CA=T_CB

b) Desarrolle al menos 2 iteraciones

c) El valor correspondiente de la tensión.

Nota: Plantear la solución del problema anterior como una función en Python, para usarla como parte del desarrollo de éste tema

Rúbrica: Planteamiento completo del ejercicio (5 puntos), desarrollo de expresiones  (10 puntos), literal b (5 puntos)

1ra Evaluación 2021-2022 PAO I. 6/Julio/2021

Tema 1. (30 puntos) La sucesión mostrada puede ser calculada de forma recursiva para un valor inicial x₀.

$x_n = ln \Bigg(\frac{1}{2+x_{n-1}} \Bigg)$

n = 1, 2, 3, …
x₀ = -0.45

a. Realice 7 iteraciones con la sucesión, tabule y grafique los resultados.

Considerando solamente el intervalo  [-0.5,-0.4]

b. ¿Se puede afirmar que para todo valor inicial x₀ la sucesión converge? Justifique su respuesta.

En algoritmos de computadora, la forma recursiva de la sucesión puede consumir rápidamente recursos, por lo que se plantea encontrar el valor al que converge la sucesión usando siguiente ecuación:

$x +ln(x+2) = 0$

x₀ = -0.45

c. Encuentre el valor que resuelve la ecuación usando el método de Newton-Raphson con tolerancia de 10^-4. Realice al menos 3 iteraciones completas y comente sobre la convergencia.

d. Presente sus conclusiones y recomendaciones para los resultados obtenidos entre el literal b y c.

Rúbrica: literal a (5 puntos), literal b (3 puntos), literal c, verifica intervalo (4 puntos), iteraciones (10 puntos), convergencia (5 puntos), literal d (4 puntos)

 

3ra Evaluación 2020-2021 PAO I. 22/Septiembre/2020

Tema 1. (30 puntos) Calcule el punto de la curva en el plano x-y definida por la función

$y = e^{-x} , x ∈ R$

que se encuentra más cercano al punto(1, 1).

a. Encuentre un intervalo apropiado para aproximar este valor mediante el método de Newton.

b. Usando este método, elabore una tabla que contenga las columnas de la tabla mostrada:

i	xi	f(xi)	Ei
0
1
2
3

donde f(x) = 0 define el problema a resolver y

E_i = |x_i+1 − x_i|, i≥0.

Use como criterio de parada E_i ≤ 10⁻⁷.
Para los cálculos utilice todos los decimales que muestra la calculadora.

Rúbrica: literal a (5 puntos), planteamiento del método (5 puntos). iteraciones (15 puntos), cálculo de errores (5 puntos)

Referencia: NASA: Cinco asteroides se aproximan a la Tierra; los dos primeros este fin de semana. 11 de Julio, 2020. https://www.eluniverso.com/noticias/2020/07/11/nota/7901811/nasa-asteroides-planeta-tierra

Un asteroide recién descubierto pasará este jueves muy cerca de la Tierra. 23 de septiembre, 2020. https://www.eluniverso.com/noticias/2020/09/23/nota/7987777/asteroide-recien-descubierto-pasara-este-jueves-muy-cerca-tierra

1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

Tema 1. (30 puntos). Considere la sucesión

$\Big( x_n \Big)_{n=0}^{+ \infty}$

cuya ecuación recursiva es:

$x_n = g(x) = \sqrt{3 + x_{n-1}}$

para n  ∈ Ν

a) ¿Se puede afirmar que ∀x ∈ [1,3], g(x) ∈ [1,3]?

b) Pruebe que g es una función contractiva en el intervalo [1,3] y estime el valor de la constante de Lipschitz (cota de la derivada de g)

c) Realice 5 iteraciones partiendo del dato inicial x₀ =2, y determine el orden de convergencia.

d) Encuentre el valor teórico de x^* al cual converge la sucesión y estime el error absolito en la iteración 5.

e) Realice 5 iteraciones con el método de bisección en el intervalo [1,3] para aproximar el punto fijo de la función g(x).

Rúbrica: literal a (3 puntos), literal b (3 puntos), literal c (10 puntos), literal d (4 puntos), literal e (10 puntos)

---

Referencia: Burden 9Ed. Definición 10.5 p633, Theorem 2.4 P62;
Contracción https://es.wikipedia.org/wiki/Contracci%C3%B3n_(espacio_m%C3%A9trico).
Función lipschitziana https://es.wikipedia.org/wiki/Funci%C3%B3n_lipschitziana

 

1ra Evaluación I Término 2019-2020. 2/Julio/2019. MATG1013

Tema 2. (30 puntos) Un cable en forma catenaria es aquel que cuelga entre dos puntos que no se encuentran sobre la misma línea vertical. Como se muestra en la figura 1, no está sujeta a más carga que su propio peso. Así, su peso en N/m actúa como una carga uniforme por unidad de longitud a lo largo del cable.

En la figura 2, se ilustra un diagrama de cuerpo libre de una sección AB, donde T_A y T_B son las fuerzas de tensión en el extremo.

Con base en los balances de fuerzas horizontal y vertical, se obtiene para el cable el siguiente modelo:

$y = \frac{T_A}{w} cosh \Big( \frac{w}{T_A}x \Big) + y_0 - \frac{T_A}{w}$

Donde la altura y del cable está en función de la distancia x.

Además se tiene que:

$cosh(z) = \frac{e^z+ e^{-z}}{2}$

Utilice el método de Newton-Raphson para hallar el valor del parámetro T_A dado los valores de los parámetros w=12, y₀=6 de modelo que el cable tenga una altura de 15 metros para x=50

Rúbrica: Planteamiento del problema (10 puntos), obtener la derivada (5 puntos), plantear el método (5 puntos), iteraciones (5 puntos), verificar tolerancia (5 puntos)

---

Nota: Todos los temas deben mostrar evidencia del desarrollo del método numérico planteado.

Referencia: Chapra 5Ed Problema 8.17 p219 pdf243. Sears&Zemanski Vol1 12Ed problema 5.63. Cuerda con masa p173. https://es.wikipedia.org/wiki/Catenaria

1ra Evaluación II Término 2018-2019. 10/Noviembre/2018. MATG1013

Tema 4. Para pagar una hipoteca de una casa durante n periodos de tiempo se usa la fórmula:

$P = A\Big(\frac{1-(1+i)^{-n}}{i} \Big)$

En ésta ecuación, P es el valor presente de la casa, A es el valor del pago periódico de la deuda durante n periodos y la tasa de interés por periodo es i.

Suponga que la casa tiene un valor presente de 70000 dólares y deberá ser pagada mediante 1200 dólares mensuales por 25 años (300 meses).

a) Plantee la ecuación

b) Encuentre un intervalo para i donde haya un cambio de signo en la función

c) Aplique el método de Newton