4.3 Trazadores lineales (Splines) grado1 con Python

[ Trazador Lineal ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

1. Trazadores lineales (Splines) grado1

Referencia: Chapra 18.6.1 p525

El concepto de trazador se originó en la técnica de dibujo que usa una cinta delgada y flexible (spline) para dibujar curvas suaves a través de un conjunto de puntos.

La unión más simple entre dos puntos es una línea recta. El método crea un polinomio para cada par de puntos consecutivos en el intervalo, por lo que el resultado será una tabla de polinomios.

Los trazadores de primer grado para un grupo de datos ordenados pueden definirse como un conjunto de funciones lineales.

f_0(x) = f(x_0) + m_0(x-x_0), x_0\leq x\leq x_1

f_1(x) = f(x_1) + m_1(x-x_1), x_1\leq x\leq x_2

…

f_n(x) = f(x_{n-1}) + m_{n-1}(x-x_{n-1}), x_{n-1}\leq x\leq x_n

donde

m_i = \frac{f(x_{i+1}) - f(x_i)}{(x_{i+1}-x_i)}

Observe que la expresión de f(x) para un tramo entre dos puntos es el polinomio de grado 1 realizado con diferencia finita avanzadas o las diferencias divididas.

Las ecuaciones se pueden usar para evaluar la función en cualquier punto entre x₀ y x_n. Al localizar primero el intervalo dentro del cual está el punto, puede seleccionar el polinomio que corresponde a ese tramo.

[ Trazador Lineal ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

2. Ejercicio

Datos de los puntos como ejemplo para el algoritmo

xi = [0.1 , 0.2, 0.3, 0.4]
fi = [1.45, 1.8, 1.7, 2.0]

[ Trazador Lineal ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]

3. Desarrollo analítico

El método con trazadores lineales, permite plantear los bloques necesarios para manejar varios polinomios, uno por cada tramo entre dos puntos dentro del intervalo del problema

0.1 ≤ x≤ 0.2

m_0= \frac{1.8 - 1.45}{0.2-0.1} = 3.5

f_0(x) = 1.45 + 3.5(x-0.1)

0.2 ≤ x ≤ 0.3

m_1= \frac{1.7 - 1.8}{0.3-0.2} = -1

f_1(x) = 1.8 + -1(x-0.2)

0.3 ≤ x ≤ 0.4

m_2= \frac{2 - 1.7}{0.4-0.3} = 3

f_3(x) = 1.7 + 3(x-0.3)

El método permitirá disponer de un punto de partida para trazadores de mayor grado, por ejemplo los cúbicos.

[ Trazador Lineal ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

4. Algoritmo en Python

Los polinomios de cada tramo se almacenan en una tabla, cada uno puede ser utilizado individualmente en su respectivo tramo, por ejemplo para realizar la gráfica de línea entre tramos.

# Trazador (spline) lineal, grado 1
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

def trazalineal(xi,fi):
    n = len(xi)
    x = sym.Symbol('x')
    px_tabla = []
    
    tramo = 1
    while not(tramo>=n):
        # con 1ra diferencia finita avanzada 
        numerador = fi[tramo]-fi[tramo-1]
        denominador = xi[tramo]-xi[tramo-1]
        m = numerador/denominador
        pxtramo = fi[tramo-1] + m*(x-xi[tramo-1])
        px_tabla.append(pxtramo)
        tramo = tramo + 1
        
    return(px_tabla)

# PROGRAMA
# INGRESO , Datos de prueba
xi = [0.1 , 0.2, 0.3, 0.4]
fi = [1.45, 1.8, 1.7, 2.0]
muestras = 10 # entre cada par de puntos

# PROCEDIMIENTO
# Tabla de polinomios por tramos
n = len(xi)
px_tabla = trazalineal(xi,fi)

# SALIDA
print('Polinomios por tramos: ')
for tramo in range(1,n,1):
    print('  x = ['+str(xi[tramo-1])
          +','+str(xi[tramo])+']')
    print(str(px_tabla[tramo-1]))

Se obtiene como resultado:

Polinomios por tramos: 
  x = [0.1,0.2]
3.5*x + 1.1
  x = [0.2,0.3]
-1.0*x + 2.0
  x = [0.3,0.4]
3.0*x + 0.8
>>>

Para añadir la gráfica se añaden las instrucciones para:

evaluar el polinomio en cada tramo
concatenar los resultados de todos los tramos en los vectores xtraza, ytraza.
poner en la gráfica los puntos del problema y las líneas que genera cada polinomio

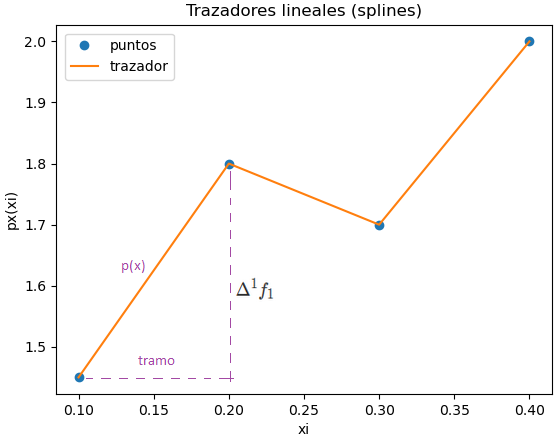
# GRAFICA
# Puntos para graficar cada tramo
xtraza = np.array([])
ytraza = np.array([])
tramo = 1
while not(tramo>=n):
    a = xi[tramo-1]
    b = xi[tramo]
    xtramo = np.linspace(a,b,muestras)

    # evalua polinomio del tramo
    pxtramo = px_tabla[tramo-1]
    pxt = sym.lambdify('x',pxtramo)
    ytramo = pxt(xtramo)

    # vectores de trazador en x,y
    xtraza = np.concatenate((xtraza,xtramo))
    ytraza = np.concatenate((ytraza,ytramo))
    tramo = tramo + 1

# Gráfica
plt.plot(xi,fi,'o', label='puntos')
plt.plot(xtraza,ytraza, label='trazador')
plt.title('Trazadores lineales (splines)')
plt.xlabel('xi')
plt.ylabel('px(xi)')
plt.legend()
plt.show()

[ Trazador Lineal ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]