Ejercicio: 3Eva_IT2003_T5 Calcular área de f(x) por Montecarlo
La forma gráfica del ejercicio permite comprender mejor lo que se estima.
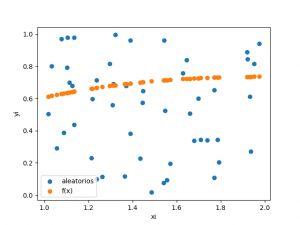Se generan puntos de posiciones aleatorias xi, yi dentro del cuadro limitado por [a,b] en x , [x,d] en y.
Para cada valor de x aleatorio, se evalua en la función f(x), observando si el valor de y aleatorio esta por encima o debajo de la función.
Se estima que la proporción de puntos debajo de f(x) del total de puntos es proporcional al área del rectángulo.
El resultado del algoritmo para un experimento con n = 50 es:
Area estimada: 0.68 Area estimada: 0.62
Se intuye que la precisión mejora al usar n mucho mas grande.
Instrucciones en Python
# 3Eva_IT2003_T5 Calcular área de f(x) por Montecarlo import numpy as np import random as rnd import matplotlib.pyplot as plt # INGRESO n = 50 # puntos aleatorios a = 1 b = 2 fx = lambda x: x*np.exp(-x/2) c = 0 d = 1 # actualizar a max(fx(xi)) # PROCEDIMIENTO xi = [] yi = [] fi = [] bajofx = 0 for i in range(0,n,1): # genera puntos aleatorios unxi = rnd.random()*(b-a)+a unyi = rnd.random()*(d-c)+c fxi = fx(unxi) # debajo de fx() if unyi<=fxi: bajofx = bajofx +1 # guarda los puntos xi.append(unxi) yi.append(unyi) fi.append(fxi) # estima area Arectangulo = (b-a)*(d-c) Aestimada = Arectangulo*bajofx/n # SALIDA print('Area estimada: ', Aestimada) # grafica plt.scatter(xi,yi, label = 'aleatorios') plt.scatter(xi,fi, label = 'f(x)') plt.xlabel('xi') plt.ylabel('yi') plt.legend() plt.show()