Mejoramiento I Término 2003 – 2004. Septiembre 16, 2003 /ICM00794
Nota.- En este examen deben desarrollarse un total de 4 temas. El desarrollo de los temas 1, 2 y 3 es obligatorio. UD. puede seleccionar un solo tema de entre los restantes (4, 5 o 6). Cada tema tiene igual ponderación (25%).
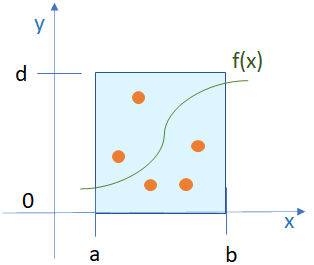
Tema 5. El área bajo la curva de una función f puede estimarse mediante el método de Montecarlo, que consiste en lo siguiente:
- Establecer un rectángulo tal que x Є [a,b]; y Є [0,d], tal que y=f(x)
- Generar un numero n de puntos aleatorios tal que a<x<b, 0<y<d.
- Indicar cuántos de estos puntos caen bajo la curva y=f(x)
- El área bajo la curva puede estimarse mediante la relación:
Escriba un programa en C/C++ que lea las dimensiones a, b, d de la posición del rectángulo, genere aleatoriamente n pares ordenados dentro de ese rectángulo e indique cuántos puntos están bajo la curva y=f(x)=xe-(x/2) en el intervalo [0,2]