LIMITES
En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
Definición rigurosa
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
![]()
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee. Formalmente, utilizando términos lógico-matemáticos:
![]()
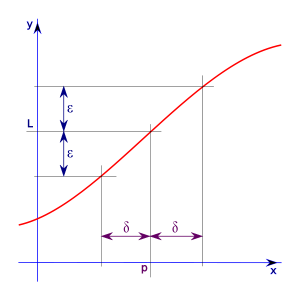
Esta definición se denomina frecuentemente definición épsilon-delta de límite, y se lee como:
«para cada número real ε mayor que cero existe número un real δ mayor que cero tal que, para todo x, si la distancia entre x y c (x no es igual a c) es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε unidades».
Límites notables
Como ejemplo de límites notables tenemos los siguientes límites de funciones, que proveen resultados muy interesantes.
![]()
![]()
![]()
Propiedades de los Limites
Los límites, como otros entes matemáticos, cumplen las siguientes propiedades generales, que son usadas muchas veces para simplificar el cálculo de los mismos.
![]()
Límite por un escalar
![]() donde k es un multiplicador escalar.
donde k es un multiplicador escalar.
Límite de una suma
![]()
Límite de una resta
![]()
Límite de una multiplicación
![]()
Límite de una división
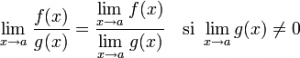
Indeterminaciones
Hay límites que evaluándolos directamente, se obtiene alguna de las siguientes expresiones:
![]()
A estas expresiones se les denomina indeterminaciones, ya que, a simple vista, no está claro cual puede ser el límite (si es que existe). Por ejemplo, en la segunda de estas ecuaciones, el límite pudiese valer 0, 1 o infinito. En algunos casos, simplificando las expresiones u obteniendo expresiones equivalentes a las iniciales, mediante racionalización o factorización se puede resolver la indeterminación y calcular el límite. En otros casos, se requerirá el uso de otras herramientas más potentes como pueden ser las desigualdades o la regla de L’Hopital.
Un ejemplo de indeterminación del tipo es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :
![]()
![]()
![]()
Teoremas de límites
Para facilitar la obtención del límite de una función sin tener que recurrir cada vez a la definición Epsilón-Delta se establecen los siguientes teoremas.
Los teoremas se numeran consecutivamente para facilitar una futura referencia.
Nota: los teoremas se presentan sin demostración, pero quien quiera verla puede hacer clic en el vínculo correspondiente.
Teorema de límite1:
Si k es una constante y a un número cualquiera, entonces
![]()
Teorema de límite2:
Para cualquier número dado a,
![]()
Teorema de límite3:
Si m y b son dos constantes cualesquiera, entonces
![]()
Teorema de límite4:
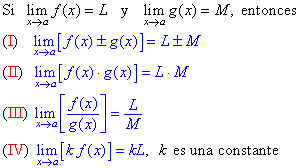
Teorema de límite5:

Teorema de límite6:
Si f es un polinomio y a es un número real, entonces
![]()
Teorema de límite7:
Si q es una función racional y a pertenece al dominio de q, entonces
![]()
Teorema de límite8:

Procedimiento para calcular límites
Si es posible aplicar directamente las propiedades anteriores, el límite se calcula directamente. Con respecto a las propiedades, como la propiedad 6 se aplica a cualquier polinomio y las propiedades 1, 2, 3, y 4 implican funciones polinómicas es indistinto que nos refiramos a cada una de las propiedades 1 a 4 en particular que a la propiedad 6 cuando calculamos el límite de una función polinómica. Lo mismo, la propiedad 7 se aplica a una función racional y la propiedad 4 (III) también.
Cuando al sustituir la a por x en la función nos da la forma indeterminada 0/0 es posible calcular el límite pero, previamente, hay que transformar la fórmula de la función de tal modo que, una vez hecha la simplificación pertinente, se pueda evitar la división por cero: para lograr esto disponemos de procedimientos algebraicos eficaces como la factorización, la conjugada, etc.
Ejercicios resueltos
Evalué los siguientes límites indicando la propiedad o propiedades que se aplican en cada paso:

Límites unilaterales
Hay casos en que las funciones no están definidas (en los reales) a la izquierda o a la derecha de un número determinado, por lo que el límite de la función cuando x tiende a dicho número, que supone que existe un intervalo abierto que contiene al número, no tiene sentido.
Ejemplo:

Límite unilateral por la derecha:
Sea f una función definida en todos los números del intervalo abierto (a, c). Entonces, el límite de f (x), cuando x se aproxima a a por la derecha es L, y se escribe
![]()
Límite unilateral por la izquierda:
Sea f una función definida en todos los números de (d, a). Entonces, el límite de f (x), cuando x se aproxima a a por la izquierda es L, y se escribe
![]()
Limite Bilateral
![]()
Teorema de límite12:
![]()
Ejercicios resueltos
En los ejercicios 1 a 4, trace la gráfica y determine el límite indicado si existe; si no existe, dé la razón:

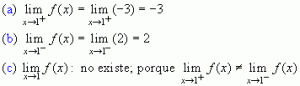
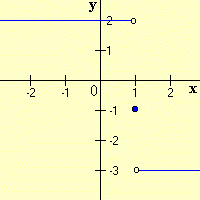
Los siguientes ejercicios quedan para que los lectoras procedan a realizarlos, cualquier consultan pueden comunicarse enviando un mail a: luchegas@hotmail.com (autor de este blog)
Límites infinitos
Existen ciertas funciones que aumentan o disminuyen sin límite a medida que la variable independiente se acerca a un valor fijo determinado.
Crecimiento infinito:

Decrecimiento infinito:
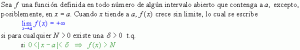
Teorema de límite13:
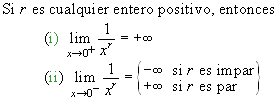
Teorema de límite14:

Teorema de límite15:
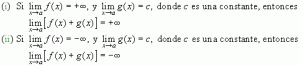
Teorema de límite16:
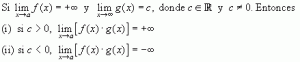
Teorema de lìmite 17:
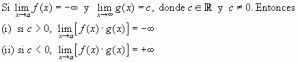
Una asíntota es una recta a la cual se aproxima una curva indefinidamente. Trazar las asíntotas, tanto verticales como horizontales (más adelante nos ocuparemos de estas últimas), es de gran ayuda para dibujar la gráfica de una función.
Asíntota vertical:
Una asíntota vertical es una recta paralela al eje y.
Se dice que la recta x = a es una asíntota vertical de la gráfica de la función f si por lo menos uno de los siguientes enunciados es verdadero:
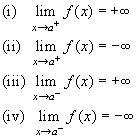
Ejercicios resueltos y por resolver
En los ejercicios 1 a 7, determine el límite. En los ejercicios 9 a 11. encuentre la(s) asíntota(s) vertical(es) de la gráfica de la función y trácela(s).

Solución del ejercicio 1.

Solución del ejercicio 2.

Límites en el infinito
Teorema de límite18:
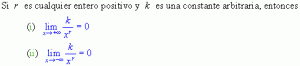
Asíntota horizontal:
Una asíntota horizontal es una recta paralela al eje x.

Teorema de límite19:
![]()
Continuidad de una función

Criterios de continuidad de una función en un número
Se dice que una función f es continua en el número a si y sólo si se cumplen las tres condiciones siguientes:
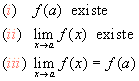
Una función que no es continua en un número, se dice que es discontinua en dicho número. En la gráfica de una función que es discontinua en el número a se puede observar un «salto» o un «hueco» precisamente donde x = a. La discontinuidad puede ser eliminable o esencial.
![]()
Las discontinuidades eliminables se denominan también discontinuidad de «hueco»: en la gráfica de las funciones donde sucede este caso se puede ver un «hueco» en el punto del plano cuyas coordenadas son (a, f (a)).
Las discontinuidades esenciales también reciben los nombres de discontinuidad de «salto»: se presenta cuando los límites unilaterales existen pero son diferentes; y, la discontinuidad infinita sucede cuando el límite de f cuando x tiende a a es infinito.
Teoremas de continuidad












holaaaaa