3Eva2016TI_T2 LTI CT Sub-sistemas h(t) multiplicados con Fourier

3ra Evaluación I Término 2016-2017. 15/septiembre/2016 TELG1001

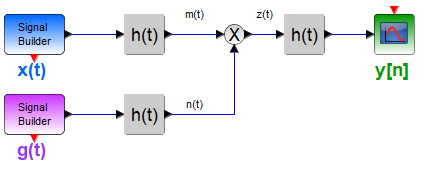
Tema 2. (26 puntos) Considere el sistema mostrado en la siguiente figura, donde la respuesta impulso h(t) está dada por:

h(t) = \frac{\sin (11 \pi t)}{\pi t}

x(t) = \sum_{k=1}^{\infty} \frac{1}{k^2} \cos (5k \pi t) g(t) = \sum_{k=1}^{10} \cos (8k \pi t)

a. Determinar la energía contenida en la señal h(t)

b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal m(t). Es decir M(ω) vs ω.

c. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal n(t). Es decir N(ω) vs ω.

d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.

---

Coordinador: Tama Alberto