Para usar el simulador con diagrama de bloques para respuesta a impulso unitario, es necesario usar la expresión:
h(t) = b_0 \delta (t) +P(D)[y_n(t) \mu(t)]Donde si el orden de P(D) es menor al orden de Q(D) entonces b0=0.
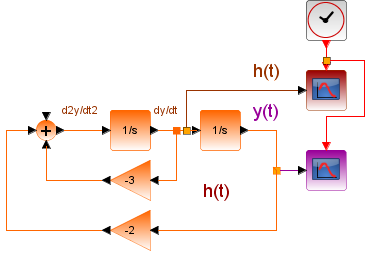
Para el ejercicio desarrollado en el sistema modelo, P(D)=D, por lo que hay una sola derivada, que se puede obtener de la entrada del primer integrador de y(t).
( D^2 + 3D +2 ) y(t) = Dx(t)Para obtener h(t), el impulso unitario x(t), es semejante a tener una condicion inicial sin señal de entrada, siguiendo la teoría descrita de sobre condiciones iniciales.
El impulso unitario representa que y'(t) inicia con 1, por ser el término de más alto orden en P(D) y se configura el diagrama de bloques:
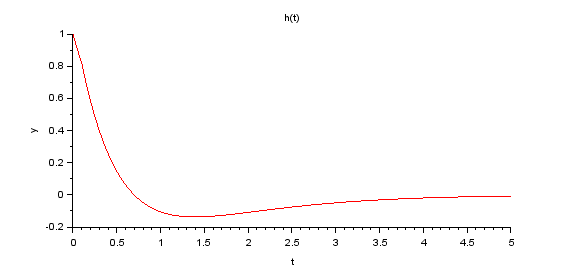
Con lo que la respuesta del sistema al impulso unitario que se obtiene es:
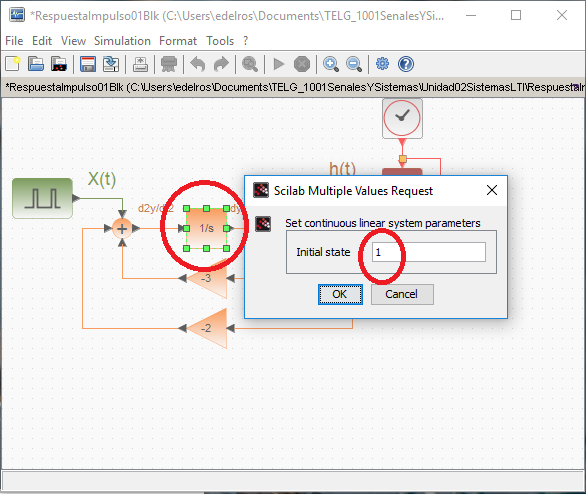
El parámetros inicial se configuró en:
Como referencia para observación se muestra la salida y(t):
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]