Ejercicio: 1Eva2009TII_T3 LTI CT y(t) desde h(t) y x(t) con términos escalón desplazados
La función de transferencia h(t) y la señal de entrada x(t) son,
x(t) = 2 μ(t-1) – 2 μ(t-3)
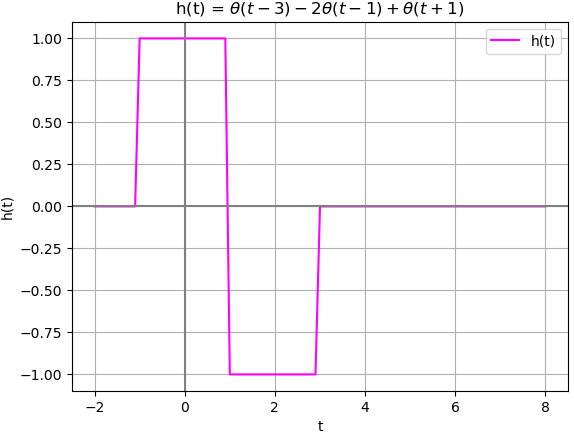
h(t) = μ(t+1) – 2 μ(t-1) + μ(t-3)
La primera observación es que h(t) h(t) tiene un componente No causal, que se adelanta en tiempo μ(t+1) a x(t). La transformada unilateral de Laplace no aplica para este término, por lo que para el algoritmo se usa la entrada X(s) y se evita el error en la transformada. Por lo demás el algoritmo funciona bien.
Tarea: Revisar y justificar
Usando la función de transferencia h(t) con las transformadas de Laplace H(s)
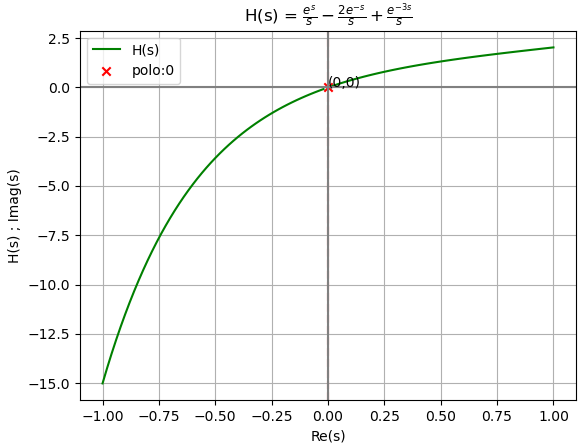
H(s) = \frac{1}{s}e^{s} - 2\frac{1}{s}e^{-s}+ \frac{1}{s} e^{-3s}simplificando la expresión como F(s)*(terminos exponenciales)
H(s) = \frac{1}{s} \Big[ e^{s} - 2e^{-s}+ e^{-3s} \Big]tiene la forma gráfica,
La señal de entrada usando las transformadas de Laplace X(s)
X(s) = 2\frac{1}{s}e^{-s} - 2\frac{1}{s}e^{-3s} X(s) = \frac{2}{s} \Big[e^{-s} - e^{-3s} \Big]La señal de salida Y(s)=H(s)*X(s)
Y(s) = \frac{2}{s^2} \Big[ e^{s} - 2e^{-s}+ e^{-3s} \Big] \Big[e^{-s} - e^{-3s} \Big]multiplicando los términos de exponenciales
Y(s) = \frac{2}{s^2} \Big[ e^{s}e^{-s} - 2e^{-s}e^{-s}+ e^{-3s}e^{-s} - e^{s}e^{-3s} + 2e^{-s}e^{-3s} - e^{-3s}e^{-3s} \Big] Y(s) = \frac{2}{s^2} \Big[ 1 - 2e^{-2s}+ e^{-4s}- e^{-2s} + 2e^{-4s} - e^{-6s} \Big] Y(s) = \frac{2}{s^2} \Big[ 1 - 3e^{-2s}+ 3e^{-4s} - e^{-6s} \Big]usando la tabla de transformadas de Laplace en forma inversa:
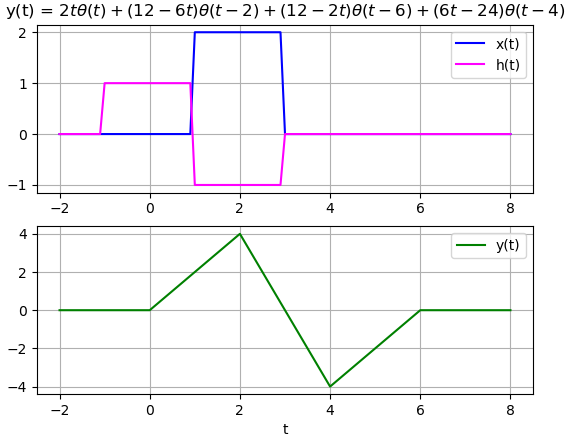
y(t) = 2 (t) \mu (t) -6 (t-2) \mu (t-2) +6(t-4) \mu (t-4) -2(t-6) \mu(t-6) \Big]La respuesta al impulso H(s)no tiene polos en el lado derecho del plano s, por lo que las salidas son acotadas, en consecuencia el sistema es asintoticamente estable y también BiBO estable.
usando el algoritmo, considerando que las condiciones iniciales son cero,:
H(s) = P(s)/Q(s):
s -s -3*s
e 2*e e
-- - ----- + -----
s s s
H(s) en factores:
s -s -3*s
e 2*e e
-- - ----- + -----
s s s
h(t) :
Heaviside(t - 3) - 2*Heaviside(t - 1) + Heaviside(t + 1)
polosceros:
exp(s) : {'Q_polos': {0: 1}, 'P_ceros': {}, 'Hs_k': 1/s}
exp(-3*s) : {'Q_polos': {0: 1}, 'P_ceros': {}, 'Hs_k': 1/s}
exp(-s) : {'Q_polos': {0: 1}, 'P_ceros': {}, 'Hs_k': -2/s}
Q_polos : {0: 1}
P_ceros : {}
Estabilidad de H(s):
n_polos_real : 0
n_polos_imag : 1
enRHP : 0
unicos : 0
repetidos : 0
asintota : estable
X(s):
-s -3*s
2*e 2*e
----- - -------
s s
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0
ZSR respuesta estado cero:
ZSR :
-2*s -4*s -6*s
2 6*e 6*e 2*e
-- - ------- + ------- - -------
2 2 2 2
s s s s
yt_ZSR :
2*t*Heaviside(t) + (12 - 6*t)*Heaviside(t - 2) + (12 - 2*t)*Heaviside(t - 6) +
(6*t - 24)*Heaviside(t - 4)
Y(s)_total = ZIR + ZSR:
-2*s -4*s -6*s
2 6*e 6*e 2*e
-- - ------- + ------- - -------
2 2 2 2
s s s s
y(t)_total = ZIR + ZSR:
2*t*Heaviside(t) + (12 - 6*t)*Heaviside(t - 2) + (12 - 2*t)*Heaviside(t - 6) +
(6*t - 24)*Heaviside(t - 4)
>>>
Usando los bloques desarrollados en la y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta.
# Y(s) Respuesta total con entada cero y estado cero # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # http://blog.espol.edu.ec/telg1001/ import sympy as sym import matplotlib.pyplot as plt import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) d = sym.DiracDelta(t) u = sym.Heaviside(t) # H(s) respuesta impulso Hs = sym.exp(s)/s - 2*sym.exp(-s)/s + sym.exp(-3*s)/s # X(s) Señal de entrada xt = 2*u.subs(t,t-1) - 2*u.subs(t,t-3) # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [0] # estado cero no se usan # Grafica, intervalo tiempo [t_a,t_b] t_a = -2 ; t_b = 8 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO Hs = fcnm.apart_s(Hs) # fracciones parciales Hs_fc = fcnm.factor_exp(Hs) # en factores Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc) polosceros = fcnm.busca_polosceros(Hs) Q_polos = polosceros['Q_polos'] P_ceros = polosceros['P_ceros'] estable = fcnm.estabilidad_asintotica_s(Q_polos) # H(t) respuesta al impulso ht = 0*s term_suma = sym.Add.make_args(Hs) for term_k in term_suma: ht_k = sym.inverse_laplace_transform(term_k,s,t) # simplifica log(exp()) ej: e**(-2s)/(s**2) if ht_k.has(sym.log): ht_k = sym.simplify(ht_k,inverse=True) ht = ht + ht_k lista_escalon = ht.atoms(sym.Heaviside) ht = sym.expand(ht,t) # terminos suma ht = sym.collect(ht,lista_escalon) # PROCEDIMIENTO Respuesta ZIR, ZSR Xs = fcnm.laplace_transform_suma(xt) # ZIR_s respuesta entrada cero de s sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio) ZIR = sol_ZIR['ZIR'] yt_ZIR = sol_ZIR['yt_ZIR'] # ZSR respuesta estado cero, Y(s) a entrada X(s) sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs) ZSR = sol_ZSR['ZSR'] yt_ZSR = sol_ZSR['yt_ZSR'] # Respuesta total Y(s) y y(t) Ys = ZIR + ZSR Ys = fcnm.apart_s(Ys) yt = yt_ZIR + yt_ZSR lista_escalon = yt.atoms(sym.Heaviside) yt = sym.collect(yt,lista_escalon) # SALIDA print(' H(s) = P(s)/Q(s):') sym.pprint(Hs) print(' H(s) en factores:') sym.pprint(Hs_fc) if len(Hs_Qs2)>0: print('\nH(s) parámetros cuadraticos:') fcnm.print_resultado_dict(Hs_Qs2) print('\n h(t) :') sym.pprint(ht) print('\npolosceros:') fcnm.print_resultado_dict(polosceros) print('\nEstabilidad de H(s):') for k in estable: print('',k,':',estable[k]) print('\n X(s): ') sym.pprint(Xs) print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales') if not(sol_ZIR == sym.nan): # existe resultado fcnm.print_resultado_dict(sol_ZIR) else: print(' insuficientes condiciones iniciales') print(' revisar los valores de cond_inicio[]') print('\n ZSR respuesta estado cero:') fcnm.print_resultado_dict(sol_ZSR) print('\n Y(s)_total = ZIR + ZSR:') sym.pprint(Ys) print('\n y(t)_total = ZIR + ZSR:') sym.pprint(yt) # Graficas polos, H(s), con polos h(t) -------- muestras_H = 101 figura_s = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,f_nombre='H',solopolos=True) figura_Hs = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,muestras=muestras_H,f_nombre='H') figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h') # GRAFICAS y(t),x(t),h(t) --------------------- figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras) plt.show()