Referencia: 1Eva2009TII_T5 LTI DT bloques H[z] en serie
1. Las respuestas impulso de cada subsistema
H_1[z] = \frac{z}{z-(0.7)} = \frac{z}{z-0.7}usando la tabla de transformadas z
h_1[n] = (0.7)^n \mu[n]Continuando con el subsistema de la derecha
H_2[z] = \frac{z}{z-(-0.5)} = \frac{z}{z+0.5} h_2[n] = (-0.5)^n \mu[n]El sistema total:
H[z] = H_1[z] H_2[z] = \frac{z}{(z-0.7)} \frac{z}{(z+0.5)} = \frac{z^2}{(z-0.7)(z+0.5)}fracciones parciales modificadas, multiplica ambos lados por 1/z
\frac{H[z]}{z} = \Big( \frac{1}{z} \Big) \frac{z^2}{(z-0.7)(z+0.5)}= \frac{z}{(z-0.7)(z+0.5)} \frac{H[z]}{z} = \frac{z}{(z-0.7)(z+0.5)} = \frac{k_1}{z-0.7} +\frac{k_2}{z+0.5} k_1 = \frac{z}{\cancel{(z-0.7)}(z+0.5)} \Big|_{z=0.7} = \frac{0.7}{(0.7+0.5)} = 0.5833 k_2 = \frac{z}{(z-0.7)\cancel{(z+0.5)}} \Big|_{z=-0.5} = \frac{-0.5}{(-0.5-0.7)} = 0.4166 \frac{H[z]}{z} = \frac{0.5833}{z-0.7} +\frac{0.4166}{z+0.5}Restaura fracciones parciales, multiplica ambos lados por z
H[z] = \frac{0.5833 z}{z-0.7} +\frac{0.4166z}{z+0.5}usando la tabla de transformadas z
h[n] = 0.5833 \Big(0.7 \Big)^n \mu[n] +0.4166 \Big(-0.5\Big)^n \mu[n]factor común μ[n]
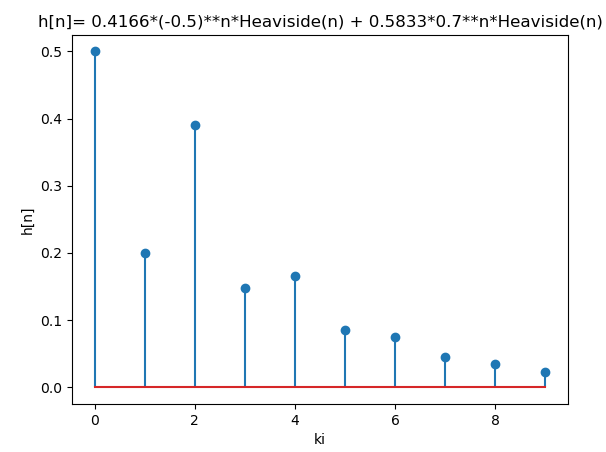
h[n] = \Bigg( 0.5833 \Big(0.7 \Big)^n +0.4166 \Big(-0.5\Big)^n \Bigg) \mu[n]Revisando el resultado con el algoritmo en Python
Hz:
2
z
-------------------
(z - 0.7)*(z + 0.5)
Hz/z:
z
---------------------
2
1.0*z - 0.2*z - 0.35
Hz/z.apart:
0.416666666666667 0.583333333333333
----------------- + -----------------
1.0*z + 0.5 1.0*z - 0.7
Hz = (Hz/z)*z
0.416666666666667*z 0.583333333333333*z
------------------- + -------------------
1.0*z + 0.5 1.0*z - 0.7
polos: {-0.500000000000000: 1, 0.700000000000000: 1}
polos Re: [-1/2, 7/10]
Tarea: 2. Su respuesta y[n]=s]n], expresada a la mínima expresión frente a la siguiente excitación x[n]=μ[n], esquematícela.
Instrucciones en Python
Algoritmos desarrollados en X[z] Fracciones parciales modificadas con Python
y la parte gráfica de Transformada z con Sympy-Python
# Transformada z- Fracciones parciales # Polos únicos, repetidos y complejos # Lathi Ejercicio 5.3c pd495 # blog.espol.edu.ec/telg1001 import sympy as sym import numpy as np import matplotlib.pyplot as plt # INGRESO z = sym.Symbol('z') Pz = z**2 Qz = (z-0.7)*(z+0.5) # PROCEDIMIENTO P = Pz.as_poly(z) Q = Qz.as_poly(z) Xz = Pz/Qz # Raices Denominador Q_raiz = sym.roots(Q) Q_raizRe = sym.real_roots(Q) rcompleja = len(Q_raiz)-len(Q_raizRe) # Raices reales, únicas y repetidas if (rcompleja<=0 and len(Q_raizRe)>0): # fracciones parciales modificadas Xzz = (P/Q)/z Xzm = Xzz.apart() # fracciones parciales restaurada terminos = Xzm.args Xzp = 0*z for untermino in terminos: Xzp = Xzp + untermino*z def parametro_cuadratico(untermino): unparametro ={} # revisa denominador cuadratico [numerador,denominador] = (untermino).as_numer_denom() gradoD = 0 coeficientesD = denominador gradoN = 0 coeficientesN = numerador if not(denominador.is_constant()): denominador = denominador.as_poly() gradoD = denominador.degree() coeficientesD = denominador.coeffs() if not(numerador.is_constant()): numerador = numerador.as_poly() gradoN = numerador.degree() coeficientesN = numerador.coeffs() if gradoD == 2 and gradoN==2: a = float(coeficientesD[1])/2 gamma2 = float(coeficientesD[2]) gamma = np.sqrt(gamma2) A = float(coeficientesN[0]) B = float(coeficientesN[1]) rN = (A**2)*gamma2 + B**2 - 2*A*a*B rD = gamma2 - a**2 r = np.sqrt(rN/rD) beta = np.arccos(-a/gamma) thetaN = A*a-B thetaD = A*np.sqrt(gamma2-a**2) theta = np.arctan(thetaN/thetaD) unparametro = {'r':r, 'gamma':gamma, 'beta':beta, 'theta':theta} return (unparametro) # Terminos cuadraticos parametros = [] # denominador cuadratico if (rcompleja>0 and len(Q_raizRe)>0): # fracciones parciales modificadas Xzz = (P/Q)/z Xzm = Xzz.apart() # fracciones parciales restaurada terminos = Xzm.args Xzp = 0*z for untermino in terminos: Xzp = Xzp + untermino*z unparam = parametro_cuadratico(untermino*z) if len(unparam)>0: parametros.append(unparam) if (rcompleja>0 and len(Q_raizRe)==0): Xzp = P/Q parametros.append(parametro_cuadratico(P/Q)) # SALIDA print('\n Hz:') sym.pprint(Xz) if (len(Q_raizRe)>0): print('\n Hz/z:') sym.pprint(Xzz) print('\n Hz/z.apart:') sym.pprint(Xzm) print('\n Hz = (Hz/z)*z') sym.pprint(Xzp) print('\n polos: ', Q_raiz) print('\n polos Re: ', Q_raizRe) if len(parametros)>0: for unparam in parametros: print('parametros cuadraticos: ') for cadauno in unparam.keys(): print(cadauno,'\t',unparam[cadauno]) # grafica plano z imaginario figura, grafROC = plt.subplots() # limite radio1 = plt.Circle((0,0),1,color='lightgreen', fill=True) radio2 = plt.Circle((0,0),1,linestyle='dashed', color='lightgreen',fill=False) grafROC.add_patch(radio1) for raiz in Q_raiz.keys(): [r_real,r_imag] = raiz.as_real_imag() radio_raiz = np.abs(raiz) nROC = plt.Circle((0,0),radio_raiz, color='red',fill=True) grafROC.add_patch(nROC) grafROC.add_patch(radio2) # borde r=1 grafROC.axis('equal') # marcas de r=1 y valor a for raiz in Q_raiz.keys(): [r_real,r_imag] = raiz.as_real_imag() grafROC.plot(r_real,r_imag,'o',color='orange', label ='polo:'+str(float(raiz))+';'+str(Q_raiz[raiz])) grafROC.plot(1,0,'o',color='green', label ='radio:'+str(1)) plt.axhline(0,color='grey') plt.axvline(0,color='grey') plt.grid() plt.legend() plt.xlabel('Re[z]') plt.ylabel('Imag[z]') untitulo = 'ROC H[z]='+str(Xz) plt.title(untitulo) # h[n] usando tabla de transformadas m = 10 n = sym.Symbol('n') hn = 0.5833*((0.7)**n)*sym.Heaviside(n)+0.4166*((-0.5)**n)*sym.Heaviside(n) fn = sym.lambdify(n,hn) ki = np.arange(0,m,1) xnk = fn(ki) # grafica h[n] figura, grafxn = plt.subplots() plt.stem(ki,xnk) plt.xlabel('ki') plt.ylabel('h[n]') plt.title('h[n]= '+str(hn)) plt.show()