… [ señal de energía ] [ señal de potencia ]
Señal de Energía
Referencia: Lathi 1.1-1 p65, Hsu 1.2.G p5
Una señal de energía tiene energía finita. En general toda señal en el sentido práctico tiene duración finita, por lo que la energía es finita.
La energía se define como:
E=\int_{-\infty}^{\infty} x^2(t) dto de una forma más general incluyendo señales de tipo compleja:
E=\int_{-\infty}^{\infty} |x(t)|^2 dtNo se considera solo como energía el área bajo la curva, o integral de la señal, debido a que puede contener áreas de signo negativo que pueden cancelar la media. El cuadrado de la señal será siempre positivo.
La señal tiene que ser de tipo finita para que la medida tenga significado. Una condición necesaria para que la señal sea finita es que su amplitud → 0 cuando |t|→ ∞. En cualquier otro caso la integral no converge.
Para una señal discreta:
E=\sum_{n=-\infty}^{\infty} | x[n] |^2Ejemplo de señal de Energía
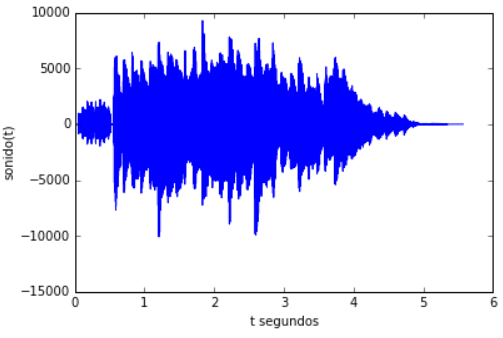
Un ejemplo de señal de Energía es un audio limitado en el tiempo, pues su amplitud tiende a 0 cuando |t|→ ∞.
Usando el mismo archivo de audio del ejercicio de señales analógicas y digitales:
Recuerde que el archivo de audio.wav debe estar en el mismo directorio de trabajo que el archivo algoritmo.py.
El audio mostrado es una señal limitada en el tiempo, por lo que es posible calcular su energía usando la formula descrita.
Referencia: Archivos de Audio.wav – Abrir, extraer una porción en CCPG1001 Fundamentos de programación
para procesar el archivo, las instrucciones en Python son:
# Señales de Energía y Potencia import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves # INGRESO # archivo = input('archivo de audio: ') archivo = 'Alarm01.wav' # PROCEDIMIENTO muestreo, sonido = waves.read(archivo) muestra = len(sonido) dt = 1/muestreo t = np.arange(0,muestra*dt,dt) uncanal = sonido[:,0] # SALIDA - Observación intermedia plt.plot(t,uncanal) plt.xlabel('t segundos') plt.ylabel('sonido(t)') plt.show()
Integración numérica de muestras
En el caso de las muestras disponibles de audio, las muestras están igualmente espaciadas, se puede integrar usando la regla de Simpson´s integrate.simps(valores,t) para obtener un estimado de alta precisión.
Para desarrollar el tema de integración numérica puede revisar el tema en Métodos numéricos en el siguiente enlace: Unidad 05 Integración y Diferenciación Numérica
import scipy.integrate as integrate # cuadrado de la señal para el integral de energía cuadrado = uncanal**2 #integrando a partir de muestras de la señal energia = integrate.simps(cuadrado,t) # SALIDA print(' La energía del audio es: ',energia) print('\n revisando el canal y sus cuadrados') print(uncanal[2500:2510]) print(cuadrado[2500:2510])
La energía del audio es: 3827.5753288 revisando el canal y sus cuadrados [-16 -1 8 -3 -8 4 11 -1 -4 10] [256 1 64 9 64 16 121 1 16 100]
[ señal de energía ] [ señal de potencia ]
…
Señal de Potencia
Si en x(t) la amplitud no tiende → 0 al mismo tiempo que |t|→ ∞, la energía de la señal será infinita.
Una mejor medida de la señal en este caso es promedio de energía en el un intervalo de tiempo T, si es periódica, existe T.
La señal de potencia se define como:
P_x =\lim_{T \to \infty}\frac{1}{T} \int_{-T/2}^{T/2} | x(t) |^2 dty para una señal discreta:
P =\lim_{N \to \infty}\frac{1}{2N+1} \sum_{n=-N}^{N} | x[n] |^2Ejemplo: potencia de una señal
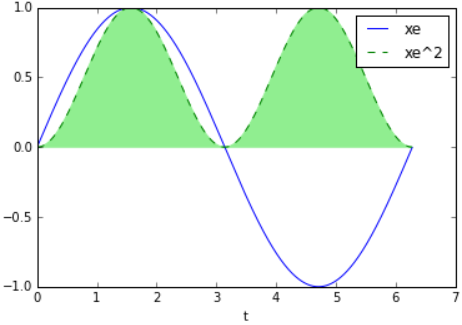
Considere una señal periódica conocida sin(), integrando dentro de un periodo podemos calcular la energía y luego la potencia.
# Señales de Energía y Potencia import numpy as np import matplotlib.pyplot as plt import scipy.integrate as integrate # INGRESO - Parámetros w = 1 fx = lambda t: np.sin(w*t) a = 0 b = 2*np.pi # un periodo T dte = 0.005 # PROCEDIMIENTO T = 2*np.pi/w te = np.arange(a,b,dte) xe = fx(te) # energía en un periodo cuadradoxe = xe**2 energiaxe = integrate.simps(cuadradoxe,te) # potencia en un periodo potenciaxe = (1/T)*energiaxe # SALIDA print('la energia de xe es: ',energiaxe) print('la potencia de xe es: ',potenciaxe) # gráfica plt.plot(te,xe,label='xe') plt.fill_between(te,0,cuadradoxe,color='lightgreen') plt.plot(te,cuadradoxe,'g--', label='xe^2') plt.xlabel('t') plt.legend() plt.show()
la energia de xe es: 3.14159264282 la potencia de xe es: 0.499999998285
Para revisar los resultados, realizamos el cálculo de potencia haciendo x(t)=sin(t)
P_x =\lim_{T \to \infty}\frac{1}{T} \int_{-T/2}^{T/2} | x(t) |^2 dtse tiene que:
=\frac{1}{2\pi} \int_{0}^{2\pi} | sin(t) |^2 dt = \frac{1}{2\pi} \int_{0}^{2\pi} \Big[ \frac{1}{2}-\frac{cos(2t)}{2}\Big] dt =\frac{1}{4\pi} \int_{0}^{2\pi} \Big[ 1-{cos(2t)}\Big] dt =\frac{1}{4\pi} \Big[\int_{0}^{2\pi} 1 dt - \int_{0}^{2\pi}{cos(2t)} \Big]dt =\frac{1}{4\pi} \Big[t \Big|_0^{2\pi} \ - \frac{sin(2x)}{2}\Big|_0^{2\pi} \ \Big] =\frac{1}{4\pi}\Big[(2\pi-0)- (sin(2\pi)-sin(0)) \Big] = \frac{1}{2}que es el resultado de potencia obtenido usando Python.
Tarea
Realice el mismo cálculo para la energía de la señal del ejemplo anterior.