Referencia: Oppenheim 1.3.2 fig.1.25 p24, Lathi 1.3.1 p78, Hsu 1.2.A p1
Las señales discretas tienen un dominio que se especifica únicamente para valores finitos de tiempo, generalmente definidos con números enteros. Por ejemplo, para una señal discreta en un intervalo desde n0, con m muestras, tamaño de paso 1, se genera una secuencia numérica cuya gráfica es:
\sin [\omega n]El muestreo para cada valor n se establece en el intervalo [0, m) , para m muestras y con frecuencia ω = 2π/12 radianes/segundo.
Para el ejercicio se usa m=12
Semejante a las gráficas de señales contínua, el bloque de INICIO añade las librerías de Numpy y Matplotlib.
El bloque de INGRESO define los valores de los parámetros, la señal f(x) en formato simplificado lambda, con variable independiente n, el punto inicial n0 y el número de muestras m (recuerde contar el cero)
# Señales discretas import numpy as np import matplotlib.pyplot as plt # INGRESO - parámetros w = 2*np.pi/12 fx = lambda n: np.sin(w*n) n0 = 0 # intervalo en un periodo muestras = 12+1
En el bloque de Procedimiento, los valores discretos de n se almacenan en un vector de tamaño m. La señal se puede crear usando la función sin() incluida en numpy.
# PROCEDIMIENTO # vector ni discreto [n0,n0+muestras] ni = np.arange(n0,n0+muestras,1) senal = fx(ni)
Observe que los valores para n corresponden a una secuencia numérica.
El bloque de SALIDA puede mostrar los resultados en forma numérica o gráfica.
# SALIDA np.set_printoptions(precision=4) print('n: ') print(ni) print('señal x[n]: ') print(senal)
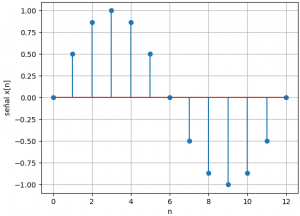
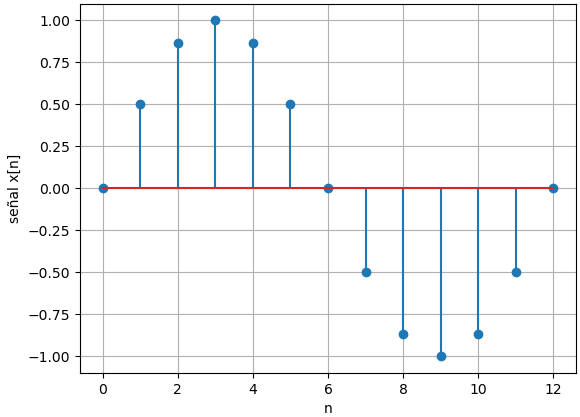
n: [ 0 1 2 3 4 5 6 7 8 9 10 11 12] señal x[n]: [ 0.0000e+00 5.0000e-01 8.6603e-01 1.0000e+00 8.6603e-01 5.0000e-01 1.2246e-16 -5.0000e-01 -8.6603e-01 -1.0000e+00 -8.6603e-01 -5.0000e-01 -2.4493e-16]
Para observar el resultado de la señal, se grafica ni vs señal[n], añadiendo las etiquetas para cada eje, y mostrando el resultado con plt.show().
Se usa la gráfica stem() para obtener en la gráfica el punto y una línea que muestre la magnitud, semejante a las gráficas de los libros de texto.
# Gráficas plt.stem(ni, senal) plt.xlabel('n') plt.ylabel('señal x[n]') plt.grid() plt.show()
Tarea
Para ésta sección, se cambiarán los parámetros de n y ω.
- muestras = 50
- ω0 = π/4 y ω0 = 15π/8
- cambiar la función a np.cos()
- ¿se puede cambiar la amplitud de la señal a 2 y ω0=1/6?
Instrucciones Python
# Señales discretas import numpy as np import matplotlib.pyplot as plt # INGRESO - parámetros w = 2*np.pi/12 fx = lambda n: np.sin(w*n) n0 = 0 # intervalo [n0,n0+muestras] muestras = 12+1 # PROCEDIMIENTO # vector n de muestras [n0,n0+muestras] ni = np.arange(n0,n0+muestras,1) senal = fx(ni) # SALIDA np.set_printoptions(precision=4) print('n: ') print(ni) print('señal x[n]: ') print(senal) # Gráficas plt.stem(ni, senal) plt.xlabel('n') plt.ylabel('señal x[n]') plt.grid() plt.show()