Referencia: Oppenheim 1.2.1 p8 pdf39, Lathi 1.2-1 p71
[ desplazamiento ] [ escalamiento ] [ inversión ] en el dominio tiempo
Desplazamiento en tiempo de señales
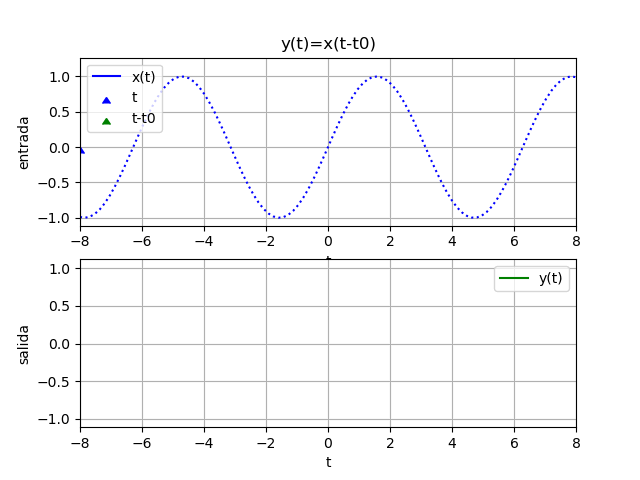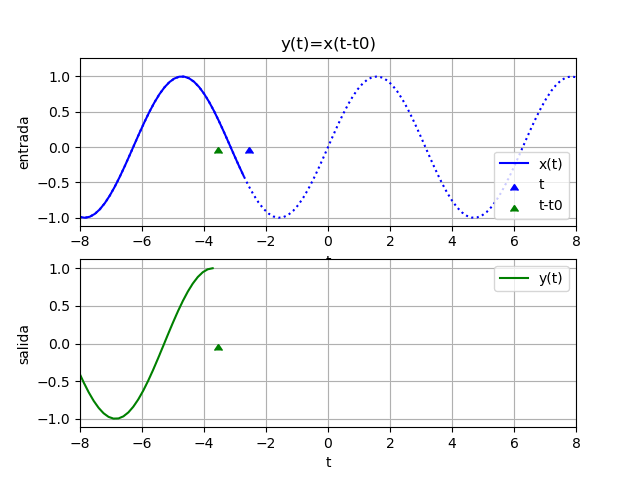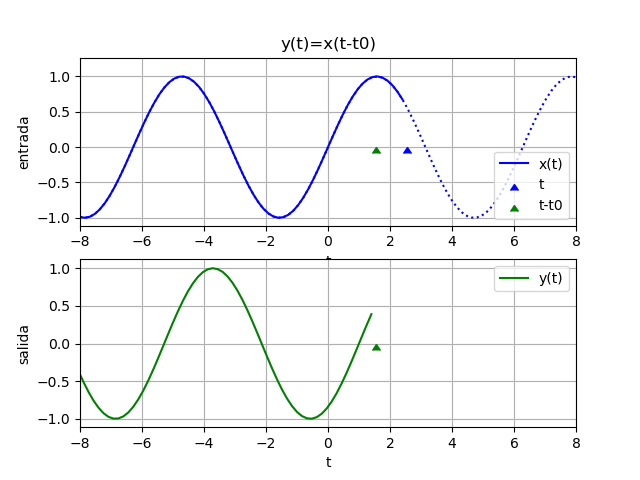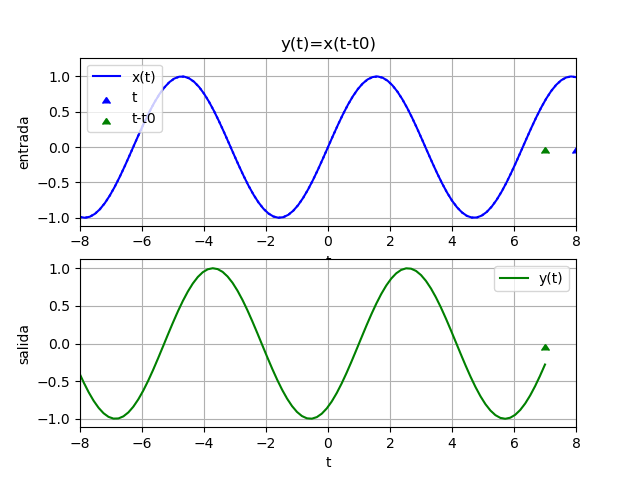
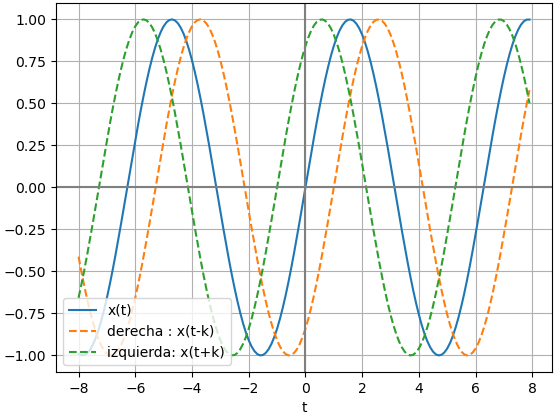
Una señal x(t) que se retrasa por k segundos se representa como una versión desplazada hacia la derecha el eje t.
Es decir:
\phi (t+k)= x(t)o de otra forma:
\phi (t)= x(t-k)se podrá observar entonces que el signo determina el desplazamiento hacia:
- la derecha si se resta k
- la izquierda si se suma k
Para mostrar las reglas, se tiene el siguiente ejemplo, usando como señal
x(t)=sen(t)Instrucciones en Python
# Señales- Operaciones import numpy as np import matplotlib.pyplot as plt # INGRESO w = 1 fx = lambda t: np.sin(w*t) k = 1 # desplazamiento # intervalo de tiempo [a,b) a = -8 b = 8 dt = 0.1 # PROCEDIMIENTO ti = np.arange(a,b,dt) senal = fx(ti) derecha = fx(ti-k) izquierda = fx(ti+k) # SALIDA plt.figure(1) plt.plot(ti,senal,label='x(t)') plt.plot(ti,derecha, label='derecha : x(t-k)', linestyle='dashed') plt.plot(ti,izquierda, label='izquierda: x(t+k)', linestyle='dashed') plt.axvline(0, color='gray') plt.axhline(0, color='gray') plt.xlabel('t') plt.legend(loc='lower left') plt.grid() plt.show()
[ desplazamiento ] [ escalamiento ] [ inversión ] en el dominio tiempo
..
Escalamiento en tiempo de señales
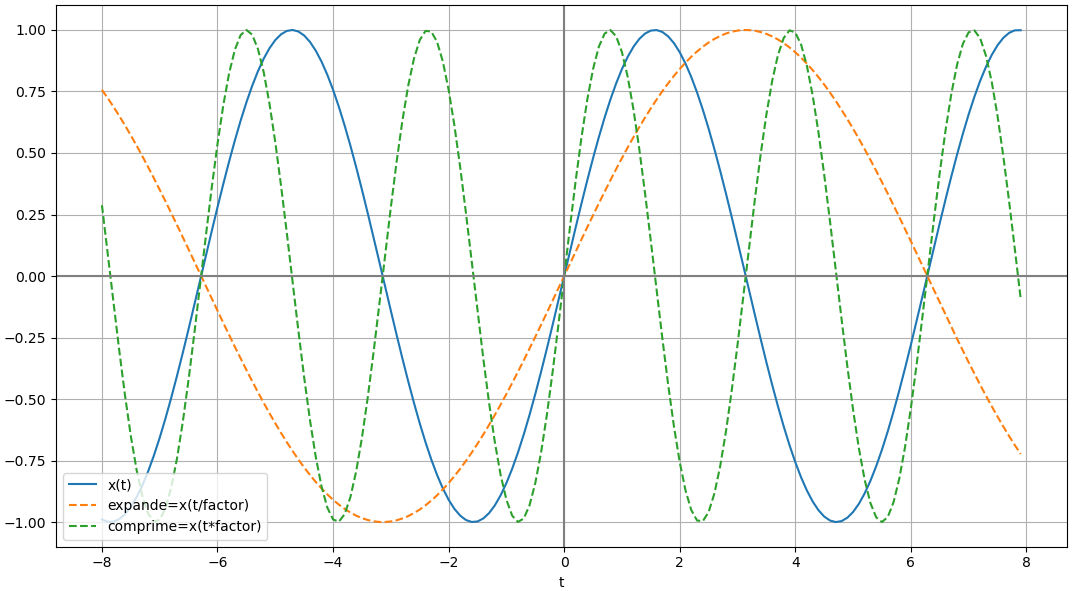
La compresión o expansión de la señal en el tiempo es conocida como escalamiento en el tiempo.
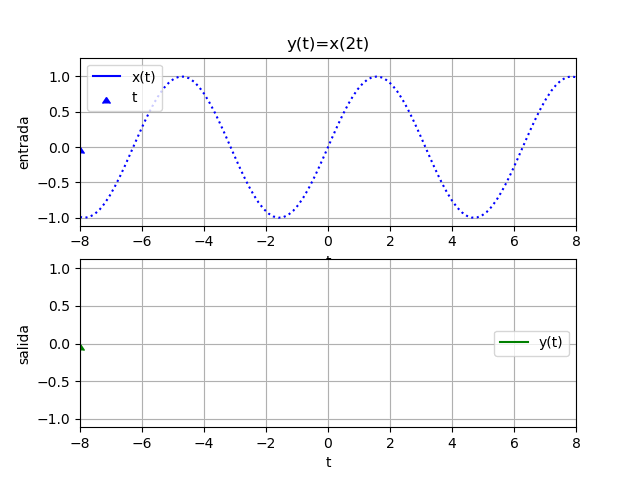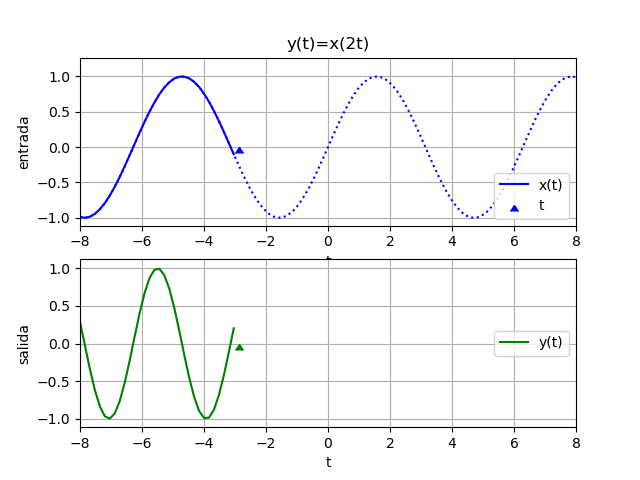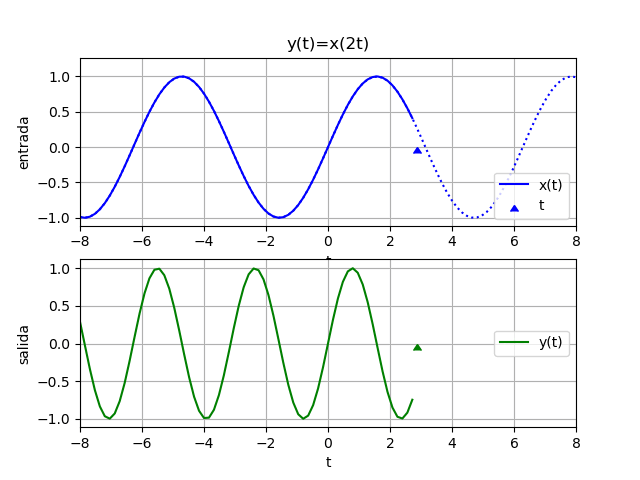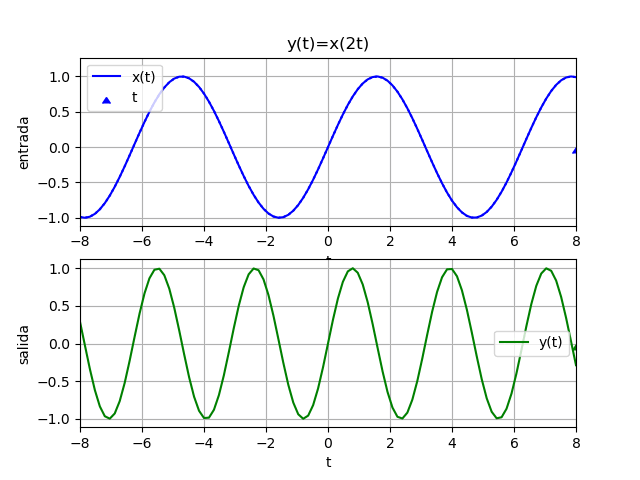
Considere la señal x(t) afectada en el tiempo por un factor de 2.
Se encuentra que:
siguiendo con la señal del ejercicio anterior
x(t) = sin(t)# Escalamiento en tiempo factor = 2 expande = fx(ti/factor) comprime = fx(factor*ti) # GRAFICA expande o comprime plt.figure(2) plt.plot(ti,senal,label='x(t)') plt.plot(ti,expande, label='expande=x(t/factor)', linestyle='dashed') plt.plot(ti,comprime, label='comprime=x(t*factor)', linestyle='dashed') plt.axvline(0, color='gray') plt.axhline(0, color='gray') plt.xlabel('t') plt.legend(loc='lower left') plt.grid() plt.show()
[ desplazamiento ] [ escalamiento ] [ inversión ] en el dominio tiempo
Inversión en tiempo de una señal
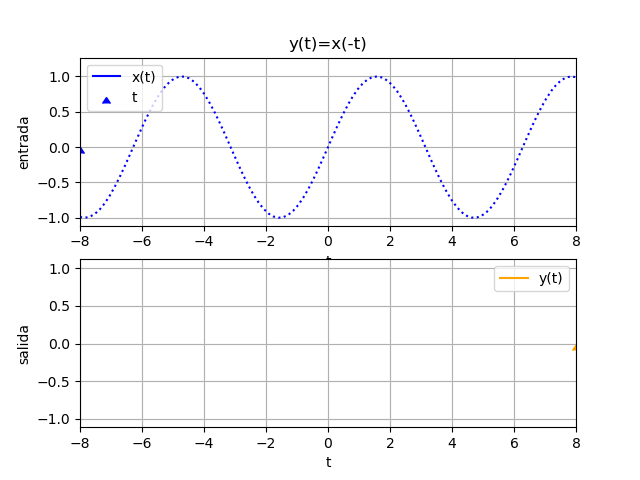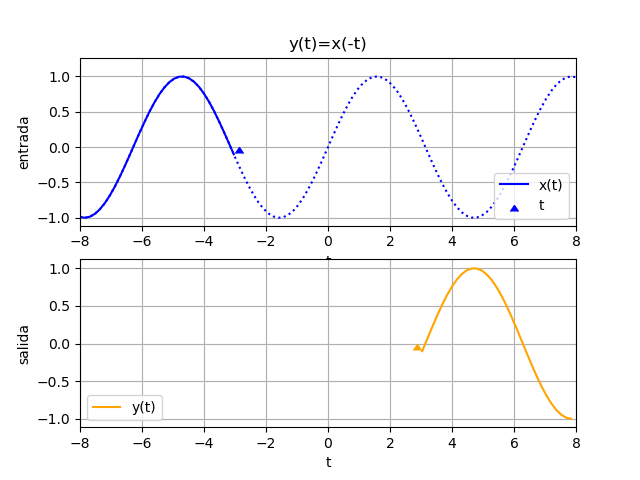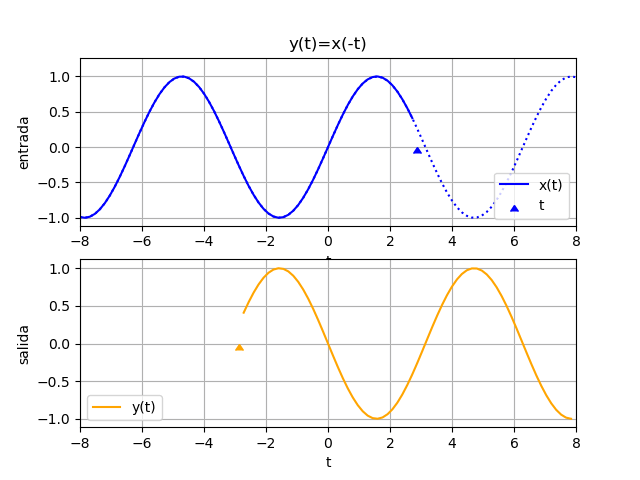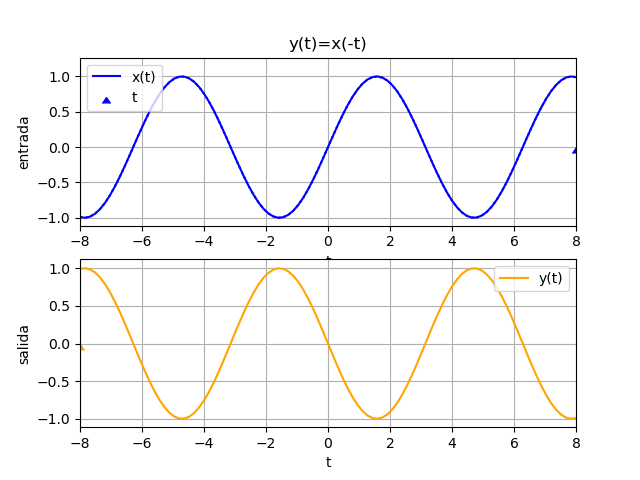
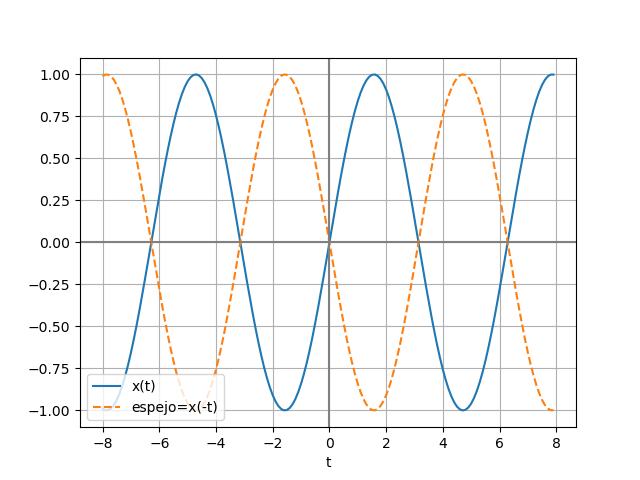
Si la función resultante es x(-t), la señal x(t) se invierte rotando sobre el eje de las ordenadas (vertical).
\phi (t)= x(-t)Observe el resultado de la ecuación de ejemplo:
# inversion en tiempo espejo = fx(-ti) # SALIDA plt.figure(3) plt.plot(ti,senal,label='x(t)') plt.plot(ti,espejo, label='espejo=x(-t)', linestyle='dashed') plt.axvline(0, color='gray') plt.axhline(0, color='gray') plt.xlabel('t') plt.legend(loc='lower left') plt.grid() plt.show()
[ desplazamiento ] [ escalamiento ] [ inversión ] en el dominio tiempo
Modelo general de desplazamiento, escalamiento, e inversión
En resumen, el efecto de transformar la variable independiente de una señal x(t) para obtener la señal modificada es de la forma:
x(at+b)Con la transformación, la variable independiente conserva la forma de x(t). La señal puede ser:
- alargada linealmente cuando |a| < 1 ,
- comprimida si |a| > 1,
- invertida en el tiempo si a < 0, y
- desplazada en el tiempo si b es diferente de cero.
- siendo desplazada a la derecha si se resta el valor de |b|
- siendo desplazada a la izquierda si se suma el valor de |b|
Ejemplo de desplazamiento en tiempo de una señal
Observe por un minuto el siguiente video sobre el desplazamiento en el tiempo (delay) en una guitarra.
[ desplazamiento ] [ escalamiento ] [ inversión ] en el dominio tiempo