Referencia: Lathi 1.5 p92, Oppenheim 1.2.3 p13 pdf44, Hsu 1.2.E p3
Señales Pares
Una función o señal x(t) ó x[n] es par si se «refleja» en el eje vertical u ordenadas, es decir tienen simetría reflectiva a través del eje de las y.
x(t) = x(-t) x[n] = x[-n]La señal tiene los mismos valores para el lado positivo o negativo de |t|. Es como si se aplicara el valor absoluto de t antes de aplicarlo en la ecuación.
Señales Impares
La gráfica de una función o señal impar es simétrica con respecto al origen. Una señal x(t) ó x[n] es impar si se cumple que:
x(t) = -x(-t) x[n] = -x[-n]Una señal impar debe ser necesariamente 0 en t=0 o n=0.
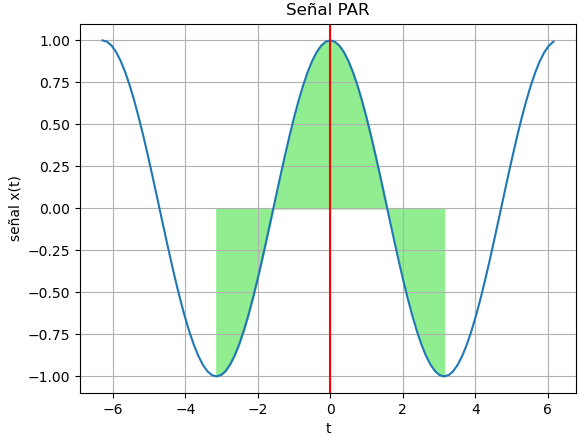
Ejemplo de gráfica de función o señal par con Python
Un señal par conocida es cos(t). Para observar mejor, se marcará el área que genera la función dentro de un periodo centrado en el origen. Para ilustrar mejor el concepto se reutiliza los ejemplos anteriores de señales periódicas.
Se inicializa los parámetros para:
- el periodo T de una señal
- el número m de periodos que se observarán de la señal, donde m debe ser un número par.
- El punto de inicio t0 para el eje horizontal se puede calcular a partir de T y m, dado que se extiende hacia cada lado del eje vertical, t0 al encontrarse a la izquierda del eje vertical tiene signo negativo.
- El punto de final tn para tendrá el signo positivo de t0
- los tramos por periodo de la señal a observar, deben ser un número 2k, donde k es un número entero.
# Señales pares e impares import numpy as np import matplotlib.pyplot as plt # INGRESO parámetros T = 2*np.pi f = 1/T w = 2*np.pi*f fx = lambda t: np.cos(w*t) m = 2 # incluir m periodos en grafica t0 = -(m/2)*T # usa lado negativo de abscisas tramos = 32 # tramos por periodo 2**k, siendo k entero
Para observar mejor la gráfica, se marcará el área que genera la señal dentro de un periodo centrado en el origen.
La cantidad de muestras depende de cuántos periodos m de la señal se quieran observar. Se necesitan tantas muestras como tramos de cada lado, incluyendo la muestra del origen (m*tramos+1).
# PROCEDIMIENTO tn = -t0 # vector de tiempo muestras = m*tramos+1 ti = np.linspace(t0,tn,muestras) # dt = ti[1]-ti[0] dt = (tn-t0)/(tramos*m) senal = fx(ti) # marcar un periodo en [desde, hasta] desde = -T/2 hasta = desde + T + dt tperiodo = np.arange(desde,hasta,dt) periodo = fx(tperiodo)
Se marca un periodo comprendido en: [-T/2,T/2], sombreando alrededor de t=0. Para destacar el eje vertical se usa el color rojo.
# SALIDA # Gráficas plt.plot(ti,senal) plt.xlabel('t') plt.ylabel('señal x(t)') plt.grid(True) # marcar un periodo plt.title('Señal PAR') plt.fill_between(tperiodo,0,periodo, color='lightgreen') plt.axvline(x=0, color='red') plt.show()
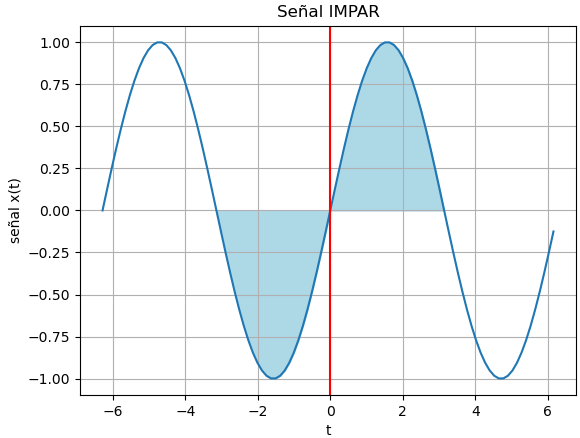
Ejemplo de gráfica de función o señal impar con Python
En el ejemplo se usará una señal par como el sin(). Se utiliza las instrucciones del algoritmo anterior, modificando la señal f(x) en el bloque de ingreso
fx = lambda t: np.sin(w*t)
y el título de la gráfica
plt.title('Señal IMPAR')
Las instrucciones en Python para señales pares e impares son:
# Señales pares e impares import numpy as np import matplotlib.pyplot as plt # INGRESO parámetros T = 2*np.pi f = 1/T w = 2*np.pi*f fx = lambda t: np.cos(w*t) m = 2 # incluir m periodos en grafica t0 = -(m/2)*T # usa lado negativo de abscisas tramos = 32 # tramos por periodo 2**k, siendo k entero # PROCEDIMIENTO tn = -t0 # vector de tiempo muestras = m*tramos+1 ti = np.linspace(t0,tn,muestras) # dt = ti[1]-ti[0] dt = (tn-t0)/(tramos*m) senal = fx(ti) # marcar un periodo en [desde, hasta] desde = -T/2 hasta = desde + T + dt tperiodo = np.arange(desde,hasta,dt) periodo = fx(tperiodo) # SALIDA # Gráficas plt.plot(ti,senal) plt.xlabel('t') plt.ylabel('señal x(t)') plt.grid(True) # marcar un periodo plt.title('Señal PAR') plt.fill_between(tperiodo,0,periodo, color='lightgreen') plt.axvline(x=0, color='red') plt.show()
Tarea
probar con otras funciones tales como:
- t
- |t|
- t2
- t3
- |- et|
nota: el valor absoluto en Python para t se escribe como abs(t), o usando numpy np.abs(t)