Señal [ sinusoidal ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
1. Señales Sinusoidales
La forma general de una señal sinusoidal en el dominio del tiempo se obtiene por medio de su argumento de una función coseno de variable independiente t.
x(t) = A\cos(\omega_0 t +\phi) = A\cos(2\pi f_0 t +\phi)por lo que se deduce que:
\omega_0 = 2\pi f_0se desatacan tres parámetros independientes: Amplitud (A), fase (φ), frecuencia angular (ω) en radianes o la frecuencia por ciclos (f) en Hz.
Señal [ sinusoidal ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
2. Ejercicio
Referencia: McClellan ejemplo 2.1 p35, Downey 1.1 p2.
Para la señal definida por x(t) mostrar los parámetros de Amplitud, Frecuencia y Fase.
x(t) = 20 \cos(2\pi(40)t - 0.4\pi)Señal [ sinusoidal ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
3. Desarrollo analítico
Por observación de x(t) según los conceptos definiciones en la parte teórica:
x(t) = A\cos(\omega_0 t +\phi)los parámetros buscados son:
Amplitud A = 20
ω0 = 2 π(40) rad/s
f0 = 40 Hz
φ = -0.4π rad.
El tamaño vertical de la señal en el tiempo depende del parámetro Amplitud, su máximo y mínimo +20 a -20.
El tiempo de entre máximos sucesivos es de 0.025 s, que es 1/f0 .
Señal [ sinusoidal ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
4. Algoritmo con Sympy
Cuando para x(t) se requiere obtener sus parámetros o características, se usa la forma simbólica con las herramientas de la librería Sympy.
Luego de hacer el llamado a Sympy, procede a indicar la variable independiente de tiempo 't' para ser reconocida como un símbolo. También se pueden añadir constantes como π o 2π para facilitar la escritura de la expresión x(t):
# ejemplo 2.1 p35 cos_args grafica senoidal # telg1034 DSP fiec-espol edelros@espol.@espol.edu import sympy as sym # variables continuas t = sym.Symbol('t', real=True,nonnegative=True) # t>=0 pi = sym.pi DosPi = sym.UnevaluatedExpr(2*sym.pi)
La expresión x(t) se escribe usando los símbolos definidos en el ejercicio.
# INGRESO
x = 20*sym.cos(DosPi*40*t-0.4*pi)
Como la expresión x(t) es simple y tiene un patrón Amplitud*cos(Freq_rad*t+Fase), se separan sus partes con la instrucción x.args. La separación de argumentos se realiza con expresiones de sumas de términos, factores multiplicadores o argumentos de una función como el cos().
# PROCEDIMIENTO
amplitud = 1; freq_rad = 0; fase = 0
partes = x.args
El resultado de las partes es una tupla. La Amplitud corresponde a la parte que no tiene sym.cos, el resto debería ser el la parte del coseno. Si la expresión contiene mas de dos partes, se analiza la expresión iterando en cada parte.
parte_cos = sym.S.Zero # busca cos(t) for unaparte in partes: if not(unaparte.has(sym.cos)): amplitud = partes[0] else: parte_cos = unaparte
La expresión interna de cos(Freq_rad*t+Fase) se obtiene también como el argumento tupla de un solo elemento, obtenida como parte_cos.args[0].
# revisa cos(freq_rad*t+fase)
argumento_cos = parte_cos.args[0]
Los términos de la suma se revisan uno por uno, La frecuencia angular se obtiene como el término que tiene símbolo 't', que al dividir para 't' y se obtiene el valor en en radianes. La revisión contenido de t en un término se realiza por medio untermino.has(t), La fase es el término sin el símbolo 't'.
terminos_suma = argumento_cos.args for untermino in terminos_suma: if untermino.has(t): freq_rad = sym.simplify(untermino/t) freq_Hz = sym.simplify(freq_rad/(2*pi)) else: fase = untermino
La instrucción sym.simplify() permite simplificar los valores como π al calcular freq_Hz
El bloque de resultados muestra en orden los valores obtenidos durante el proceso
# SALIDA print('x(t): ') sym.pprint(x) print('\npartes o argumentos') print('partes : ', partes) print('parte_cos: ',parte_cos) print('argumento_cos: ',argumento_cos) print('términos_suma: ', terminos_suma) print('\nparámetros') print('amplitud: ',amplitud) print('freq_rad: ',freq_rad) print('freq_Hz : ',freq_Hz) print('fase : ',fase)
los resultados se presentan a continuación:
x(t): 20*cos(40*t*2*pi - 0.4*pi) partes o argumentos partes : (20, cos(40*t*(2*pi) - 0.4*pi)) parte_cos: cos(40*t*(2*pi) - 0.4*pi) argumento_cos: 40*t*(2*pi) - 0.4*pi términos_suma: (-0.4*pi, 40*t*(2*pi)) parámetros amplitud: 20 freq_rad: 80*pi freq_Hz : 40 fase : -0.4*pi >>>
Instrucciones en Python
# ejemplo 2.1 p35 parámetros de x(t) # telg1034 DSP fiec-espol edelros@espol.edu.ec import sympy as sym # variables continuas t = sym.Symbol('t', real=True,nonnegative=True) # t>=0 pi = sym.pi DosPi = sym.UnevaluatedExpr(2*sym.pi) # INGRESO x = 20*sym.cos(DosPi*40*t-0.4*pi) # PROCEDIMIENTO amplitud = 1; freq_rad = 0; fase = 0 partes = x.args parte_cos = sym.S.Zero # busca cos(t) for unaparte in partes: if not(unaparte.has(sym.cos)): amplitud = partes[0] else: parte_cos = unaparte # revisa cos(freq_rad*t+fase) argumento_cos = parte_cos.args[0] terminos_suma = argumento_cos.args for untermino in terminos_suma: if untermino.has(t): freq_rad = sym.simplify(untermino/t) freq_Hz = sym.simplify(freq_rad/(2*pi)) else: fase = untermino # SALIDA print('x(t): ') sym.pprint(x) print('\npartes o argumentos') print('partes : ', partes) print('parte_cos: ',parte_cos) print('argumento_cos: ',argumento_cos) print('términos_suma: ', terminos_suma) print('\nparámetros') print('amplitud: ',amplitud) print('freq_rad: ',freq_rad) print('freq_Hz : ',freq_Hz) print('fase : ',fase)
[ ejercicio ] [ analítico ] [ algoritmo ] [ tarea ]
..
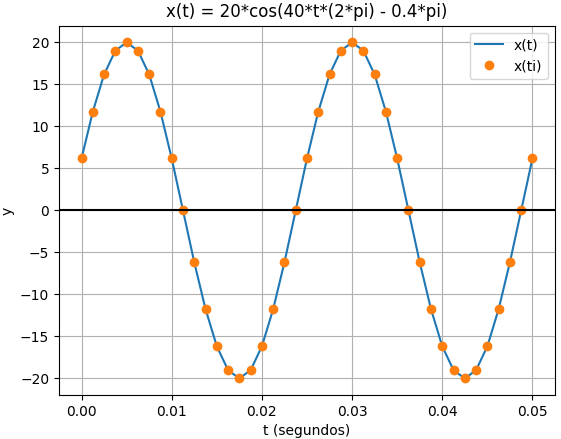
5. Gráfica de la señal sinusoidal
Para realizar la gráfica de la función se debe añadir las librerías para los cálculos (Numpy) y la librería para realizar la gráfica (Matplotlib)
# GRAFICAR x(t) --------------------------- import numpy as np import matplotlib.pyplot as plt
Como parámetros de la función periódica se puede indicar el número de periodos a mostrar en la gráfica. Recordando que el periodo T es el inverso de la frecuencia f en Hz.
# INGRESO muestreo_T = 20+1 # tramos+1, o pasos+1 graf_periodos = 2 # periodos en una grafica
Como la gráfica básica realiza un muestreo de la señal y luego une los puntos con rectas, para observar una curva «suave» se usaría un muestreo de unos 20 tramos o 21 muestras por periodo.
Las muestras de tiempo ti se obtienen con los datos de [a,b] y dt usando la instrucción np.arange().
Para la evaluación de x(t) en el intervalo con el vector ti es preferible usar la forma numérica (lambda) que usa todo el vector ti en una sola instrucción. La forma de evaluación de Sympy es con xt.subs() y sería con valores individuales. Se realiza la conversión de Sympy a Numpy usando la instrucción sym.lambdify(variable, expresión). (lambfify en resumen de sympy)
# x(t) a forma numérica lambda t: xt = sym.lambdify(t,x) xi = xt(ti) # evalúa en intervalo
Para revisar o recordar los detalles de la creación de la gráfica con plt.plot(), puede revisar lo indicado en los enlaces siguientes:
Señales Contínuas con Python (curso: Señales y Sistemas)
Gráficas 2D de línea (curso: Fundamentos de Programación)
Observación: Para la gráfica se requieren valores numéricos reales (float) en los vectores [ti,xi]. Si la expresión de x(t) aún no se definen los valores de los parámetros, la sección de la gráfica mostraría un error. Considerar para el próximo algoritmo.
Instrucciones en Python
# GRAFICAR x(t) --------------------------- import numpy as np import matplotlib.pyplot as plt # INGRESO muestreo_T = 20+1 # tramos+1, o pasos+1 periodos_graf = 2 # periodos en una grafica # PROCEDIMIENTO GRAFICA T = 1/freq_Hz a = 0 # [a,b] intervalo ti b = T*periodos_graf dt = T/(muestreo_T-1) # tamaño de paso,tramo, muestreo ti = np.arange(a,b+dt,dt,dtype=float) # x(t) a forma numérica lambda t: xt = sym.lambdify(t,x) xi = xt(ti) # evalúa en intervalo # graficar plt.plot(ti,xi,label='x(t)') plt.plot(ti,xi,'o',label='x(ti)') plt.axhline(0,color='black') plt.xlabel('t (segundos)') plt.ylabel('y') plt.title('x(t) = ' + str(x)) plt.legend() plt.grid() plt.show()
Señal [ sinusoidal ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]
..
6. Tarea
Usar el algoritmo con los siguientes ejercicios y observar las diferencias al usar Sympy al determinar los parámetros. Crear nuevos Símbolos de ser necesario
x = 10*sym.cos(2*pi*440*t-0.4*pi) x = 10*sym.cos(DosPi*440*t-0.4*pi) x = 20*sym.cos(DosPi*40*t-0.4*pi) x = 4*sym.cos(40*pi*t+pi/3) x = A*sym.sin(w*t+p)
Señal [ sinusoidal ] [ ejercicio ] [ analítico ] [ algoritmo ] [ gráfica ]