Referencia: Oppenheim 1.1 p1 pdf32, Lathi 1.3.1 p78, Hsu 1.2.A p1
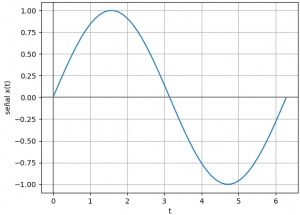
Un ejemplo clásico de una señal contínua es una de forma sinusoidal.
\sin (\omega t)La función de la señal en el tiempo se define en el intervalo [t0, tn) para n tramos y una frecuencia angular ω en radianes/segundo. Recordar que ω = 2πf, siendo f la frecuencia en Hz o unidades de 1/s, por si requiere hacer la conversión de frecuencias.
Para facilitar la tarea, en Python se usan las librerías para el manejo de vectores y gráficas:
-
- vectores – numpy
- gráficas – matplotlib.pyplot
Un resumen de gráficas en 2D de línea se presenta también en el curso MATG1052 de métodos numéricos. También se dispone de un video tutorial: Funciones y Gráficas .
Inicio e Ingreso de parámetros
En el bloque de INICIO se añaden las librerías Numpy y Matplotlib. Luego se definen los parámetros de la señal a usar y se describe la señal con la expresión matemática en su forma simplificada lambda.
Se añade el intervalo de observación y el número de muestras para la gráfica.
# Señales continuas import numpy as np import matplotlib.pyplot as plt # INGRESO w = 1 fx = lambda t: np.sin(w*t) t0 = 0 # intervalo [t0,tn] tn = 2*np.pi muestras = 51
Procedimiento – calcular valores
Para la gráfica, las muestras de tiempo t se almacenan en un vector de tamaño n. Entre cada valor de t existe una diferencia dt determinada por n.
# PROCEDIMIENTO # vector de tiempo ti = np.linspace(t0,tn,muestras) # señal senal = fx(ti)
Salida – valores y gráfica
El resultado puede ser observado de dos formas:
– mostrando sus valores o
– sus gráficas.
Se presentan las dos opciones a escoger.
# SALIDA np.set_printoptions(precision = 4) print('tiempo: ') print(ti) print('señal: x(t) ') print(senal)
tiempo: [0. 0.1257 0.2513 0.377 0.5027 0.6283 0.754 0.8796 1.0053 1.131 1.2566 1.3823 1.508 1.6336 1.7593 1.885 2.0106 2.1363 2.2619 2.3876 2.5133 2.6389 2.7646 2.8903 3.0159 3.1416 3.2673 3.3929 3.5186 3.6442 3.7699 3.8956 4.0212 4.1469 4.2726 4.3982 4.5239 4.6496 4.7752 4.9009 5.0265 5.1522 5.2779 5.4035 5.5292 5.6549 5.7805 5.9062 6.0319 6.1575] señal: x(t) [ 0.0000e+00 1.2533e-01 2.4869e-01 3.6812e-01 4.8175e-01 5.8779e-01 6.8455e-01 7.7051e-01 8.4433e-01 9.0483e-01 9.5106e-01 9.8229e-01 9.9803e-01 9.9803e-01 9.8229e-01 9.5106e-01 9.0483e-01 8.4433e-01 7.7051e-01 6.8455e-01 5.8779e-01 4.8175e-01 3.6812e-01 2.4869e-01 1.2533e-01 -3.2162e-16 -1.2533e-01 -2.4869e-01 -3.6812e-01 -4.8175e-01 -5.8779e-01 -6.8455e-01 -7.7051e-01 -8.4433e-01 -9.0483e-01 -9.5106e-01 -9.8229e-01 -9.9803e-01 -9.9803e-01 -9.8229e-01 -9.5106e-01 -9.0483e-01 -8.4433e-01 -7.7051e-01 -6.8455e-01 -5.8779e-01 -4.8175e-01 -3.6812e-01 -2.4869e-01 -1.2533e-01]
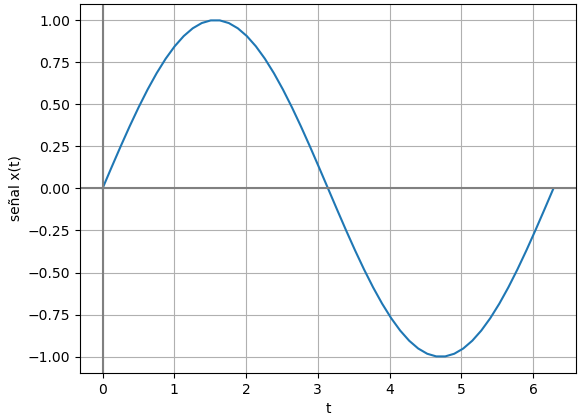
Para observar el resultado de la señal, se grafica t vs señal. Para mejor identificación de ejes, se añade las etiquetas y las líneas de referencia.
# Gráfica plt.plot(ti,senal) plt.axhline(0, color='gray') plt.axvline(0, color='gray') plt.xlabel('t') plt.ylabel('señal x(t)') plt.grid() plt.show()
Tarea
Para ésta sección, se cambiarán los parámetros de tiempo.
- tn=8π
- ω=2
- cambiar la función a
np.cos() - ¿se puede cambiar la amplitud de la señal a 4?
Instrucciones en Python
# Señales continuas import numpy as np import matplotlib.pyplot as plt # INGRESO w = 1 fx = lambda t: np.sin(w*t) t0 = 0 # intervalo [t0,tn] tn = 2*np.pi muestras = 51 # PROCEDIMIENTO # vector de tiempo ti = np.linspace(t0,tn,muestras) # señal senal = fx(ti) # SALIDA np.set_printoptions(precision = 4) print('tiempo: ') print(ti) print('señal: x(t) ') print(senal) # Gráfica plt.plot(ti,senal) plt.axhline(0, color='gray') plt.axvline(0, color='gray') plt.xlabel('t') plt.ylabel('señal x(t)') plt.grid() plt.show()