[ periodo ] [ desplazamiento ] [ ejercicio ] [ algoritmo ] [ gráfica ] [_telg1034.py _as_dsp ]
..
1. Periodo de x(t)
Referencia: McClellan 2.3.1 p35, 2.3.2 p37
El periodo T0 de una sinusoidal es el tiempo que dura un ciclo de la señal. La frecuencia en Hz determina su periodo, es decir que al aplicar un desplazamiento de T0, se repite la misma señal.
T_0 = \frac{2\pi}{\omega_0} = \frac{1}{f_0} x(t+T_0) = x(t)2. Desplazamiento en tiempo de x(t)
El efecto de aplicar a t un desplazamiento t0 diferente al periodo T0, presenta un desfase de adelanto o retraso según el signo de t0 como se muestra en la gráfica. Siendo x(t) = A cos(ωt)
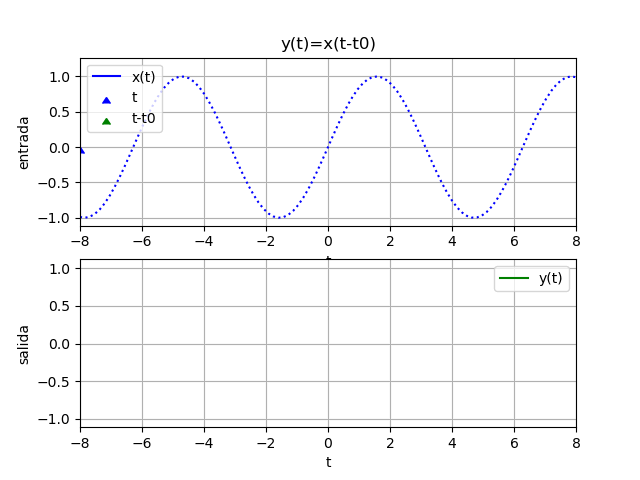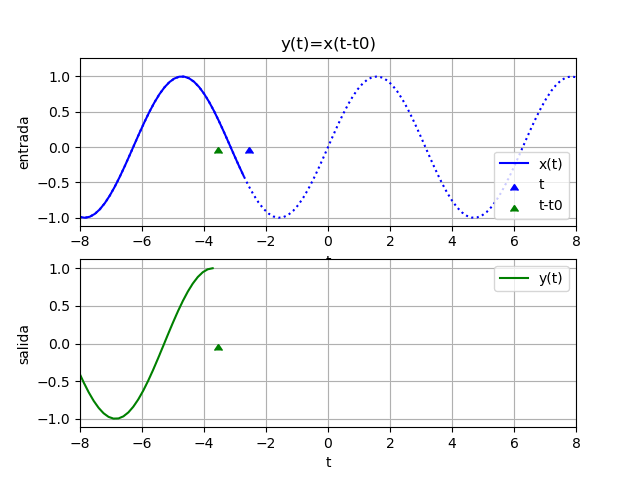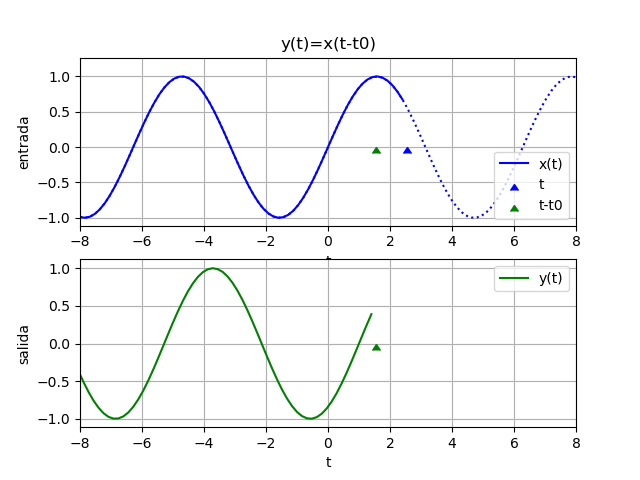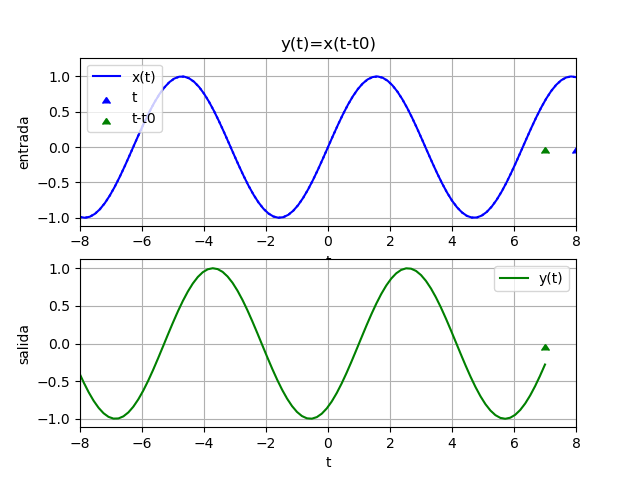
Desde el punto de vista de la fase de la señal, se puede observar que:
\varphi= -\omega_0 t_0 = -2 pi \Big(\frac{t_0}{T_0} \Big)El tema también se trata en el curso de Señales y Sistemas, donde se detalla:
Señales con desplazamiento. escalamiento o inversión en tiempo
3. Ceros de x(t)
Para disponer de una marca referencial de la función, se usará el primer cero de x(t), por simplicidad e obtener mediante:
\cos(\omega t + \varphi) = 0donde se cumple que
\omega t + \varphi = \frac{\pi}{2}que permtite despejar el tiempo cuando ocurre el cero en un periodo:
\omega t = \frac{\pi}{2} - \varphi t_{cero} = \frac{\frac{\pi}{2} -\varphi}{\omega}=\frac{\frac{\pi}{2} - \varphi}{2\pi f_0}[ periodo ] [ desplazamiento ] [ ejercicio ] [ algoritmo ] [ gráfica ] [_telg1034.py _as_dsp ]
..
4. Ejercicio
Referencia: McClellan Fig 2.7 p36
Realizar las gráficas para x(t) con varios valores de f0 = [ 200, 100, 0 ] y observar las diferencias entre ellas.
x(t) =5 \cos(2 \pi f_0 t )Añadir una señal que se desplace en la tercera parte de su periodo (T/3).
Listar los parámetros de cada señal.
[ periodo ] [ desplazamiento ] [ ejercicio ] [ algoritmo ] [ gráfica ] [_telg1034.py _as_dsp ]
..
5. Algoritmo con Sympy
El ejercicio planteado requiere analizar más de una señal, por lo que es conveniente agruparlas en una lista x_senales, para luego usar una funciones como cos_args_one_term() que obtenga los parámetros de cada señal. La función contiene el algoritmo realizado en Señales – Parámetros de sinusoides con Sympy-Python.
Los parámetros se agrupan en un diccionario, identificando cada uno por el nombre en la entrada. Se incorpora en los parámetros el valor de 'periodo'
Por simplicidad, el análisis del argumento del coseno que es una expresión más simple, se realiza en la función auxiliar _cos_arg_freqfase() con instrucciones para simplificar las expresiones cuando se aplican desplazamientos en el tiempo, según se ha mostrado en la parte teórica.
Con los parámetros de cada señal se agrupan las frecuencias, amplitud y fase, añadiendo el primer cero de x(t) como una referencia en el primer periodo y destacar los desplazamientos de una señal. (ejemplo x3(t))
Resultados del algoritmo
señales revisadas: 4 amplitudes: [5, 5, 5, 5] frecuencias: [200, 100, 100, 0] fases: [0, 0, -0.333333333333333*pi, 0] periodo máximo: 0.02 periodo mínimo: 0.005 raíces x_ceros: [0.00125, 0.0025, 0.004166666666667, nan] >>>
Para realizar las gráficas, se unificará el eje de tiempo usando la frecuencia más lenta o periodo máximo. El procedimiento es semejante al ejercicio anterior, añadiendo sub-gráficas (subplots) para cada una de las señales.
Las funciones presentadas se prueban y se mejoran en cada ejercicio o tema de la unidad, por ejemplo aún no se analizan señales con varios término suma. Las funciones se añaden a un archivo telg1034.py para ser reutilizadas y actualizadas.
Instrucciones en Python
# Figura 2.3.1 p35 parámetros en diccionario de x(t) # telg1034 DSP fiec-espol edelros@espol.edu.ec import sympy as sym import numpy as np import matplotlib.pyplot as plt # variables continuas t = sym.Symbol('t', real=True,nonnegative=True) pi = sym.pi DosPi = sym.UnevaluatedExpr(2*sym.pi) # INGRESO x1 = 5*sym.cos(DosPi*(200)*t) x2 = 5*sym.cos(DosPi*(100)*t) x3 = x2.subs(t,t-0.005/3) # adelanto en x(t-t0) x4 = 5*sym.cos(DosPi*(0)*t) x_senales = [x1,x2,x3,x4] x_etiqueta = ['x1(t)','x2(t)','x3(t)','x4(t)'] # PROCEDIMIENTO def cos_args_one_term(x): ''' versión 1. Amplitud, frecuencia en Hz y rad, fase de sin() o cos() referenciado a un término coseno. Entrega diccionario con 'amplitud', 'freq_Hz','freq_rad','fase','periodo'. ''' parametro={} # parámetros en diccionario amplitud = sym.S.One ; T = sym.S.Zero ; fase = sym.S.Zero freq_Hz = sym.S.Zero ; freq_rad = sym.S.Zero x = sym.sympify(x) # expresión a sympy, por si es constante SinSumas = True # Analizar un solo cos o sin if x.is_Add: SinSumas = False if SinSumas: # x(t) un solo cos() o sin(): partes = x.args for unaparte in partes: cond1 = unaparte.has(sym.cos) cond2 = unaparte.has(sym.sin) cond3 = unaparte.has(t) # revisa argumento_cos(w*t+p) if (cond1 or cond2) and cond3: argumento_cos = unaparte.args[0] [freq_Hz,freq_rad,fase] = _cos_arg_freqfase(argumento_cos) if unaparte.has(sym.sin): # convierte a cos(), estandariza fase = fase - sym.pi/2 else: amplitud = amplitud*unaparte # amplitud, revisión numérica if amplitud.is_Number: if amplitud<0: # amplitud con signo positivo amplitud = np.abs(amplitud) fase = fase + sym.pi if isinstance(amplitud,sym.Float): amplitud = float(amplitud) if isinstance(amplitud,sym.Integer): amplitud = int(amplitud) # mantiene forma racional (a/b) de amplitud # periodo T if freq_Hz != sym.S.Zero: T = 1/freq_Hz else: # es una constante T = sym.S.NaN if not(x.has(t)): # es una constante amplitud = x parametro['amplitud'] = amplitud parametro['freq_Hz'] = freq_Hz parametro['freq_rad'] = freq_rad parametro['fase'] = fase parametro['periodo'] = T if SinSumas == False: msg ='x(t) tiene suma de terminos, usar solo un término de la forma:' msg = msg + '\n A*cos(w*t+p) o también A*sin(w*t+p) ... \n' print('cos_sin_args:',x,msg) return(parametro) def _cos_arg_freqfase(argumento_cos): ''' _función_auxiliar_ que obtiene frecuencia (Hz y rad) y fase de la expresion: 2*pi*freq_Hz*t + fase entrega: [freq_Hz,freq_rad,fase] ''' freq_Hz = sym.S.Zero ; freq_rad = sym.S.Zero ; fase = sym.S.Zero argumento_cos = sym.sympify(argumento_cos) # si es constante # simplifica w*t + fase argumento_cos = argumento_cos.doit() # evalua sym.UnevaluatedExpr() argumento_cos = sym.expand(argumento_cos) # simplifica polinomio t argumento_cos = sym.collect(argumento_cos,t) # agrupa terminos t if argumento_cos.is_Add: # términos suma: w*t + fase term_suma = sym.Add.make_args(argumento_cos) for term_k in term_suma: if term_k.has(t): # w*t freq_rad = sym.simplify(term_k/t) freq_Hz = sym.simplify(freq_rad/(2*pi)) else: # fase suma término sin t fase = fase + term_k if argumento_cos.is_Mul: # termino único: w*t if argumento_cos.has(t): freq_rad = sym.simplify(argumento_cos/t) freq_Hz = sym.simplify(freq_rad/(2*pi)) else: fase = fase + argumento_cos parametros_arg = [freq_Hz,freq_rad,fase] return(parametros_arg) # DESARROLLO ----------------------- x_conteo = len(x_senales) # lista frecuencias en señales x_freq = []; x_amplitud =[]; x_fase = []; x_ceros = [] for unasenal in x_senales: parametro = cos_args_one_term(unasenal) freq_k = parametro['freq_Hz'] ampl_k = parametro['amplitud'] fase_k = parametro['fase'] x_freq.append(freq_k) x_amplitud.append(ampl_k) x_fase.append(fase_k) # marca un cero cos(wt+p)=0; wt+p=pi/2 # t_cero = (pi/2-p)/w = (pi/2-p)/(2*pi*f) uncero = sym.nan # si es una constante if abs(freq_k)>0: uncero = (pi/2 - fase_k)/(2*pi*freq_k) uncero = np.around(float(uncero),decimals=15) x_ceros.append(uncero) # periodo máximo y mínimo de señales T_max = 1 ; T_min = 1 freq = np.array(x_freq) freq_min = float(np.min(np.abs(freq))) freq_max = float(np.max(np.abs(freq))) d_freq = np.abs(freq_max - freq_min) # ancho de banda if freq_max>0: T_min = 1/freq_max if d_freq>0: # min y max no son iguales if freq_min>0: T_max = 1/d_freq else: # freq_min==0, selecionar otro T_max freq_min = float(np.min(freq[freq>0])) T_max = 1/freq_min else: # min y max son iguales T_max = 1/freq_min # SALIDA print('señales revisadas: ', x_conteo) print('amplitudes: ', x_amplitud) print('frecuencias:', x_freq) print('fases: ', x_fase) print('periodo máximo:', T_max) print('periodo mínimo:', T_min) print('raíces x_ceros:', x_ceros)
[ periodo ] [ desplazamiento ] [ ejercicio ] [ algoritmo ] [ gráfica ] [_telg1034.py _as_dsp ]
..
6. Gráfica con subplots
Para la parte gráfica se amplían las instrucciones anteriores, añadiendo sub-gráficas (subplots) para cada una de las señales.
Referencia: matplotlib.pyplot.subplots
Para esta ocasión se aborda el desplazamiento considerando que la expresión usada es con Sympy. Para la gráfica que requiere la conversión de forma simbólica a numérica con la instrucción lambdify para más de una señal. como se muestra en el ejercicio.
Conversión de forma simbólica a forma numérica Lambda ( curso: métodos numéricos)
Para la gráfica se pueden usar el parámetro del periodo obtenido en el algoritmo. por lo que será necesario solamente añadir la cantidad de periodos a observar de la señal con menor frecuencia. Para mostrar una curva «suave» se indicará la cantidad de tramos por periodo que se usará para las muestras, se sugiere para el coseno al menos 20.
# GRAFICAR x(t) --------------------------- # INGRESO tramos_T = 20 # tramos por periodo periodos_graf = 4 # periodos en una grafica
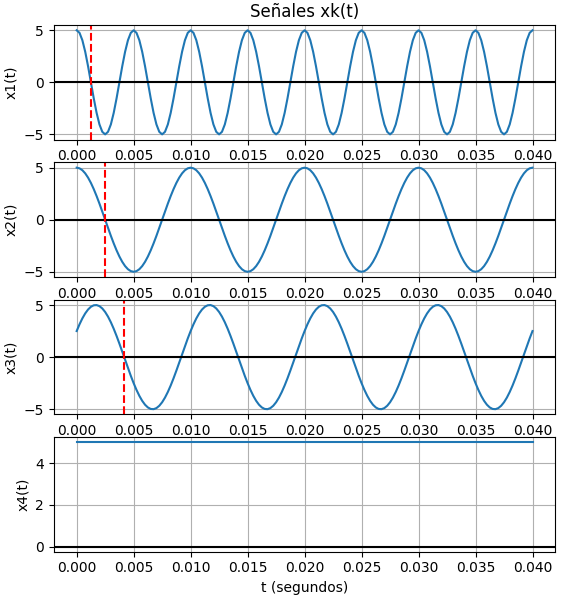 Las señales contenidas en la lista
Las señales contenidas en la lista x_senales requieren muestras de cada una, que se agrupan en xi_k, reutilizando el proceso usando en la gráfica realizada al inicio de la unidad.
El primer cero de la función se marca con una línea vertical discontínua (dashed) de color rojo en los puntos encontrados en x_ceros. Cuando una señal es una constante, el cero se marca con sym.nan (not a number) que no genera la línea roja.
if x_ceros[i]!=sym.nan: graf_x.axvline(x_ceros[i],color='red', linestyle='dashed')
Instrucciones para la gráfica
# GRAFICAR x(t) --------------------------- # INGRESO tramos_T = 20 # tramos por periodo periodos_graf = 4 # periodos en una grafica # PROCEDIMIENTO GRAFICA muestras_T = tramos_T + 1 # intervalo de t entre [a,b] en pasos dt a = 0 b = T_max*periodos_graf dt = T_min/tramos_T # tamaño de paso,tramo, muestreo ti = np.arange(a,b+dt,dt) xi_k = [] # muestras de cada señal x for unasenal in x_senales: # x(t) a forma numérica lambda t: if unasenal.has(t): xk = sym.lambdify(t,unasenal) else: # es constante xk = lambda t: unasenal + 0*t xki = xk(ti) # evalúa en intervalo xi_k.append(np.copy(xki)) # graficar fig_x = plt.figure() for i in range(0,x_conteo,1): graf_sub = x_conteo*100+10+i+1 graf_x = fig_x.add_subplot(graf_sub) graf_x.plot(ti,xi_k[i]) graf_x.set_ylabel(x_etiqueta[i]) graf_x.grid() graf_x.axhline(0,color='black') if i == 0: graf_x.set_title('Señales xk(t)') if x_ceros[i]!=sym.nan: graf_x.axvline(x_ceros[i],color='red', linestyle='dashed') graf_x.set_xlabel('t (segundos)') # graf_x.legend() plt.show()
[ periodo ] [ desplazamiento ] [ ejercicio ] [ algoritmo ] [ gráfica ] [_telg1034.py _as_dsp ]
..
7. Funciones de telg1034.py como dsp
Las funciones para uso en otras unidades se agrupan en el archivo telg1034.py que permite simplificar los algoritmos como el del ejercicio anterior. Las funciones se llaman usando el alias dsp
import telg1034 as dsp
La declaración de variables contínuas como símbolo también se simplifican a una línea. Se incorpora la forma equivalentes de funciones Sympy y Numpy al usar lambdify.
# variables continuas from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes
En los siguientes ejercicios se hará uso de telg1034.py para resumir las funciones de cada algoritmo que se incorpore en la unidad.
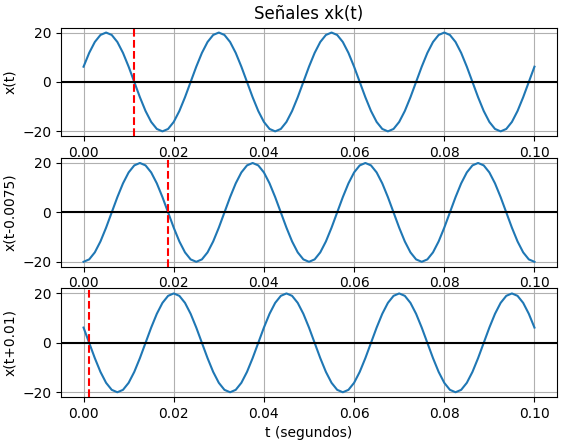
7.1 Ejemplo de desplazamiento por adelanto o retraso
Referencia: McClellan ejercicio 2.4 p39
Usando x(t), realice la gráfica para x(t-t1) cuando t1 = 0.0075. Luego repita el proceso para t1 = -0.01. Revise la dirección del desplazamiento. Para cada caso calcule la fase de la sinusoide desplazada en el tiempo.
x_1(t) = 20 cos(2\pi(40)t - 0.4\pi) x_2(t) = x_1( t-0.0075) x_3(t) = x_1( t-(-0.01))Las señales indicadas en el ejercico se ingresan al algoritmo en la lista x_senales. Los desplazamientos se realizan al sustituir t por (t-desplaza).
# INGRESO
x1 = 20*sym.cos(DosPi*40*t-0.4*pi)
x2 = x1.subs(t,t-0.0075)
x3 = x1.subs(t,t-(-0.01))
con los siguientes resultados:
señales revisadas: 3 amplitudes: [20, 20, 20] frecuencias: [40, 40, 40] fases: [-0.4*pi, -1.0*pi, 0.4*pi] periodo máximo: 0.05 periodo mínimo: 0.025 raices x_ceros: [0.01125, 0.01875, 0.00125] >>>
Para la parte gráfica se usa las instrucciones dadas en la sección [ gráfica ]:
Instrucciones en Python
Instrucciones simplificadas, sin la sección gráfica.
# ejemplo 2.4 p39 x(t) desplazamiento adelanto o retraso # telg1034 DSP fiec-espol edelros@espol.edu.ec import sympy as sym import numpy as np import matplotlib.pyplot as plt import telg1034 as dsp # variables continuas from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x1 = 20*sym.cos(DosPi*40*t-0.4*pi) x2 = x1.subs(t,t-0.0075) x3 = x1.subs(t,t-(-0.01)) x_senales = [x1,x2,x3] x_etiqueta = ['x(t)','x(t-0.0075)','x(t+0.01)'] # PROCEDIMIENTO x_conteo = len(x_senales) # lista frecuencias en señales x_freq = []; x_amplitud =[]; x_fase = []; x_ceros = [] for unasenal in x_senales: parametro = dsp.cos_args_one_term(unasenal) freq_k = parametro['freq_Hz'] ampl_k = parametro['amplitud'] fase_k = parametro['fase'] x_freq.append(freq_k) x_amplitud.append(ampl_k) x_fase.append(fase_k) # marca un cero cos(wt+p)=0; wt+p=pi/2 # t_cero = (pi/2-p)/w = (pi/2-p)/(2*pi*f) uncero = sym.nan # si es una constante if abs(freq_k)>0: uncero = (pi/2 - fase_k)/(2*pi*freq_k) uncero = np.around(float(uncero),decimals=15) x_ceros.append(uncero) # periodo máximo y mínimo de señales T_max = 1 ; T_min = 1 freq = np.array(x_freq) freq_min = float(np.min(np.abs(freq))) freq_max = float(np.max(np.abs(freq))) d_freq = np.abs(freq_max - freq_min) # ancho de banda if freq_max>0: T_min = 1/freq_max if d_freq>0: # min y max no son iguales if freq_min>0: T_max = 1/d_freq else: # freq_min==0, selecionar otro T_max freq_min = float(np.min(freq[freq>0])) T_max = 1/freq_min else: # min y max son iguales T_max = 1/freq_min # SALIDA print('señales revisadas: ', x_conteo) print('amplitudes: ', x_amplitud) print('frecuencias:', x_freq) print('fases: ', x_fase) print('periodo máximo:', T_max) print('periodo mínimo:', T_min) print('raíces x_ceros:', x_ceros)
[ periodo ] [ desplazamiento ] [ ejercicio ] [ algoritmo ] [ gráfica ] [_telg1034.py _as_dsp ]