1. Cinemática - Movimiento en Línea recta con Python
Referencia: Sears-Zemansky Cap2.1 Vol1 Ed.12 p37
Diapositivas. Movimiento en linea recta.
Para plantear el movimiento en línea recta se consideran el punto de partida, llegada y tiempo de recorrido. En Python son variables que pueden obtener diferente valor para cada prueba.
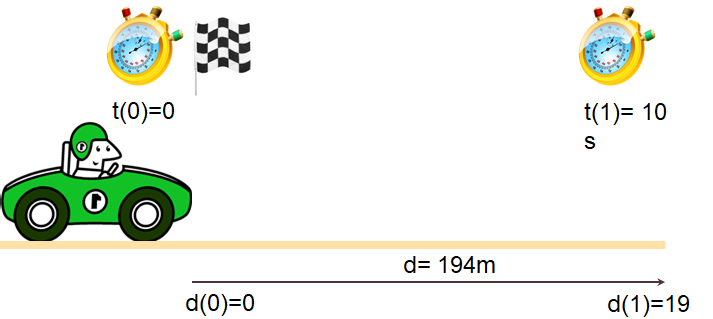
Puede usar Python como calculadora y como programa.
Python como calculadora
Se realizan los cálculos línea por línea
>>> tf=10
>>> d=194
>>> v=d/tf
>>> v
19.4
>>> vkmh=(v/1000)*60*60
>>> vkmh
69.83999999999999
>>> Python como Programa o Algoritmo
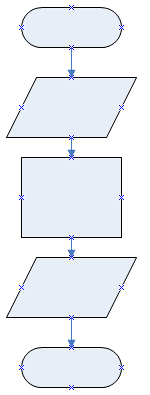
Para que el computador realice los trabajos de cálculo, se deben describir las instrucciones de forma ordenada, simple y muy clara. (Algoritmo)
Una forma de describir un Algoritmo es mediante gráficas conocidas como “Diagramas de Flujo”.
El “Programa” consiste en escribir las instrucciones del algoritmo en un lenguaje para computadora
Generalmente las instrucciones se escriben en inglés, siguiendo un formato (sintaxis) establecido por el lenguaje de programación. Estructuras de Control en programación
Para éste curso, el lenguaje utilizado será Python
En las líneas de inicio, se comienza describiendo la razón por la que escribimos el “algoritmo” escrito en forma de “programa”
# FCNM-ESPOL. Física con python
# cálculo de velocidad
# valores conocidos d y t
En el bloque de INGRESO, se Seleccionan datos conocidos al inicio,se determinan los tipos de datos, sean Variables simples: enteros o reales.
En el algoritmo o programa no se usarán inicialmente las unidades, se supondrá que son predeterminadas
tf = int(input('¿cuantos segundos?: '))
d = float(input('¿distancia recorrida?: '))
En el bloque de procedimiento, para calcular la velocidad en el tramo se escribe la formula, incluso se puede cambiar de mts/seg a Km/h
v = d/tf
vkmh = (v/1000)*60*60
En los bloques de salida y Fin, Se muestran los resultados encontrados y como fin del algoritmo en Python de establece cuando no se encuentran líneas de instrucción
print('Velocidad Media(Km/h)')
print(vkmh)
Algoritmo en Python - Velocidad Media
# FCNM-ESPOL. Física con python
# cálculo de velocidad
# valores conocidos d y t
tf = int(input('¿cuantos segundos?: '))
d = float(input('¿distancia recorrida?: '))
v = d/tf
vkmh = (v/1000)*60*60
print('Velocidad Media(Km/h)')
print(vkmh)
2. Condicionales
Multas por exceso de velocidad con Python
Referencia: Sears-Zemansky Cap2.1 Vol1 Ed.12 p37
Diapositivas Multas por exceso de velocidad.
Situación propuesta: Determinar la velocidad del vehículo en Km/h y poner multas por exceso de velocidad sobre los 50Kmh.
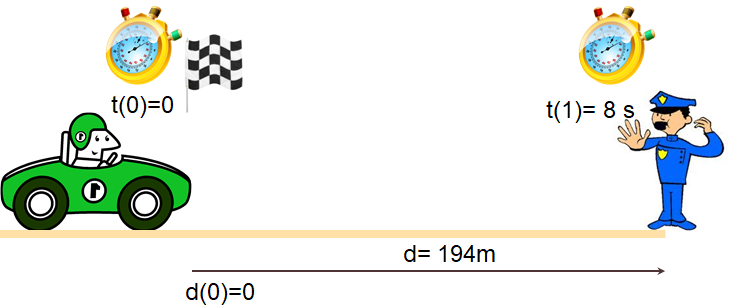
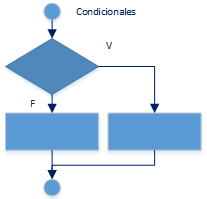
Escrito en Python:
If (condición):
VERDADERO
else:
FALSOLos condicionales, permiten tomar decisiones o elegir las acciones como resultado de una operación lógica,
a>b a=b
a<b a>=b
a<=b ; etc….De la situación propuesta escrita en Python:
if (vkmh>50):
sancion=1
else:
sancion=0
Con lo que el algoritmo de velocidad media se convierte en:
Algoritmo en Python - Multa por velocidad limite
# FCNM-ESPOL. Física con python
# cálculo de multa por velocidad límite
# valores conocidos d y t
# sancion si exede los 50km/h
tf=int(input('¿cuantos segundos?: '))
d=float(input('¿distancia recorrida?: '))
v=d/tf
vkmh=(v/1000)*60*60
if (vkmh>50):
sancion=1
else:
sancion=0
print('Velocidad Media(Km/h)')
print(vkmh)
if (sancion==1):
print('Tiene sancion por exceso de velocidad sobre 50 Km/h')
Ejercicio propuesto
Ampliar el uso del tema propuesto, solicitando la variable de velocidad “limite” para decidir si aplica una sanción
- Zona escolar: 20 Km/h
- Zona urbana: 50 Km/h
- Vía rápida urbana: 60 Km/h
- Carretera: 90 Km/h
Algoritmo en Python - Velocidad Media
# FCNM-ESPOL. Física con python
# cálculo de velocidad
# valores conocidos d y t
tf = int(input('¿cuantos segundos?: '))
d = float(input('¿distancia recorrida?: '))
v = d/tf
vkmh = (v/1000)*60*60
print('Velocidad Media(Km/h)')
print(vkmh)
3. Tablas - Lazos/bucles y arreglos 1D
Velocidad por tramos con Python
Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
Diapositivas: Con varios puntos observados.
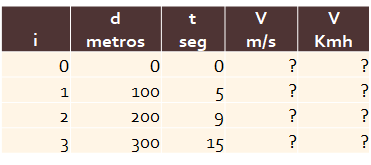
Tomar lecturas de distancias y tiempos recorridos, para obtener velocidades por tramo en Kmh
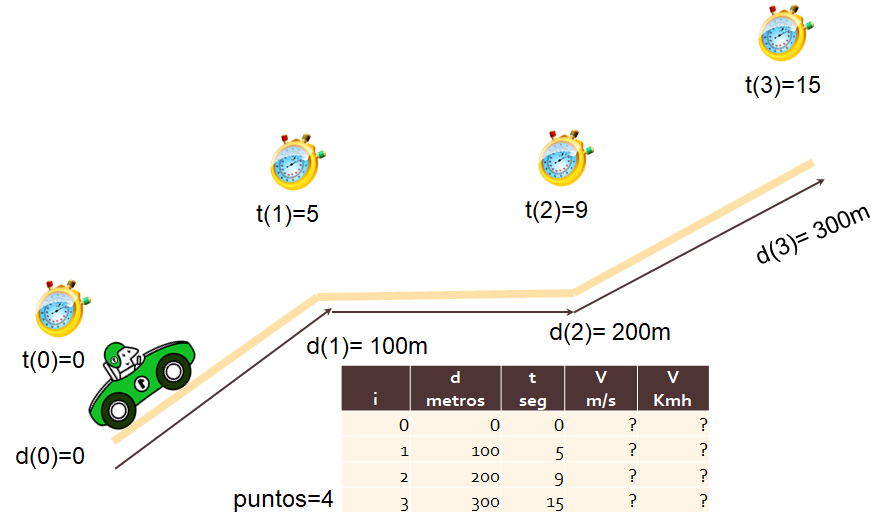
Lazos para Repetir
Usados cuando hay que repetir una operación o bloque de procedimiento. Se expresa como:
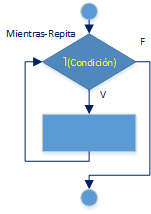
Mientras (condición):
repita
while (condición):
…Lazos/Bucles – Estructuras para Repetir o iterar
Arreglos Vectores – de una dimensión
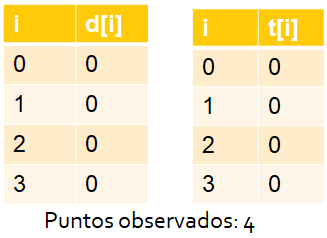
Usados cuando hay que almacenar una lista de datos, similar a la del problema propuesto.
Se requiere importar la librería Numpy para facilitar el manejo de los datos. np es el alias de la librería
import numpy as npSe inicializa el arreglo, llenándolo con ceros
d=np.zeros(puntos,dtype=float)
t=np.zeros(puntos,dtype=int)
i=0
Los arreglos inician en la fila 0, conocida como punto inicial.
Es necesario indicar los datos son enteros(int) o reales (float).
Vectores – Arreglos de una dimensión
resultado del algoritmo:
>>>
¿puntos observados?:4
distancia recorrida (m):0
tiempo transcurrido (s):0
distancia recorrida (m):100
tiempo transcurrido (s):5
distancia recorrida (m):200
tiempo transcurrido (s):9
distancia recorrida (m):300
tiempo transcurrido (s):15
Velocidades en Kmh:
0.0
72.0
90.0
60.0Algoritmo: Velocidad por tramos recorridos
# FCNM-ESPOL. Física con python
# varios tramos de recorrido
import numpy as np
puntos=int(input('¿puntos observados?:'))
d=np.zeros(puntos,dtype=float)
t=np.zeros(puntos,dtype=int)
i=0
while (i<puntos):
d[i]=float(input('distancia recorrida (m):'))
t[i]=int(input('tiempo transcurrido (s):'))
i=i+1
#Procedimiento
v=np.zeros(puntos,dtype=float)
vkmh=np.zeros(puntos,dtype=float)
v[0]=0
vkmh[0]=0
i=1
while (i<puntos):
v[i]=(d[i]-d[i-1])/(t[i]-t[i-1])
vkmh[i]=(v[i]/1000)*60*60
i=i+1
#Salida
print('Velocidades en Kmh:')
i=0
while (i<puntos):
print(vkmh[i])
i=i+1
4. Ejercicio para Taller
Velocidades por tramos, Implementar el algoritmo en Python.
| Lectura | d | t | V | V |
| metros | seg | m/s | Kmh | |
| 0 | 0 | 0 | ||
| 1 | 100 | 5 | ||
| 2 | 200 | 9 | ||
| 3 | 300 | 15 | ||
| 4 | 400 | 19 | ||
| 5 | 500 | 25 | ||
| 6 | 600 | 33 | ||
| 7 | 700 | 38 | ||
| 8 | 700 | 45 | ||
| 9 | 800 | 55 | ||
| 10 | 800 | 15 |
5. Contadores, Acumuladores y arreglos
Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
Diapositivas: identificando cada punto observado.
Identificar cada lectura de datos para el ejercicio de velocidad por tramos requiere un índice o número que sea único para cada lectura.
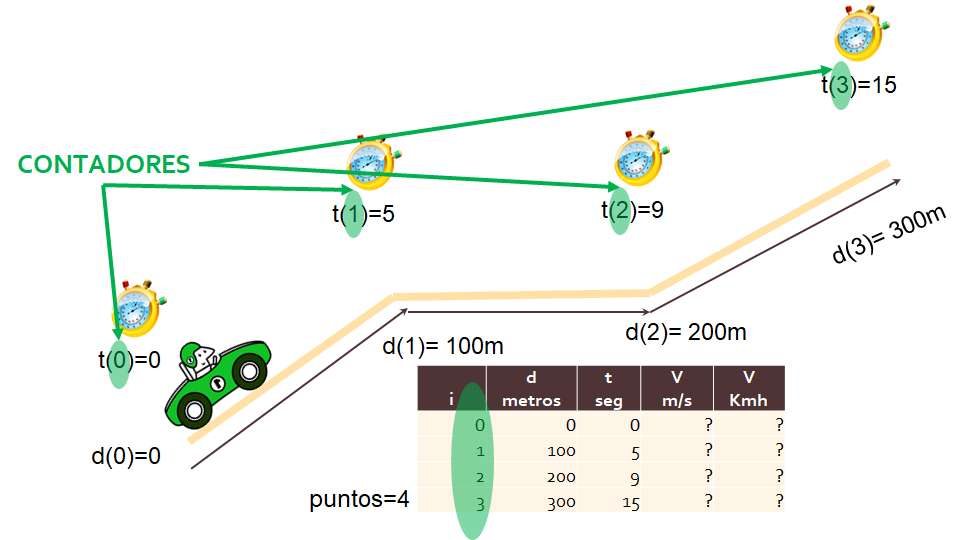
Se usa el concepto de contadores y acumuladores para llevar el control de los índices:
Contadores y Acumuladores en programación
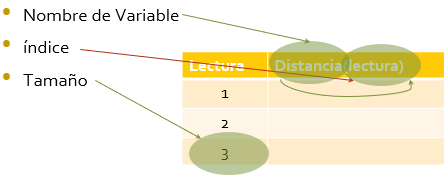
Los arreglos permiten almacenar listas de datos, tal como las usadas en el ejemplo anterior:
>>d(1)
Ans = 100
>> t(3)
Ans=15se observa que todas las variables tipo arreglo tienen:
Taller: Velocidad media
En el ejercicio mostrado, calcular la velocidad media como el promedio de los valores de velocidades.
6. Gráficas tiempo vs distancia con Python
Referencia: Sears-Zemansky Cap2.2 Vol1 Ed.12 p39
Diapositivas: Graficando tiempo vs distancia, velocidad y aceleración.
Situación propuesta: Observar en una gráfica los datos del ejercicio anterior.
Tomar lecturas de distancias y tiempos recorridos, para obtener velocidades por tramo en Kmh
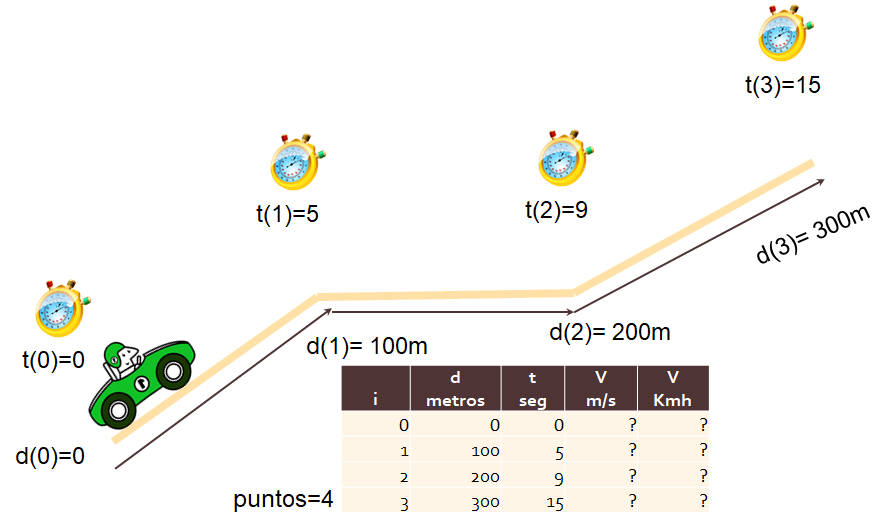
Usaremos los resultados del ejercicio: velocidadtramos.py
Ejecutar el archivo con los datos del problema mostrado para obtener en memoria los resultados siguientes mostrados.
>>> d
array([ 0., 100., 200., 300.])
>>> t
array([ 0, 5, 9, 15])
>>> v
array([ 0. , 20. , 25. , 16.66666667])
>>> vkmh
array([ 0., 72., 90., 60.])
>>>Gráfica desde linea de instrucciones
Se puede crear la gráfica paso a paso desde el Shell de
Python
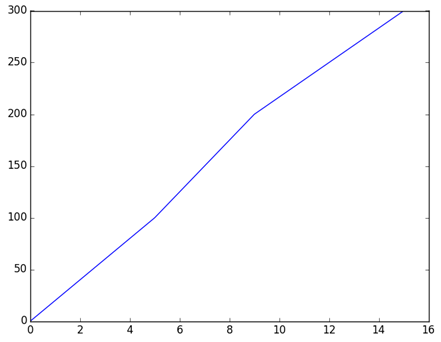
Se requiere importar la librería para gráficas con el álias “plt” que es estandarizado.
>>> import matplotlib.pyplot as pltSe crea la línea a graficar
>>> plt.plot(t,d)Mostrar el gráfico construido
>> plt.show()Añadir títulos de gráfico
>>> import matplotlib.pyplot as pltUsar la forma interactiva para generar el gráfico, No se usa en el script
>>> plt.ion()
>>> plt.plot(t,d)
[<matplotlib.lines.Line2D object at 0x05A605F0>]
>>> plt.title('Distancia recorrida vs tiempo acumulado')
<matplotlib.text.Text object at 0x05A50630>
>>> plt.xlabel('tiempo segundos')
<matplotlib.text.Text object at 0x05A0A910>
>>> plt.ylabel('distancia en metros')
<matplotlib.text.Text object at 0x05A3C430>Desconetar la interactiva con plt.ioff() y en el script:
>>> plt.show()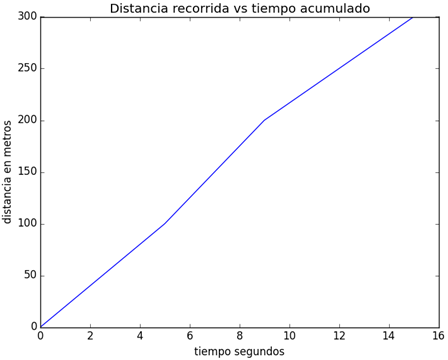
Colores y marcas de punto
Nos permiten realizar las gráficas de datos disponibles en un arreglo.
Se utiliza: plt.plot ( x, y, propiedades);
Las propiedades como el color y el punto se especifican entre apóstrofes:
| Letra | Color | Símbolo | forma | |
| b | Blue (azul) | . | Punto | |
| g | Green(verde) | o | círculo | |
| r | Red (rojo) | x | Marca de X | |
| y | Yellow (amarillo) | + | Marca de + | |
| k | Black (negro) | s | cuadro | |
| w | White(blanco | v | Triángulo | |
| m | magenta | o | pentagrama |
las instrucciones a usar son:
>>> plt.plot(t,v,'ro-')
[]
>>> plt.title('velocidad observada vs tiempo acumulado')
>>> plt.xlabel('tiempo en segundos')
>>> plt.ylabel('velocidad en m/s')
>>> plt.show()con lo que se obtiene
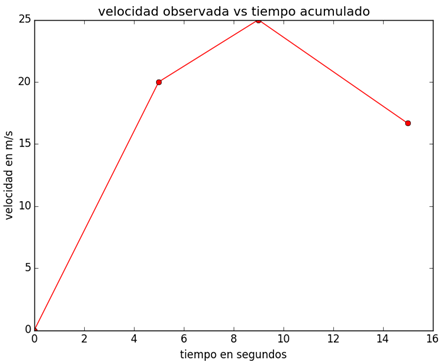
Taller - Aceleración media
Referencia: Física Universitaria Sears –Zemanski. Vol 1. Edición 12. Ejercicio 2.12
(2.12). Un piloto de pruebas de Automotores Galaxia, S.A., está probando un nuevo modelo de automóvil con un velocímetro calibrado para indicar m/s en lugar de mi/h. Se obtuvo la siguiente serie de lecturas durante una prueba efectuada en una carretera recta y larga:
| tiempo(s) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| Rapidez(m/s) | 0 | 0 | 2 | 6 | 10 | 16 | 19 | 22 | 22 |
a) Calcule la aceleración media en cada intervalo de 2 s.
¿La aceleración es constante? ¿Es constante durante alguna parte de la prueba?
b) Elabore una gráfica vx - t con los datos, usando escalas de 1 cm = 1 s horizontalmente, y 1 cm = 2 m/s verticalmente.
Dibuje una curva suave que pase por los puntos graficados.
Mida la pendiente de la curva para obtener la aceleración instantánea en: t =9 s, 13 s y 15 s.
Desarrollar el literal a) en Python
tiempo = [0.0, 2, 4, 6, 8, 10, 12, 14, 16]
rapidez = [0, 0, 2, 6, 10, 16, 19, 22, 22]Subgráficos (subplots)
Permiten realizar grupos de gráficos en un esquema tipo matricial.
gráfica, cuadro=plt.subplots(2)
El índice del primer cuadro es el cero
cuadro[0].plot(x,y)
El siguiente cuadro es el uno
cuadro[1].step(tiempo,acelera,'r')
Se pueden añadir o cambiar las propiedades de un cuadro:
cuadro[0].set_title('tiempo vs rapidez')
Las instrucciones en Python desde la toma de datos son
# FCNM-ESPOL. Física con python
# calcular aceleracion media por intervalo
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
puntos = int(input('¿puntos observados?:'))
tiempo = np.zeros(puntos,dtype=int)
rapidez = np.zeros(puntos,dtype=float)
i = 0
while (i<puntos):
tiempo[i] = int(input('tiempo transcurrido (s):'))
rapidez[i] = float(input('distancia recorrida (m/s):'))
i = i + 1
# PROCEDIMIENTO
acelera = np.zeros(puntos,dtype=float)
i = 0
acelera[0] = 0
i = 1
while (i<puntos):
acelera[i] = rapidez[i]-rapidez[i-1]
i = i + 1
En el bloque de salida se puede añadir:
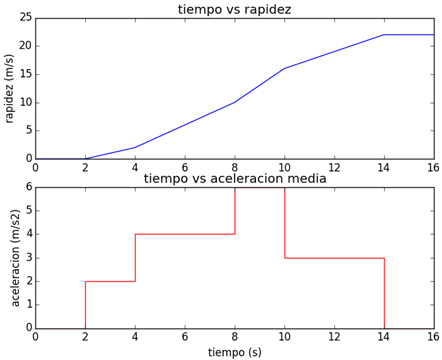
#grafica con dos cuadros
grafica,cuadro = plt.subplots(2)
cuadro[0].plot(tiempo,rapidez)
cuadro[0].set_title('tiempo vs rapidez')
cuadro[0].set_ylabel('rapidez (m/s)')
cuadro[1].step(tiempo,acelera,'r')
cuadro[1].set_title('tiempo vs aceleracion media')
cuadro[1].set_xlabel('tiempo (s)')
cuadro[1].set_ylabel('aceleracion (m/s2)')
plt.show()