1. Euler a coseno
Como resultado del producto de sinusoides usando la fórmula de Euler se obtienen términos exponenciales para las partes de frecuencia y fase.
El proceso inverso requiere reagrupar las expresiones de la lista Xe_senales por cada término suma.
unaSenal = sym.powsimp(unaSenal,combine='exp')Luego simplificar sus exponentes tomando como factor común el número complejo I. En éste último paso es necesario tomar en cuenta el signo del término que contiene t.
factor_I = I
if t1<sym.S.Zero:
factor_I = -I
exponente = factor_I*(sym.expand(exponente/factor_I))Este proceso se debe aplicar a cada término suma de la expresión, requiriendo un análisis detallado de cada término como se muestra en el algoritmo.
Al terminar de reordenar la expresión se convierte nuevamente a la forma coseno usando la instrucción:
Xe_to_cos = Xe_sum.rewrite(sym.cos)El proceso de inverso se agrupa en la función euler_to_cos_list(Xe_senales).
La mejor forma de escribir el algoritmo paso a paso es usando un ejemplo, con el que si usa el algoritmo básico desarrollado en Producto de sinusoides , podrá observar que el resultado debe considerar mas casos de los presentados.
2. Ejercicio
Referencia: McClellan ejemplo 3.3 p77
La señal x(t) es el producto de dos señales de frecuencias 9 y 200 Hz según la expresión mostrada, realice el espectro de frecuencias correspondiente. muestre la expresión de cosenos más simples usando las fórmulas de Euler.
x(t) = 2 \cos (2 \pi 9 t) \cos( 2 \pi*200*t)2. Desarrollo analítico
Se usa la fórmula de Euler para cada parte de la expresión:
2 \cos (2 \pi (9) t) = e^{j 2\pi (9) t} +e^{-j 2\pi (9)t} \cos( 2 \pi (200) t) = \frac{1}{2} e^{j 2\pi (200) t} +\frac{1}{2}e^{-j 2\pi (200)t} x(t) = 2 \cos (2 \pi 9 t) \cos( 2 \pi*200*t) x(t) = \Big(e^{j 2\pi (9) t} +e^{-j 2\pi (9)t} \Big) \Big( \frac{1}{2} e^{j 2\pi (200) t} + \frac{1}{2}e^{-j 2\pi (200)t} \Big) = \frac{1}{2} e^{j 2\pi (9) t} e^{j 2\pi (200) t} + \frac{1}{2} e^{j 2\pi (9) t}e^{-j 2\pi (200)t} +\frac{1}{2} e^{-j 2\pi (9)t} e^{j 2\pi (200) t} + \frac{1}{2}e^{-j 2\pi (9)t} e^{-j 2\pi (200)t} = \frac{1}{2}e^{j 2\pi (200) t + j 2\pi (9) t} + \frac{1}{2} e^{-j 2\pi (200) t + j 2\pi (9) t} +\frac{1}{2} e^{j 2\pi (200) t -j 2\pi (9)t} + \frac{1}{2}e^{-j 2\pi (200)t -j 2\pi (9)t} = \frac{1}{2}e^{j 2\pi (209) t } + \frac{1}{2} e^{-j 2\pi (191) t} +\frac{1}{2} e^{j 2\pi (191) t} + \frac{1}{2} e^{-j 2\pi (209)t} x(t) = \cos (2\pi(191)t) + \cos (2 \pi (209)t)El resultado obtenido usando la función euler_to_cos_list() es:
x(t): 2*cos(9*t*(2*pi))*cos(200*t*(2*pi))
x_senales:
senal: 2*cos(9*t*(2*pi))*cos(200*t*(2*pi))
euler: exp(-209*I*t*2*pi)/2 + exp(-191*I*t*2*pi)/2 + exp(191*I*t*(2*pi))/2 + exp(209*I*t*(2*pi))/2
x_expand:
cos(382*pi*t) + cos(418*pi*t)
x_espectro:
freq : [-209. -191. 191. 209.]
ampl : [1/2 1/2 1/2 1/2]
fase : [0 0 0 0]
etiq : ['1/2' '1/2' '1/2' '1/2']La gráfica de espectro muestra las señales desplazadas en frecuencia resultado del producto de senoidales.
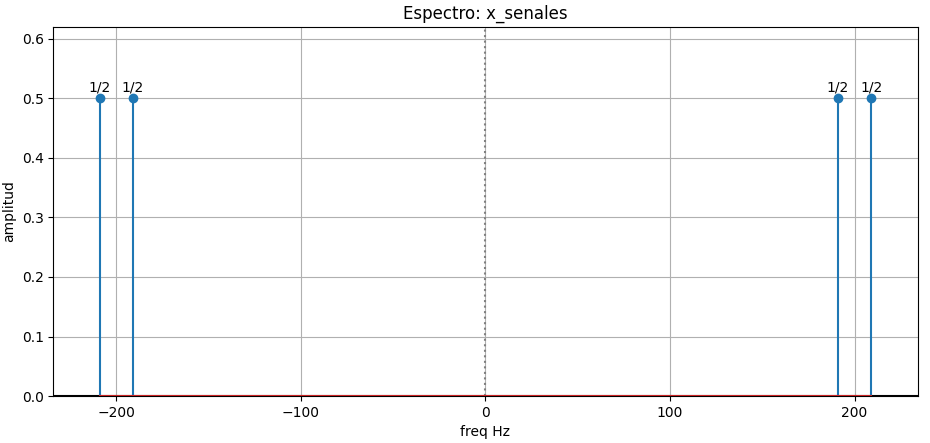
Se adjunta la gráfica de tiempo como complemento

3. Algoritmo con Python
El algoritmo en Python incluye la función euler_to_cos_list(Xe_senales) que se añade a telg1034.py para el uso en los otros ejercicios cuando se busca simplificar las expresiones de x_senales.
# ejemplo 3.3 p77 Disminuir la diferencia entre frecuencias
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import telg1034 as dsp
# variables
from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes
# INGRESO
x1 = 2*sym.cos(DosPi*9*t)
x2 = sym.cos(DosPi*200*t)
x = x1*x2
# PROCEDIMIENTO
x_senales = dsp.x_list_term_Add(x)
x_conteo = len(x_senales)
Xe_senales = dsp.cos_to_euler_one_term(x_senales)
Xe_espectro = dsp.cos_spectrum_list(x_senales)
def euler_to_cos_list(Xe_senales):
'''Xe_senales a coseno, simplifica x(t) en formato Euler
'''
Xe_conteo = len(Xe_senales)
x_expand = sym.S.Zero
for i in range(Xe_conteo):
unaSenal = Xe_senales[i]
if unaSenal.has(sym.UnevaluatedExpr):
unaSenal = unaSenal.doit()
unaSenal = sym.powsimp(unaSenal,combine='exp')
if unaSenal.is_Add:
term_sum = unaSenal.args
Xe_sum = sym.S.Zero
for unterm in term_sum:
factor_mul = unterm.args
if len(factor_mul)>0: # unterm no es constante
Xe_term = sym.S.One
for unfactor in factor_mul:
if unfactor.has(t) and unfactor.has(sym.exp):
exponente = unfactor.args[0]
expresion = sym.expand(exponente/I)
constante = expresion.subs(t,0)
expresion = expresion - constante
t1 = expresion.subs(t,1)
factor_I = I
if t1<sym.S.Zero:
factor_I = -I
exponente = factor_I*(sym.expand(exponente/factor_I))
el_factor = sym.exp(exponente)
else: # el factor es constante
el_factor = unfactor
Xe_term = Xe_term*el_factor
else: # unterm es constante
Xe_term = unterm
Xe_sum = Xe_sum + Xe_term
Xe_to_cos = Xe_sum.rewrite(sym.cos)
else:
Xe_to_cos = unaSenal
x_expand = x_expand + Xe_to_cos
return(x_expand)
x_expand = euler_to_cos_list(Xe_senales)
# SALIDA
print('x(t):',x)
print('x_senales: ')
for i in range(x_conteo):
print('senal: ',x_senales[i])
print(' euler:',Xe_senales[i])
print('x_expand: ')
print(' ',x_expand)
print('x_espectro:')
for unparam in Xe_espectro:
print(unparam,':',Xe_espectro[unparam])
4. Gráficas de espectro de frecuencias y señal en tiempo
La parte gráfica es la usada en la sección de Producto de señales
# GRAFICAS de espectro de frecuencias ---------
freq = Xe_espectro['freq']
magnitud = Xe_espectro['ampl']
etiqueta = Xe_espectro['etiq']
mag_max = float(max(magnitud))
freq_max = float(max(freq))
# grafica
graf_dx = 0.12
fig_espectro = plt.figure()
graf_fasor = fig_espectro.add_subplot()
# grafica magnitud
graf_fasor.set_xlim([-freq_max*(1+graf_dx),freq_max*(1+graf_dx)])
graf_fasor.set_ylim([0,mag_max*(1+graf_dx*2)])
graf_fasor.axhline(0,color='black')
graf_fasor.axvline(0,linestyle='dotted',color='grey')
graf_fasor.stem(freq,magnitud)
# etiquetas de fasor
for k in range(0,len(freq),1):
texto = etiqueta[k]
x_text = freq[k]
y_text = magnitud[k]
plt.annotate(texto,xy=(x_text,y_text), xytext=(0,5),
textcoords='offset points',ha='center')
graf_fasor.grid()
graf_fasor.set_xlabel('freq Hz')
graf_fasor.set_ylabel('amplitud')
graf_fasor.set_title('Espectro: x_senales')
#plt.show()
# GRAFICAR x(t) ---------------------------
# INGRESO
x_senales_graf = [x1,x2,x] # para graficar
x_etiqueta = ['x1(t)','x2(t)','x1(t)x2(t)']
x_tipolinea = ['dashed','dotted','solid']
tramos_T = 20 # tramos por periodo
periodos_graf = 2 # periodos en una grafica
# PROCEDIMIENTO GRAFICA
x_conteo_graf = len(x_senales_graf)
# etiquetas si están vacias
if len(x_etiqueta)==0:
if x_conteo_graf > 1:
for i in range(0,x_conteo_graf-1,1):
x_etiqueta.append('x'+str(i)+'(t)')
x_tipolinea.append('dotted')
x_etiqueta.append('x(t)')
x_tipolinea.append('solid')
[T_min,T_max] = dsp.periodo_minmax(freq)
x_conteo = len(x_senales_graf)
muestras_T = tramos_T + 1
# intervalo de t entre [a,b] en pasos dt
a = 0
b = T_max*periodos_graf
dt = T_min/tramos_T # tamaño de paso,tramo, muestreo
ti = np.arange(a,b+dt,dt)
xi_k = [] # muestras de cada señal x
for unasenal in x_senales_graf:
# x(t) a forma numérica lambda t:
if unasenal.has(t):
xk = sym.lambdify(t,unasenal)
else: # es constante
xk = lambda t: unasenal + 0*t
xki = xk(ti) # evalúa en intervalo
xi_k.append(np.copy(xki))
# graficar
fig_x = plt.figure()
graf_x = fig_x.add_subplot()
for i in range(0,x_conteo_graf,1):
color_i = dsp._graf_lineacolor_i(i)
graf_x.plot(ti,xi_k[i], color=color_i,
linestyle=x_tipolinea[i],
label=x_etiqueta[i])
graf_x.axhline(0,color='black')
graf_x.set_title('Señales xk(t)')
graf_x.set_xlabel('t (segundos)')
graf_x.set_ylabel('x_senales')
graf_x.grid()
graf_x.legend()
plt.show()
5. Tarea
Referencia: McClellan ejercicio 3.1 p75
Verificar el algoritmo con
x(t) = \sin ^2 (10 \pi t)que debe dar resultado:
x(t): sin(10*pi*t)**2
x_senales:
senal: sin(10*pi*t)**2
euler: -exp(20*I*pi*t)/4 + 1/2 - exp(-20*I*pi*t)/4
x_expand:
1/2 - cos(20*pi*t)/2
freq_min: 10.0
freq_centro: 10.0
freq_max: 10.0
ancho de banda BW: 0.0
x_espectro:
freq : [-10. 0. 10.]
ampl : [1/4 1/2 1/4]
fase : [pi 0 pi]
etiq : ['1/4$ e^j(\\pi)$' '1/2' '1/4$ e^j(\\pi)$']