1. Espectro de frecuencias de x[n]
Referencia: McClellan 4.1.4 p129
De forma semejante al Espectro para Operaciones en dominio de tiempo y frecuencia, se aplica el concepto de frecuencias en radiantes. El espectro permitirá analizar las señales alias: alias principal junto a otros alias generados con ±2π en cada frecuencia. Por ejemplo, para:
x1[n] = cos(0.4π n)
Es señal básica con frecuencia en radianes en 0.4π, sería alias principal, con componentes en ±0.4π. En el dominio discreto 'n', las señales alias se forman con cada componente desplazados en 2πk a la derecha y -2πk a la izquierda. Siendo k un número entero. Para k=1.
| Señal | otros alias, k=1 |
| alias principal ω1[n] = 0.4π | ω3[n] = 0.4π + 2π = 2.4 ω4[n] = 0.4π - 2π = -1.6 |
| alias folded (pliegue negativo) ω2[n] = - 0.4π | ω5[n] = -0.4π + 2π = 1.6 ω6[n] = -0.4π - 2π = -2.4 |
el espectro con señales alias para k=1 es:
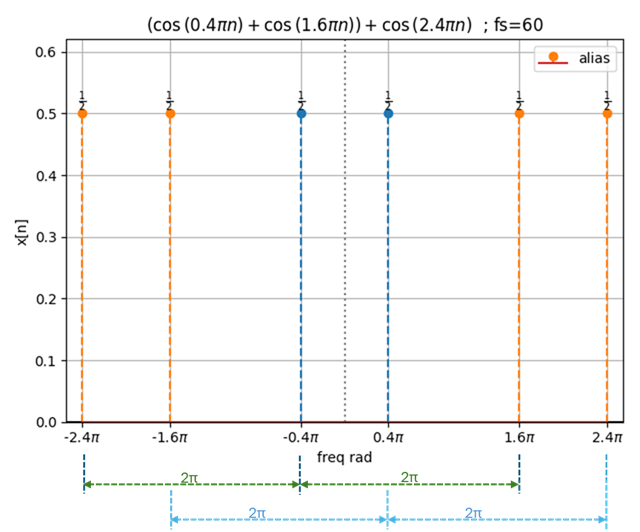
2. Algoritmo en Python
El punto de partida es el algoritmo usado en Espectro para Operaciones en dominio de tiempo y frecuencia, donde las operaciones son semejantes y aplicadas al dominio 't', que deben cambiarse al domino 'n'. Se aplica un cambio de variable y una bandera 'esdiscreta' para ajustar el eje de frecuencias a radianes en el análisis de la función cos_spectrum_list(x_senales) del archivo telg1034.py. con lo que se logra obtener básicamente los resultados del espectro ajustados al nuevo dominio
#...
for i in range(0,x_conteo,1):
unasenal = x_senales[i]
# revisa si unasenal es discreta con n
esdiscreta = False
varindepend = unasenal.free_symbols
if (n in varindepend) and not(t in varindepend):
unasenal = unasenal.subs(n,t)
esdiscreta = True
# analiza unasenal con t
#...cuando la señal es discreta, las frecuencias consideran el factor 2π, que se separaba cuando se calculaban en Hz.
if esdiscreta:
freq_k = freq_k*2*pi
x_freq_spectr.append(freq_k)con lo que el algoritmo se ajusta a la variable y es funcional.
Para la sección gráfica, se puede considerar el factor π como un elemento a simplificar en el vector de frecuencias. Se revisa si existe el factor en el arreglo de frecuencias y se procede a separarlo dentro del algoritmo de espectro para t. Se actualizan los valores en los resultados.
...
# revisa factor pi en freq_n
unfactor = sym.S.One ; factor_pi = False
freqn_conteo = len(freq_n)
for i in range(0,freqn_conteo,1):
if freq_n[i].has(pi):
factor_pi = True
if factor_pi:
freq_n = np.array(freq_n/pi,dtype=float)
unfactor = pi
# actualiza espectro de señal con factor pi
un_espectro_n['freq_factor'] = unfactor
un_espectro_n['freq'] = freq_n
...2.1 Revisión de señales "alias" en x_senales en algoritmo para espectro
Para tener un marcador de frecuencias alias en las señales analizadas, se compara cada frecuencia del espectro para diferentes valores de k en la operación ±2π, mientras no sobrepase la frecuencia máxima del intervalo de freq.
...
# aliasing, Revisa espectro de frecuencias
freq_conteo = len(freq_n)
freq_alias = np.zeros(freq_conteo,dtype=bool)
for i in range (0,freq_conteo,1):
unafreq = freq_n[i]
k = 1
unalias = unafreq + k*2
while unalias<=freq_max:
for j in range(i+1,freq_conteo,1):
if abs(unalias - freq_n[j])<tolera:
if abs(freq_n[i])>abs(freq_n[j]):
freq_alias[i] = True
else:
freq_alias[j] = True
k = k+1
unalias = unafreq + k*2
un_espectro_n['freq_alias'] = freq_alias
...Se marcan las frecuencias alias en la lista freq_alias para diferenciarlas con otro color en la gráfica de espectro, obteniendo el resultado presentado en el ejercicio.
2.2 Algoritmo en Python
La señal para el espectro se construye con los componentes alias presentados en la parte teórica. Se analiza solo la señal x4[n] para el espectro.
El parámetro tolera en el bloque de ingreso es la tolerancia para redondear los valores de frecuencia en la gráfica cuando tienen varios dígitos decimales.
# ejercicio 4.4 p130 Espectro de señales senoidales discretas
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import telg1034 as dsp
# variables continuas
from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes
# variables discretas
from telg1034 import n
# INGRESO
with sym.evaluate(False): # no simplificar freq angular w >2*pi
x1 = sym.cos(0.4*pi*n)
x2 = sym.cos(1.6*pi*n)
x3 = sym.cos(2.4*pi*n)
xn = x1+x2+x3
x_etiqueta_n = 'x[n]'
fs = 60 # muestreo discreto, freq_sampling
fs_veces = 12 # suavizar x(t), sobremuestreo
muestrasN = 6 + 1 # para x[n]
tolera = 1e-9 # tolerancia a error, números iguales
# PROCEDIMIENTO
titulo = xn # copia para titulo de grafico (antes de procesar)
# espectro x[n]
# Ref: Blog|Espectro-Operaciones en dominio de tiempo y frecuencia
xn = xn.subs(pi,np.pi) # mantener valores >2pi
x_term = dsp.x_list_term_Add(xn)
Xe_term = dsp.cos_to_euler_one_term(x_term)
x_term_expand = dsp.euler_to_cos_list(Xe_term)
un_espectro_n = dsp.cos_spectrum_list(x_term)
un_espectro_n['x_expand'] = x_term_expand
# espectro de cada señal
freq_n = un_espectro_n['freq']
ampl_n = un_espectro_n['ampl']
fase_n = un_espectro_n['fase']
etiq_n = np.array(un_espectro_n['etiq'])
# revisa factor pi en freq_n
unfactor = sym.S.One ; factor_pi = False
freqn_conteo = len(freq_n)
for i in range(0,freqn_conteo,1):
if freq_n[i].has(pi):
factor_pi = True
if factor_pi:
freq_n = np.array(freq_n/pi,dtype=float)
unfactor = pi
# actualiza espectro de señal con factor pi
un_espectro_n['freq_factor'] = unfactor
un_espectro_n['freq'] = freq_n
# ancho de banda, freq_max y freq_min
freq_posi = freq_n[freq_n>0]
freq_max = float(max(freq_posi))
freq_min = 0
if len(freq_posi)>0:
freq_min = float(min(freq_posi))
freq_centro = (freq_max+freq_min)/2
un_espectro_n['freq_max'] = freq_max
un_espectro_n['freq_min'] = freq_min
un_espectro_n['BW'] = freq_max-freq_min
# aliasing, Revisa espectro de frecuencias
freq_conteo = len(freq_n)
freq_alias = np.zeros(freq_conteo,dtype=bool)
for i in range (0,freq_conteo,1):
unafreq = freq_n[i]
k = 1
unalias = unafreq + k*2
while unalias<=freq_max:
for j in range(i+1,freq_conteo,1):
if abs(unalias - freq_n[j])<tolera:
if abs(freq_n[i])>abs(freq_n[j]):
freq_alias[i] = True
else:
freq_alias[j] = True
k = k+1
unalias = unafreq + k*2
un_espectro_n['freq_alias'] = freq_alias
# SALIDA
print('senal[n]: ',titulo)
print('senal[n]: ',xn)
print(' espectro:')
for parametro in un_espectro_n:
print(' ',parametro,':',un_espectro_n[parametro])
3. Gráfica espectro dominio n
Se añaden la gráfica para el espectro de frecuencias ajustada al dominio n
# GRAFICAS de espectro de frecuencias discretas---------
graf_dx = 0.12
fig_espectro = plt.figure()
freq_alias_conteo = np.sum(freq_alias)
ampl_max = float(max(ampl_n))*(1+graf_dx*2)
freq_max = float(max(un_espectro_n['freq_max'],1))*(1+graf_dx/2)
# grafica entorno
graf_fasorn = fig_espectro.add_subplot(111)
graf_fasorn.set_xlim([-freq_max,freq_max])
graf_fasorn.set_ylim([min([min(ampl_n),0]),ampl_max])
graf_fasorn.grid()
graf_fasorn.axhline(0,color='black')
graf_fasorn.axvline(0,linestyle='dotted',color='grey')
texto = '$' + sym.latex(titulo)+'$' +' ; fs='+str(fs)
graf_fasorn.set_title(texto)
graf_fasorn.set_ylabel(x_etiqueta_n)
graf_fasorn.set_xlabel('freq rad')
# grafica magnitud
freq_noalias = np.invert(freq_alias)
graf_fasorn.stem(freq_n[freq_noalias],ampl_n[freq_noalias],
linefmt = 'C0--') #
if freq_alias_conteo>0: # hay alias, graficar
graf_fasorn.stem(freq_n[freq_alias],ampl_n[freq_alias],
linefmt = 'C1--', label='alias')
for k in range(0,len(freq_n),1): # etiquetas de fasor
graf_fasorn.annotate(etiq_n[k],xy=(freq_n[k],ampl_n[k]),
xytext=(0,5),textcoords='offset points',
ha='center')
# etiquetas eje x usando unfactor
if un_espectro_n['freq_factor'] != sym.S.One:
unfactor = r'$'+sym.latex(un_espectro_n['freq_factor'])+'$'
freq_etiq = []
for un_num in freq_n:
freq_etiq.append(f''+str(round(un_num,4))+unfactor)
graf_fasorn.set_xticks(ticks=freq_n,labels=freq_etiq)
graf_fasorn.legend()
plt.tight_layout()
plt.show()