Ejercicio: 2Eva2001TII_T2 Contar puntos aleatorios en un triángulo
Se cuentan los puntos que caen el el área marcada en verde que se encuentra debajo de:
f(x)= -x+10siendo el intervalo [a,b] con valores de a = 0 y b=10, la mitad corresponde a (a+b)/2
Como las áreas consideradas corresponden a dos sectores, considere usar x entre[a,mitad] y entre [mitad, b], limitados en y por la línea f(x)
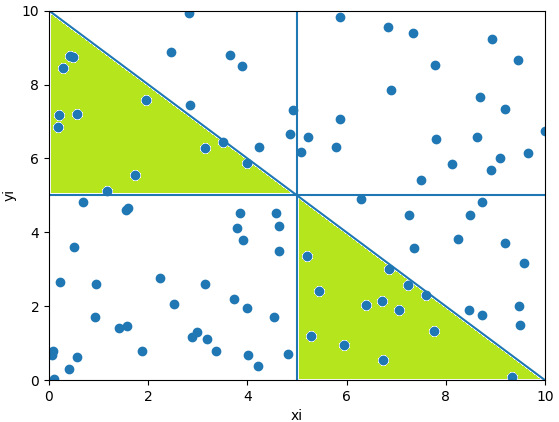
Un resultado gráfico, no requerido para el ejercicio, tan solo para mejor comprensión:
de n puntos: 100
dentro estaban: 25
>>> Algoritmo en Python
# 2Eva_IIT2001_T2 Contar puntos aleatorios
# dentro de área triángular
import random as rnd
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
n = 100
a = 0
b = 10
# función a evaluar
f = lambda x: -x+10
# PROCEDIMIENTO
mitad = (a+b)/2
X = []
Y =[]
dentro = 0
i = 0
while not(i>=n):
xi = rnd.random()*(b-a)+0
yi = rnd.random()*(b-a)+0
limite = f(xi)
if xi>mitad and yi<=limite:
dentro = dentro +1
if xi<=mitad and yi<=limite and yi>=mitad:
dentro = dentro +1
X.append(xi)
Y.append(yi)
i = i+1
# SALIDA
print(' de n puntos: ', n)
print(' dentro estaban: ', dentro)
# Grafica
plt.scatter(X,Y)
xi = np.linspace(a,b,n+1)
plt.plot(xi,f(xi))
plt.axhline(mitad)
plt.axvline(mitad)
plt.xlim(a,b)
plt.ylim(a,b)
plt.xlabel('xi')
plt.ylabel('yi')
plt.show()