1. Bases Numéricas en programación
Referencia: Van Rossum 15 p105, Rodríguez 5.6.5 p63, Sistemas de numeración
A través del tiempo la humanidad adoptado diferentes formas de numeración, tanto en símbolos como en bases.

Las formas simbólicas de numeración más conocidas son:
la arábiga (0, 1, 2, 3,… 9) usada en estos días, y
la romana (I, II, III, IV, V, VI,…X,…).
El uso de computadores nos obliga a revisar el tema de sistemas de numeración, debido a que internamente el computador opera en numeración binaria basada en dos símbolos representados como 0 y 1.

La electrónica digital, que permite construir una computadora, trabaja sobre dos estados del circuito: abierto o cerrado, verdadero o falso, 1 o 0.
Es común ver en las etiquetas de un producto el denominado código de barras que facilita el trabajo de identificar el producto vendido.
El código de barras permite usar un dispositivo para “leer” la representación binaria del producto, cada barra de color blanco o negro representa un dígito binario del número. Para estos casos es necesario disponer de un algoritmo que permita leer y convertir un código de producto de binario a decimal, así como el decimal a binario en el caso de la impresión o escritura del código de barras.
Base Numérica Decimal
La base numérica 10 nos resulta muy natural y no requiere mucha descripción. Se basa en diez símbolos conocidos como numeración arábiga: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Para números superiores a 9 se añade a la izquierda un dígito y se los combina ordenadamente: 10, 11, 12, …, 19, 20, 21, …
Al aplicar el mismo método de formación de números usando otra base numérica se obtiene resultados simulares como se muestra en la siguiente sección.
Referencias: Capítulo II Numeración. Baldor, Aurelio (1974). Aritmética de Baldor, Guatemala. Cultural Centroamericana S.A.
| posición | 3 | 2 | 1 | 0 |
| ponderación | 103 | 102 | 101 | 100 |
| peso en decimal | 1000 | 100 | 10 | 1 |
| numero decimal (1492) | 1 | 4 | 9 | 2 |
2. Número Binario a Decimal
Referencia: Baldor, Aurelio (1974), Capítulo III Otros sistemas de numeración. Aritmética de Baldor, Guatemala. Cultural Centroamericana S.A..https://es.wikipedia.org/wiki/Sistema_binario
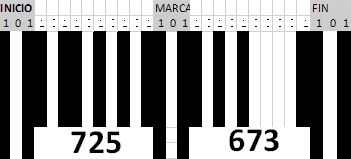
Los números binarios se conforman con los símbolos 0 y 1, que se combinan para representar cualquier número.
Una etiqueta de un producto en código de barras es la representación binaria del número que identifica el producto.
Para representar números superiores a 1 dígito, se aplica un método semejante al de formación de números decimales, combinando ordenadamente los símbolos. Se repiten las combinaciones de dígitos anteriores y se le añade un dígito para continuar la numeración
| Decimal | Binaria |
|---|---|
0 | 0 |
1 | 1 |
2 | 10 |
3 | 11 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
11 | 1011 |
12 | 1100 |
| … | … |
En el sistema binario se utiliza la ponderación por posición de dígito en la misma forma que en la numeración decimal, por ejemplo:
| posición | 3 | 2 | 1 | 0 |
| ponderación | 23 | 22 | 21 | 20 |
| peso en decimal | 8 | 4 | 2 | 1 |
| Número en binario 5(10)=101(2) =0*8+1*4+0*2+1*1 | 0 | 1 | 0 | 1 |
- La posición más a la derecha es menos significativa y de menor ponderación o peso: 20
- La siguiente posición hacia la izquierda tiene un peso equivalente a: 21
- La siguiente posición a la izquierda usa un equivalente a: 23
- Y así sucesivamente.
Se puede encontrar el valor decimal de un número binario cualquiera multiplicando el dígito correspondiente por el “peso” que tiene y sumando los resultados parciales.
Ejercicio: Convertir el binario 101 a decimal
Para convertir el número binario 101 a decimal, se realizan las operaciones de ponderación usando los residuos de la división para 10 del número en base 10.
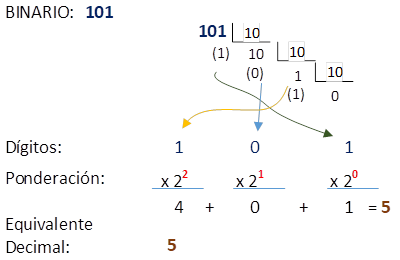
La operación de residuo es la extracción de cada dígito empezando por el menos significativo. cada dígito se pondera por 2i, siendo i la posición del dígito.
Algoritmo Binario a Decimal
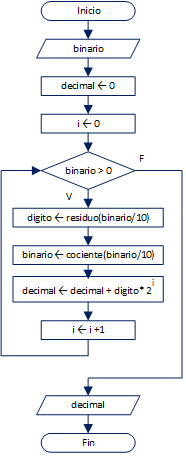
Para realizar el algoritmo, se separa cada dígito del número binario, y luego se realiza la operación de ponderación para acumularla en el resultado final.
En la ponderación se usará un contador de posición para ser usado como el exponente de la base 2.
El algoritmo en diagrama de flujo se representará como:
# Binario a Decimal
binario = int(input("número en binario: "))
decimal = 0
i = 0
while (binario>0):
digito = binario%10
binario = int(binario//10)
decimal = decimal+digito*(2**i)
i = i+1
# SALIDA
print("en decimal: ",decimal)
con los siguientes resultados:
>>>
número en binario: 101
en decimal: 5
>>>
número en binario: 1000
en decimal: 8
>>>
número en binario: 111
en decimal: 7
>>> Referencia: Cadenas de Supermercados - Gigantes de la comida. History Latinoamérica. 18 Julio 2025. minuto 8:15 códigos de barra.
3. Número Decimal a Binario

Los números decimales se convierten a base binaria para mostrarlos por ejemplo en códigos de barra.
La base numérica binaria es ampliamente usada en informática o computación.
Ejercicio: Cinco en binario
Para convertir el número Decimal 5 en Binario hay que descomponer el número en la nueva base numérica, para luego trabajar con los residuos y ubicar cada uno desde la posición menos significativa a la más significativa.
Las operaciones se basan principalmente en el uso de cocientes, residuos y acumuladores y el proceso se muestra en la figura:
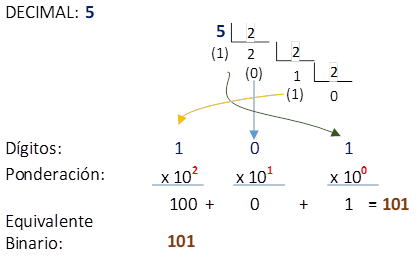
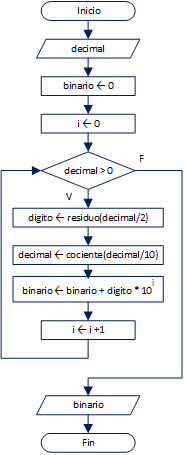
Observe la diferencia en las operaciones para el divisor y la base, las operaciones son similares a las del ejercicio de Binario a Decimal.
Cambia el divisor y la ponderación usadas, sin embargo las operaciones seguirán siendo básicamente las mismas.
Con esta observación se pueden plantear los cambios de base con otras bases numéricas, por ejemplo la de base 8 también conocida como Octal.
Algoritmo Decimal a Binario
Puesto que el ejercicio es una variante del mostrado como Binario a Decimal, se muestra directamente su forma en: Diagrama de flujo, pseudo-código y en Python.
El ejemplo en seudo-código:
Proceso DecimalBinario
Leer decimal
binario ← 0
i ← 0
Mientras decimal > 0
digito ← decimal mod 2
decimal ← trunc(decimal/2)
binario ← binario+digito*10^i
i ← i + 1
FinMientras
Escribir binario
FinProcesoAlgoritmo en Python
# Decimal a binario
# INGRESO
decimal = int(input("número decimal: "))
# PROCEDIMIENTO
binario = 0
i = 0
while (decimal>0):
digito = decimal%2
decimal = int(decimal//2)
binario = binario+digito*(10**i)
i = i+1
# SALIDA
print("en binario: ",binario)
Resultados en Python
número decimal:5
en binario: 101
>>>4. Ejercicios
1. Realizar los algoritmos Binario a Decimal y Decimal a Binario usando el lazo Repita-Hasta.
2. Crear un algoritmo para convertir un número de base numérica x a base y. Comprobar el algoritmo usando los valores: 23x númeroy.
Sugerencia, convierta el número de la base x primero a decimal y luego transforme el resultado a la siguiente base numérica y.