1ra Evaluación 2024-2025 PAO I. 2/Julio/2024
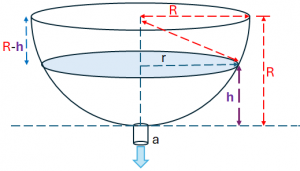
Tema 1. (30 puntos) Un reservorio semiesférico de radio R = 3 m, está lleno agua hasta la altura h como se muestra en la figura. En la base tiene un tubo de salida con abertura de área a = 0.01 m2. El coeficiente de fricción hidráulico K = 0.85 g = 9.8 m/s2.
Se requiere que el reservorio se vacíe en menos de tf = 15 min.
La ecuación diferencial para el vaciado de tanques es:
Considerando la relación de la altura del líquido h con
respecto al radio R de la semiesfera: r^2 + \Big( R-h\Big)^2 = R^2
Y el Área del círculo en función de h: A(h) = \pi \Big(2Rh -h^2 \Big)
se encuentra la solución general en la expresión:
\frac{4}{3}R \Big(h_f^{3/2} - h_0^{3/2} \Big) - \frac{2}{5}\Big(h_f^{5/2} - h_0^{5/2} \Big) = \frac{Ka}{\pi}\sqrt{2g}\Big(t_0-t_f \Big)Dado que se vacía el reservorio, hf = 0 y que el experimento inicia en t0=0, h0 =h y tf=t, la expresión se simplifica:
-\frac{4}{3}R h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{Ka}{\pi} t \sqrt{2g}
a. Plantear el ejercicio para encontrar h para un t dado, muestre el intervalo de búsqueda y una gráfica.
b. Desarrolle usando el método de Newton-Raphson para tres iteraciones y tolerancia milimétrica.
c. Verifique el orden de convergencia y observe sus resultados usando el algoritmo.
Nota: la gravedad g tiene unidades de segundos, el tiempo de vaciado está en minutos.
Rúbrica: Planteamiento (5 puntos), iteraciones y error (15 puntos), análisis de la convergencia (5 puntos). observación de resultados, algoritmo y gráficas adjuntos (5 puntos).
Referencia:
[1] Ejercicio 25.21 p765 y 5.17. p143 Steven C. Chapra. Numerical Methods 7th Edition.
[2] Vaciado de un tanque semiesférico. Tiempo total de vaciado. Demostración y aplicación. Sebastian Rodriguez