[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..
Método de la Secante
Referencia: Chapra 6.3 p154, Burden 2.3 p54,
El método de la secante busca evitar un posible inconveniente en el desarrollo el algoritmo para método de Newton-Raphson, que es el implementar la evaluación de la expresión de la primera derivada.
La derivada de la función f(x) también se puede aproximar mediante una diferencia finita dividida hacia atrás:
f'(x_i) = \frac{f(x_{i-1})-f(x_i)}{x_{i-1}-x_i}la que se sustituye en la ecuación del método de Newton-Raphson para obtener:
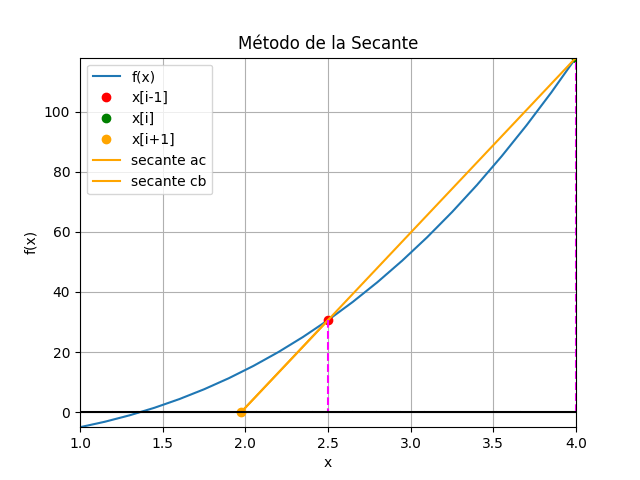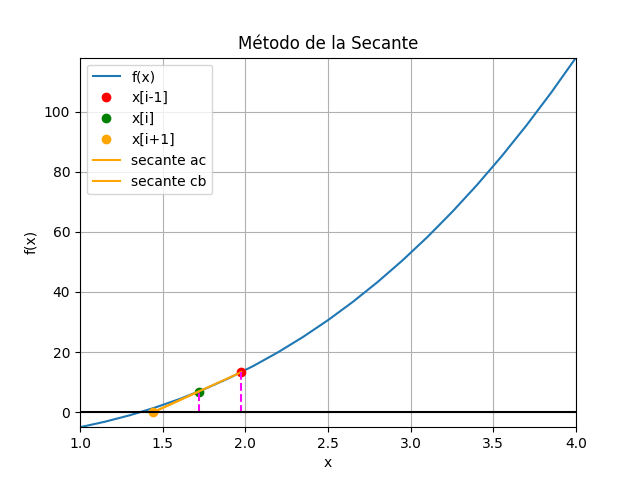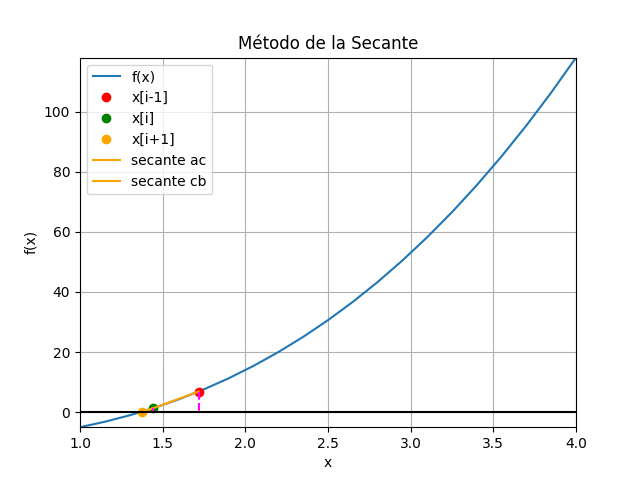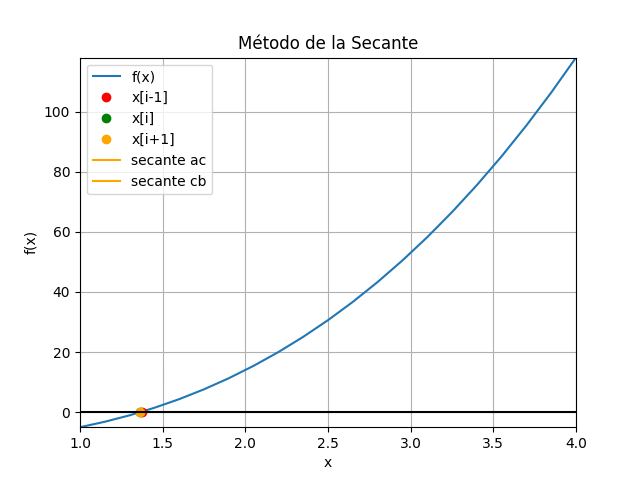
x_{i+1}= x_i - f(x_i)\frac{(x_{i-1} - x_i)}{f(x_{i-1}) - f(x_i)}Los métodos de la secante y de la falsa posición tienen ecuaciones idénticas, usan dos valores iniciales x[i-1] , x[i], para proyectar el nuevo valor de x[i+1].
Sin embargo, existe una diferencia importante entre ambos métodos en la forma en que uno de los valores iniciales se reemplaza por la nueva aproximación.
En el método de la falsa posición, la última aproximación de la raíz reemplaza cualquiera de los valores iniciales que dé un valor de la función con el mismo signo. En consecuencia, las dos aproximaciones siempre encierran a la raíz, es un método cerrado y siempre converge.
En el método de la secante se reemplaza los valores en secuencia estricta: xi reemplaza a x[i – 1], con el nuevo valor x[i+1] se reemplaza a xi . Por lo que, algunas veces los dos valores están en el mismo lado de la raíz y en ciertos casos esto puede llevar a divergencias.
Observación: ¿Cuál es la diferencia con el método de Newton-Raphson?
[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
Recta Secante para la gráfica
Si se quiere dibujar la recta secante, se inicia con la ecuación de la recta usando el valor de la pendiente del triángulo presentado en la gráfica del método, cambie la constante b por b0.
y = mx + bPara identificar los puntos consecutivos con variables simples, se usa la siguiente conversión
| xi-1 | xi | xi+1 |
| xa | xb | xc |
Se usa un punto conocido, por ejemplo (xb,fb) y se encuentra b0
f(x_b) = m x_b + b_0 f(x_b) - m x_b = b_0reordenando, se usan tres expresiones para disponer de la función de la recta secante.
m = \frac{f(x_a)-f(x_b)}{x_a-x_b} b_0 = f(x_b) - m x_b rsc(x)= m x + b_0[ Secante ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]