2Eva_2024PAOII_T3 EDP Elíptica con función en borde superior

2da Evaluación 2024-2025 PAO II. 28/Enero/2025

Tema 3. (35 puntos) Considere la ecuación diferencial parcial, tipo elíptica descrita sobre una placa en el plano x,y:

$\frac{\partial ^2 u}{\partial x^2} = -\frac{\partial ^2 u}{\partial y^2}$

0≤x≤1 ; 0≤y≤1.5

Con condiciones en frontera en los intervalos definidos para una placa.

u(0, y) = 0 ; u(1, y) = 0

u(x, 0) = 0

u(x, 1.5) = 100 sin(πx)

Utilice diferencias finitas para las variables independientes x,y

a. Plantee las ecuaciones discretas a usar un método numérico en un nodo i,j

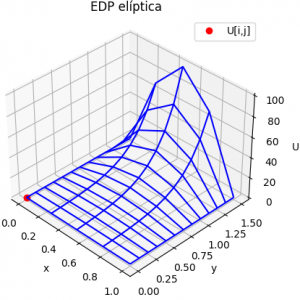
b. Realice la gráfica de malla, detalle los valores de i, j, x_i, y_j

c. Desarrolle y obtenga el modelo discreto para u(x_i,y_j)

d. Determine el valor de Lambda λ, considerando Δx = 1/4 , Δy = 1/8

e. Desarrolle la ecuación para al menos tres nodos i,j diferentes y consecutivos.

f. (Extra) Estime el error de u(x_i,t_j) y adjunte los archivos del algoritmo.py, resultados.txt, gráficas.png

Rúbrica: Selección de diferencias finitas divididas (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (5 puntos), literal e (15 puntos). literal f extra (5 puntos)

Referencia: Chapter 13: Partial Differential Equations (Part 2 – Elliptic PDEs). Lindsey Westover. 18 Marzo 2021. https://youtu.be/0eI5zrhtEjE?si=a8rQhpEEirvMBC26&t=633