2da Evaluación 2025-2026 PAO I. 26/Agosto/2025
Tema 1 (35 puntos) Un centroide es un promedio ponderado, como el centro de gravedad, pero ponderado con una propiedad geométrica como el área o el volumen, y no con una propiedad física como el peso o la masa. 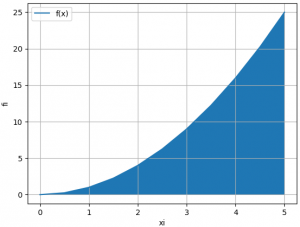
Esto significa que los centroides son propiedades de formas puras, no de objetos físicos. Para el caso particular dado en f(x), los resultados de los integrales permiten obtener las coordenadas del punto medio:
| \bar{x} = \frac{Q_y}{A} | \bar{y} = \frac{Q_x}{A} |
| Q_y = \int x dA = \int_0^5 x^3 dx | Q_x = \int ydA = \int_0^5 \frac{x^4}{2} dx |
| A = \int f(x) dx = \int_0^5 x^2 dx |
Donde Qx, Qy corresponden al primer momento de área con respecto a cada eje. Realice el planteamiento de los integrales considerando que:
a. Para el integral con Qy use fórmulas de Simpson con al menos 3 tramos, mientras que
b. Para el integral con Qx use Cuadratura de Gauss de dos puntos.
c. Desarrolle las expresiones completas del ejercicio para cada función. Para A seleccione el método numérico de su preferencia.
d. Indique el resultado obtenido para el integral requerido y la cota de error.
e. Determine las coordenadas del centroide según las fórmulas presentadas.
f. Adjunte algoritmo.py, resultado.txt y gráfica.png.
Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos), literal f (5 puntos)
Referencia: [1] Engineering Statics Open and Interactive. Daniel W. Baker, William Haynes. https://engineeringstatics.org/Chapter_07-centroids.html
[2] Centroide de una parábola mediante integración. Ingeniería elemental. 13 octubre 2022.
