[ Gauss-Jordan ] [ Ejercicio ] [ Eliminación atrás ] [ Algoritmo ] [ función ]
..
1. Método de Gauss-Jordan
Referencia: Chapra 9.7 p277, Burden 9Ed Ex6.1.12 p370, Rodríguez 4.2 p106
El método de Gauss-Jordan presenta un procedimiento alterno al de "sustitución hacia atrás" realizado para el método de Gauss. Luego de obtener la "matriz triangular superior", aplica el procedimiento de "Eliminación hacia atrás".
\left( \begin{array}{rrr|r} a_{0,0} & a_{0,1} & a_{0,2} & b_{0} \\ 0 & a_{1,1} & a_{1,2} & b_{1} \\ 0 & 0 & a_{2,2} & b_{2} \end{array} \right)- Eliminación hacia atrás
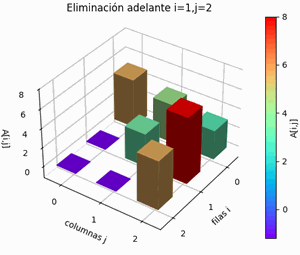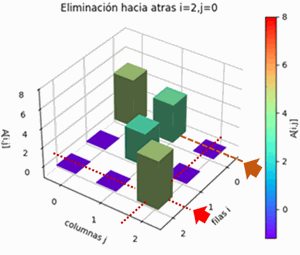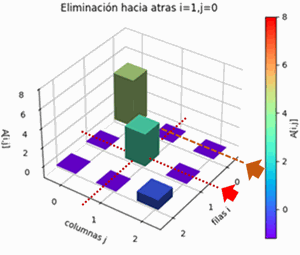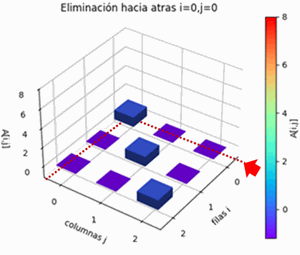Desde la última fila,
para i = n-1, n-2, ...
sobre las filas k = i-1 superiores
Se mantienen al inicio los procedimientos para:
matriz aumentada,
pivoteo parcial por filas,
eliminación hacia adelante desarrollados anteriormente.
[ Gauss-Jordan ] [ Ejercicio ] [ Eliminación atrás ] [ Algoritmo ] [ función ]
..
2. Ejercicio
Referencia: Rodríguez 4.0 p105, 1Eva_IT2010_T3_MN Precio artículos
\begin{cases} 4x_1+2x_2+5x_3 = 60.70 \\ 2x_1+5x_2+8x_3 = 92.90 \\ 5x_1+4x_2+3x_3 = 56.30 \end{cases}
Se continúa con el ejercicio desarrollado para el método de Gauss desde la "matriz triangular superior",
luego de eliminación hacia adelante:
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]
[ Gauss-Jordan ] [ Ejercicio ] [ Eliminación atrás ] [ Algoritmo ] [ función ]
..
3. Eliminación hacia atrás
El procedimiento es semejante al realizado para "eliminación hacia adelante", con la diferencia que se inicia en la última fila hacia la primera. Para el ejercicio presentado se tiene que:
utlfila = n-1 = 3-1 = 2 ultcolumna = m-1 = 4-1 = 3
iteración 1, operación fila 3 y 2
Se aplica desde la última fila i, para las otras filas k que se encuentran hacia atrás.
i = ultfila = 2 pivote = AB[2,2] = 5 k = i-1 # hacia atrás
se realizan las operaciones entre las filas i y la fila j
[0. 3.4 6.8 70.38] -(6.8/5)*[0. 0. 5. 40.5 ] _______________________________ = [0.0 3.4 8.8e-16 15.3]
para reemplazar los valores de la segunda fila en la matriz aumentada
[[5.0 4.0 3.0 56.3]
[0.0 3.4 8.8e-16 15.3]
[0.0 0.0 5.0 40.5]]
Observe que hay un valor muy pequeño del orden de 8.8x10-16, que para las otras magnitudes se puede considerar como casi cero.
iteración 2, operación fila 3 y 1
Se calculan los nuevos valores de índice k
k = k-1 = 2-1 = 1 # hacia atrás
se realizan las operaciones entre las filas i y la fila j
[5.0 4.0 3.0 56.3] -(3/5)*[0.0 0.0 5.0 40.5] __________________________________ = [5.0 4.0 0.0 32.0]
que al actualizar la matriz aumentada se tiene:
[[5.0 4.0 0.0 32.0]
[0.0 3.4 8.8e-16 15.3]
[0.0 0.0 5.0 40.5]]}
Al haber terminado las filas hacia arriba, 
se puede así determinar el valor de x3 al dividir la fila 3 para el pivote
[[5.0 4.0 0.0 32.0] [0.0 3.4 8.8e-16 15.3] [0.0 0.0 1.0 8.1]]}
iteración 3, operación fila 2 y 1
se actualizan los valores de los índices:
i = i-1 = 2-1 = 1 k = i-1 = 1-1 = 0
se pueden realizar operaciones en una sola fila hacia atrás, por lo que el resultado hasta ahora es:
[5.0 4.0 0.0 32.0] -(4/3.4)*[0.0 3.4 8.8e-16 15.3] __________________________________ = [5.0 0.0 -1.04e-15 14.0] [[ 5.0 0.0 -1.04e-15 14.0] [ 0.0 3.4 8.8e-16 15.3] [ 0.0 0.0 1.0 8.1]]
Se obtiene el valor de x2,
dividiendo para el valor del pivote,
[[ 5.0 0.0 -1.04e-15 14.0] [ 0.0 1.0 2.6e-16 4.5] [ 0.0 0.0 1.0 8.1]]
iteración 4, operación fila 1
No hay otras filas con las que iterar,
por lo que solo se obtiene el valor de x1 al dividir para el pivote.
[[ 1.0 0.0 -2.08e-15 2.8] [ 0.0 1.0 2.6e-16 4.5] [ 0.0 0.0 1.0 8.1]]
La solución del sistema de ecuaciones se presenta como una matriz identidad concatenada a un vector columna de constantes.
solución X: [2.8, 4.5, 8.1]X= [2.8, 4.5 , 8.1 ]
Observación: en la matriz hay unos valores del orden de 10-16, que corresponden a errores de operaciones en computadora (truncamiento y redondeo) que pueden ser descartados por ser casi cero. Hay que establecer entonces un parámetro para controlar los casos en que la diferencia entre los ordenes de magnitud son por ejemplo menores a 15 ordenes de magnitud 10-15. e implementarlo en los algoritmos.
[ Gauss-Jordan ] [ Ejercicio ] [ Eliminación atrás ] [ Algoritmo ] [ función ]
..
4. Algoritmo en Python
Esta sección reutiliza el algoritmo desarrollado para el Método de Gauss, por lo que los bloques de procedimiento son semejantes hasta eliminación hacia adelante. Se añade el procedimiento de eliminación hacia atrás para completar la solución al sistema de ecuaciones.
Instrucciones en Python
# Método de Gauss-Jordan # Sistemas de Ecuaciones A.X=B import numpy as np # INGRESO A = [[4,2,5], [2,5,8], [5,4,3]] B = [60.70, 92.90, 56.30] # PROCEDIMIENTO np.set_printoptions(precision=4) # 4 decimales en print casicero = 1e-15 # redondear a cero # Matrices como arreglo, numeros reales A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada AB B_columna = np.transpose([B]) AB = np.concatenate((A,B_columna),axis=1) # Pivoteo parcial por filas tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = abs(AB[i:,i]) dondemax = np.argmax(columna) if (dondemax !=0): # NO en diagonal # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal print('Pivoteo parcial por filas AB: ----') print(AB) # Eliminación hacia adelante print('Eliminación hacia adelante: ------') for i in range(0,n-1,1): # una fila pivote = AB[i,i] adelante = i + 1 for k in range(adelante,n,1): # diagonal adelante factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - AB[i,:]*factor print('i:',i,'k:',k, 'factor:',factor) print(AB) # Eliminación hacia atras print('Eliminación hacia atras: ------') ultfila = n-1 ultcolumna = m-1 for i in range(ultfila,0-1,-1): # una fila pivote = AB[i,i] print('i:',i,' pivote:',pivote) atras = i - 1 for k in range(atras,0-1,-1): # diagonal adelante factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - AB[i,:]*factor for j in range(0,m,1): # casicero revisa if abs(AB[k,j])<casicero: AB[k,j]=0 print(' k:',k, 'factor:',factor) print(AB) AB[i,:] = AB[i,:]/AB[i,i] # diagonal a unos print('AB:') print(AB) X = np.copy(AB[:,ultcolumna]) # SALIDA print('Método de Gauss-Jordan') print('solución X: ') print(X)
El resultado del algoritmo es:
Pivoteo parcial por filas AB: ---- [[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]] Eliminación hacia adelante: ------ i: 0 k: 1 factor: 0.4 i: 0 k: 2 factor: 0.8 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. -1.2 2.6 15.66]] i: 1 k: 2 factor: -0.3529411764705883 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]] Eliminación hacia atras: ------ i: 2 pivote: 5.0 k: 1 factor: 1.3599999999999999 k: 0 factor: 0.6 [[ 5. 4. 0. 32. ] [ 0. 3.4 0. 15.3] [ 0. 0. 5. 40.5]] i: 1 pivote: 3.4 k: 0 factor: 1.1764705882352942 [[ 5. 0. 0. 14. ] [ 0. 3.4 0. 15.3] [ 0. 0. 1. 8.1]] i: 0 pivote: 5.0 [[ 5. 0. 0. 14. ] [ 0. 1. 0. 4.5] [ 0. 0. 1. 8.1]] AB: [[1. 0. 0. 2.8] [0. 1. 0. 4.5] [0. 0. 1. 8.1]] Método de Gauss-Jordan solución X: [2.8 4.5 8.1]
[ Gauss-Jordan ] [ Ejercicio ] [ Eliminación atrás ] [ Algoritmo ] [ función ]
..
5. Algoritmo como función en Python
El algoritmo considera que valores con magnitud menores a "casicero" se redondean a 0. Se aplica recorriendo la fila de referencia k, por cada elemento j.
# redondeo a cero for j in range(0,m,1): if np.abs(AB[k,j])<=casicero: AB[k,j]=0
Adicionalmente se añade el parámetro "inversa", que se usa para encontrar A-1 como se indica en Matriz Inversa.
Con el algoritmo se obtiene el siguiente resultado:
Matriz aumentada [[ 4. 2. 5. 60.7] [ 2. 5. 8. 92.9] [ 5. 4. 3. 56.3]] Pivoteo parcial: 1 intercambiar filas: 0 y 2 [[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]] Elimina hacia adelante: fila i: 0 pivote: 5.0 fila k: 1 factor: 0.4 fila k: 2 factor: 0.8 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. -1.2 2.6 15.66]] fila i: 1 pivote: 3.4 fila k: 2 factor: -0.3529411764705883 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]] fila i: 2 pivote: 5.0 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]] Elimina hacia Atrás: fila i: 2 pivote: 5.0 fila k: 1 factor: 1.3599999999999999 fila k: 0 factor: 0.6 [[ 5. 4. 0. 32. ] [ 0. 3.4 0. 15.3] [ 0. 0. 1. 8.1]] fila i: 1 pivote: 3.4 fila k: 0 factor: 1.1764705882352942 [[ 5. 0. 0. 14. ] [ 0. 1. 0. 4.5] [ 0. 0. 1. 8.1]] fila i: 0 pivote: 5.0 [[1. 0. 0. 2.8] [0. 1. 0. 4.5] [0. 0. 1. 8.1]] solución X: [2.8 4.5 8.1]
Instrucciones en Python
# Método de Gauss-Jordan # Sistemas de Ecuaciones A.X=B import numpy as np def gauss_eliminaAtras(AB, vertabla=False, inversa=False, casicero = 1e-15): ''' Gauss-Jordan elimina hacia atrás Requiere la matriz triangular inferior Tarea: Verificar que sea triangular inferior ''' tamano = np.shape(AB) n = tamano[0] m = tamano[1] ultfila = n-1 ultcolumna = m-1 if vertabla==True: print('Elimina hacia Atrás:') for i in range(ultfila,0-1,-1): pivote = AB[i,i] atras = i-1 # arriba de la fila i if vertabla==True: print(' fila i:',i,' pivote:', pivote) for k in range(atras,0-1,-1): if np.abs(AB[k,i])>=casicero: factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - factor*AB[i,:] # redondeo a cero for j in range(0,m,1): if np.abs(AB[k,j])<=casicero: AB[k,j]=0 if vertabla==True: print(' fila k:',k, ' factor:',factor) else: print(' pivote:', pivote,'en fila:',i, 'genera division para cero') AB[i,:] = AB[i,:]/AB[i,i] # diagonal a unos if vertabla==True: print(AB) respuesta = np.copy(AB[:,ultcolumna]) if inversa==True: # matriz inversa respuesta = np.copy(AB[:,n:]) return(respuesta) def gauss_eliminaAdelante(AB,vertabla=False, lu=False,casicero = 1e-15): ''' Gauss elimina hacia adelante tarea: verificar términos cero ''' tamano = np.shape(AB) n = tamano[0] m = tamano[1] if vertabla==True: print('Elimina hacia adelante:') for i in range(0,n,1): pivote = AB[i,i] adelante = i+1 if vertabla==True: print(' fila i:',i,' pivote:', pivote) for k in range(adelante,n,1): if (np.abs(pivote)>=casicero): factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - factor*AB[i,:] for j in range(0,m,1): # casicero revisa if abs(AB[k,j])<casicero: AB[k,j]=0 if vertabla==True: print(' fila k:',k, ' factor:',factor) else: print(' pivote:', pivote,'en fila:',i, 'genera division para cero') if vertabla==True: print(AB) respuesta = np.copy(AB) if lu==True: # matriz triangular A=L.U U = AB[:,:n-1] respuesta = [AB,L,U] return(respuesta) def pivoteafila(A,B,vertabla=False): ''' Pivotea parcial por filas Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) if vertabla==True: print('Matriz aumentada') print(AB) print('Pivoteo parcial:') # Pivoteo por filas AB tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax+i) if vertabla==True: if pivoteado==0: print(' Pivoteo por filas NO requerido') else: print('AB:') print(AB) return(AB) # PROGRAMA ------------------------ # INGRESO A = [[4,2,5], [2,5,8], [5,4,3]] B = [60.70,92.90,56.30] # PROCEDIMIENTO np.set_printoptions(precision=4) # 4 decimales en print casicero = 1e-15 # redondear a cero AB = pivoteafila(A,B,vertabla=True) AB = gauss_eliminaAdelante(AB,vertabla=True) X = gauss_eliminaAtras(AB,vertabla=True) # SALIDA print('solución X: ') print(X)
Tarea
implementar caso cuando aparecen ceros en la diagonal para dar respuesta, convertir a funciones cada parte
[ Gauss-Jordan ] [ Ejercicio ] [ Eliminación atrás ] [ Algoritmo ] [ función ]