Ejercicio: 1Eva_IIT2010_T1 Aproximar con polinomio
Desarrollo Analítico
Encabezado ejemplo para el desarrollo con Papel y lápiz:
Opción 1. Usando el polinomio de Taylor
Usando Unidad 1 Polinomio de Taylor, supondremos que: x0=0
El polinomio de Taylor requerido es de: grado 2
P_{n}(x) = f(x_0)+\frac{f'(x_0)}{1!} (x-x_0) +
+ \frac{f''(x_0)}{2!}(x-x_0)^2 +
Se escribe la función f(x) y sus derivadas para el polinomio:
f(x) = e^x \cos (x) +1
primera derivada
f'(x) = e^x \cos (x) - e^x \sin(x)
f'(x) = e^x (\cos (x) - \sin(x))
segunda derivada
f''(x) = e^x( \cos (x) - \sin(x))+
+ e^x (-\sin(x) - \cos(x))
f''(x) = -2 e^x \sin(x))
Punto de referencia x0 = 0, tomado como ejemplo dentro del intervalo.
Observación: escriba las expresiones, reemplazando los valores. Un criterio de evaluación es que, si en la lección o examen no tuvo tiempo para usar la calculadora, se puede evaluar si realizaba las operaciones con el punto de referencia y expresiones correctas.
f(0) = e^0 \cos (0) +1 = 2
f'(0) = e^0(\cos (0) - \sin(0)) = 1
f''(0) = -2 e^0 \sin(0)) = 0
Sustitución en el polinomio de Taylor planteado:
p_2(x) = f(x_0) + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2
P_{2}(x) = 2+\frac{1}{1} (x-0) +
+ \frac{0}{2}(x-0)^2 +
P_{2}(x) = 2+ x
El error referenciado a los otros puntos será:
errado = |f(x)-p(x)|
errado = \Big|\Big( e^x \cos (x) +1 \Big) - (2+ x)\Big|
usando un punto diferente a x0=0, como x = π/2
errado = \Big| \Big( e^{\frac{\pi}{2}}\cos \Big( \frac{\pi}{2} \Big) +1 \Big) - \Big(2+ \frac{\pi}{2}\Big) \Big|
errado = | 1 - 3.5707| = 2.5707
Tarea: calcular el error, para x = π, verificando que pase por los puntos requeridos.
Opción 2. Usando el polinomio de interpolación
Siguiendo la unidad 4 para interpolación, el polinomio requerido tiene la forma:
p(x) = a + bx + cx^2
por lo que conociendo los pares ordenados por donde debe pasar se puede plantear las ecuaciones y encontrar a,b,c.
f(0) = e^0 \cos (0) +1 = 2
f(\pi/2) = e^{\pi/2} \cos (\pi /2) +1 = 1(0)+1 =1
f(\pi) = e^{\pi} \cos (\pi) +1 = e^{\pi} +1
se encuentra que a = 2 cuando x = 0 y que reemplazando los valores de x =π/2 y x=π se tiene:
2 + (π/2) b + (π/2)2 c = 1
2 + π b + (π)2 c = eπ +1
que se convierte en:
(π/2) b + (π/2)2 c = -1
π b + (π)2 c = -(eπ +1)
al multiplicar la primera ecuación por 2 y restando de la segunda
- π2/2 c = eπ -1
c = (-2/π2)(eπ -1)
y sustituir c en la segunda ecuación:
π b + (π)2 (-2/π2)(eπ -1) = -(eπ +1)
π b = -(eπ +1) + 2(eπ -1) = -eπ -1 + 2eπ -2
b = (eπ -3)/π
El polinomio resultante es:
p(x) = 2 + \frac{e^{\pi}-3}{\pi}x + \frac{-1(e^{\pi}-1)}{\pi ^2}x^2
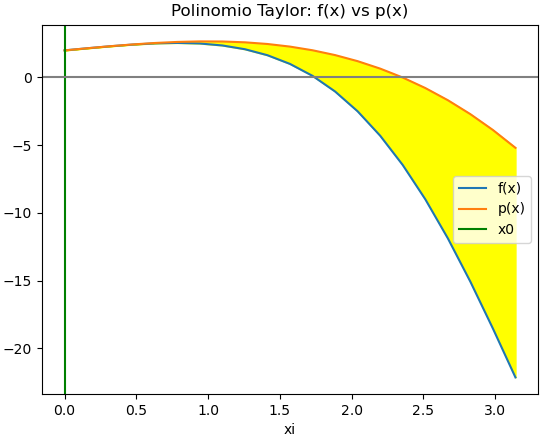
Probando respuesta con los valores en la función y polinomio usando Python, se encuentra que el polinomio pasa por los puntos. Al observar la gráfica observa que se cumple lo requerido pero visualiza el error de aproximación usando el método de la opción 2.

Algoritmo con Python
Algoritmo desarrollado en clase, usado como taller, modificado para el problema planteado.
Observación: Se reordena el algoritmo para mantener ordenados y separados los bloques de ingreso, procedimiento y salida. Así los bloques pueden ser convertidos fácilmente a funciones algorítmicas def-return.
Observe que la variable n se interprete correctamente como "términos" o "grados" del polinomio de Taylor.
# Aproximación Polinomio de Taylor alrededor de x0
# f(x) en forma simbólica con sympy
import numpy as np
import math
import sympy as sym
import matplotlib.pyplot as plt
# INGRESO --------------------
x = sym.Symbol('x')
fx = sym.exp(x)*sym.cos(x) + 1
x0 = 0
n = 3 # grado de polinomio
# Intervalo para Gráfica
a = 0
b = np.pi
muestras = 21
# PROCEDIMIENTO -------------
# construye polinomio Taylor
k = 0 # contador de términos
polinomio = 0
while (k <= n):
derivada = fx.diff(x,k)
derivadax0 = derivada.subs(x,x0)
divisor = math.factorial(k)
terminok = (derivadax0/divisor)*(x-x0)**k
polinomio = polinomio + terminok
k = k + 1
# forma lambda para evaluación numérica
fxn = sym.lambdify(x,fx,'numpy')
pxn = sym.lambdify(x,polinomio,'numpy')
# evaluar en intervalo para gráfica
xi = np.linspace(a,b,muestras)
fxi = fxn(xi)
pxi = pxn(xi)
# SALIDA --------------------
print('polinomio p(x)=')
print(polinomio)
print()
sym.pprint(polinomio)
# Gráfica
plt.plot(xi,fxi,label='f(x)')
plt.plot(xi,pxi,label='p(x)')
# franja de error
plt.fill_between(xi,pxi,fxi,color='yellow')
plt.xlabel('xi')
plt.axvline(x0,color='green', label='x0')
plt.axhline(0,color='grey')
plt.title('Polinomio Taylor: f(x) vs p(x)')
plt.legend()
plt.show()
Resultado del algoritmo
Revisar si el polinomio es concordante con lo realizado a lápiz y papel, de no ser así revisar el algoritmo o los pasos realizados en papel, deben ser iguales.
Comprobando que el algoritmo esté correcto y pueda ser usado en otros ejercicios.
polinomio p(x)=
-x**3/3 + x + 2
3
x
- -- + x + 2
3
Resultados gráficos para x0=0
Continuar con el ejercicio con x0 = π y luego con el siguiente punto x0 = π/2.
Comparar resultados y presentar: Observaciones y recomendaciones semejantes a las indicadas durante el desarrollo de la clase.