Ejercicio: 2Eva_2024PAOI_T1 EDO Salto Bungee tiempo extiende cuerda
 Como referencia par el ejercicio, solo se realizará la primera parte, acorde a:
Como referencia par el ejercicio, solo se realizará la primera parte, acorde a:
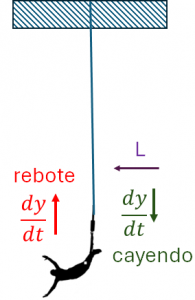
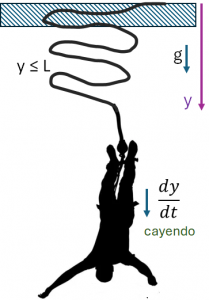
Encuentre el tiempo tc y la velocidad de la persona cuando se alcanza la longitud de la cuerda extendida y sin estirar (30 m), es decir y<L, aún se entra cayendo signo(v)=1. (solo primera ecuación)
\frac{d^2y}{dt^2} = g - signo(v) \frac{C_d}{m}\Big( \frac{dy}{dt}\Big)^2 y \leq LSuponga que las condiciones iniciales son:
y(0) = 0
\frac{dy(0)}{dt} = 0literal a
Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden
\frac{d^2y}{dt^2} = 9.8 - signo(v) \frac{0.25}{68.1}\Big( \frac{dy}{dt}\Big)^2Usando los valores de las constantes g, Cd, m, haciendo el cambio de variable dy/dt=v. Adicionalmente, en la caída inicial, signo(v)=1 y se mantiene constante hasta el 2do tramo con la cuerda estirada.
v' = 9.8 - \frac{0.25}{68.1} v^2Se plantea el ejercicio como Runge-Kutta para 2da derivada
v = y' = f(t,y,v) v' = g(t,y,v) = 9.8 - \frac{0.25}{68.1} v^2siendo h=0.5, las iteraciones se realizan como:
K_{1y} = 0.5 v K_{1v} = 0.5 \Big( 9.8 - \frac{0.25}{68.1} v^2\Big) K_{2y} = 0.5 \Big( v_i + K_{1v}\Big) K_{2v} = 0.5 \Big(9.8 - \frac{0.25}{68.1}(v_i + K_{1v})^2 \Big) y_{i+1}=y_i+\frac{K_{1y}+K_{2y}}{2} v_{i+1}=v_i+\frac{K_{1v}+K_{2v}}{2} t_{i+1} = t_i +0.5literal b
Desarrolle tres iteraciones para y(t) con tamaño de paso h=0.5
itera = 0
K_{1y} = 0.5 (0) = 0 K_{1v} = 0.5 \Big( 9.8 - \frac{0.25}{68.1} (0)^2\Big) = 4.9 K_{2y} = 0.5 ( 0 + 4.9) = 2.45 K_{2v} = 0.5 \Big(9.8 - \frac{0.25}{68.1}(0 + 2.45)^2 \Big) =4.8559 y_{i+1}=0+\frac{0+2.45}{2}=1.225 v_{i+1}=0+\frac{4.9+4.8889}{2}=4.8779 t_{i+1} =0 +0.5 = 0.5itera=1
...
Continuar con las iteraciones como tarea.
literal c
Usando el algoritmo, aproxime la solución para y en el intervalo entre [0,tc], adjunte sus resultados.txt
las iteraciones con el algoritmo son:
[ ti, yi, vi,K1y,K1v,K2y,K2v] [[0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00] [5.000000e-01 1.225000e+00 4.877964e+00 0.000000e+00 4.900000e+00 2.450000e+00 4.855929e+00] [1.000000e+00 4.878063e+00 9.669162e+00 2.438982e+00 4.856324e+00 4.867144e+00 4.726071e+00] [1.500000e+00 1.089474e+01 1.429311e+01 4.834581e+00 4.728391e+00 7.198776e+00 4.519513e+00] [2.000000e+00 1.917255e+01 1.868062e+01 7.146557e+00 4.525013e+00 9.409063e+00 4.249997e+00] [2.500000e+00 2.957773e+01 2.277738e+01 9.340309e+00 4.259461e+00 1.147004e+01 3.934054e+00] [3.000000e+00 4.195334e+01 2.654573e+01 1.138869e+01 3.947708e+00 1.336254e+01 3.589005e+00]
con lo que se observa que para alcanzar los 30m de la cuerda sin estirar se alcanzan entre los [2.5, 3.0] s.
literal d
Indique el valor de tc, muestre cómo mejorar la precisión y realice sus observaciones sobre los resultados.
Para mejorar la precisión del algoritmo se reduce el valor del tamaño de paso h, de esta forma se puede obtener una mejor lectura del tiempo de la primera fase del ejercicio.
Por ejemplo haciendo el tamaño de paso h=0.5/4, el tiempo entre [2.5, 2.625]. que tiene un error segundos menor al valor encontrado inicialmente y se mejora la precisión.