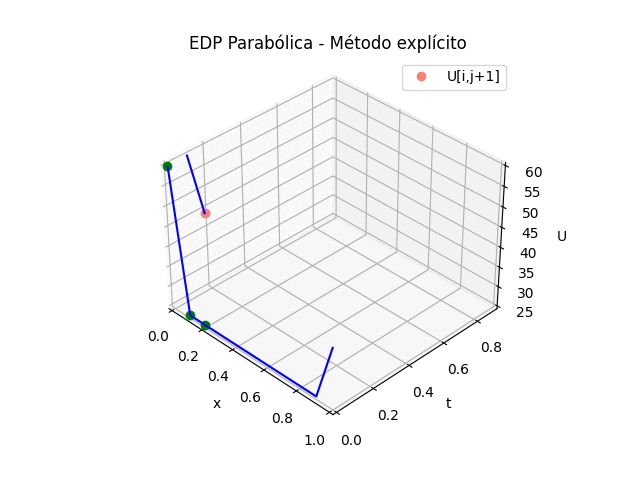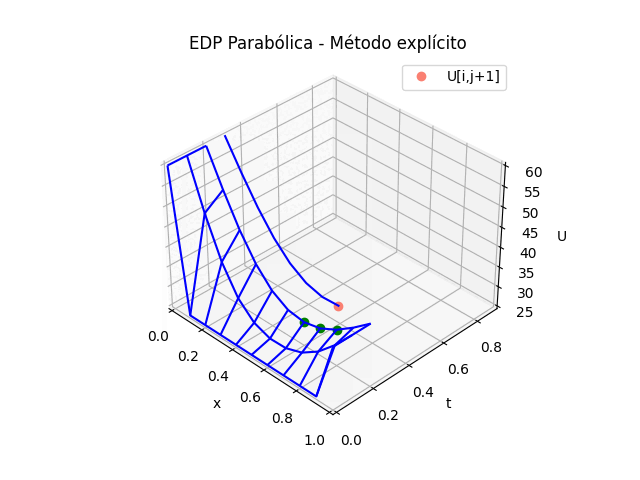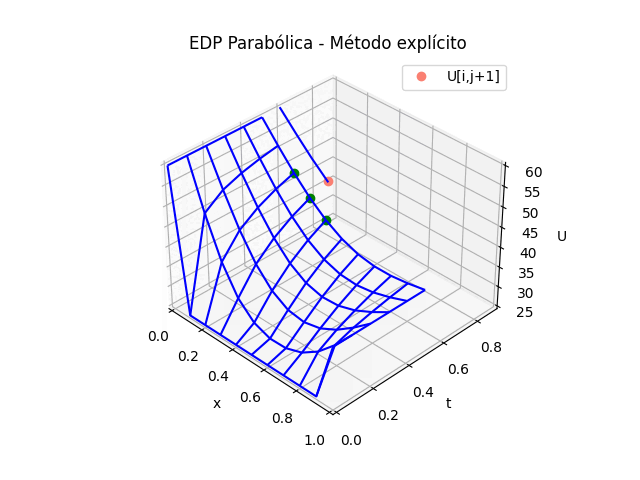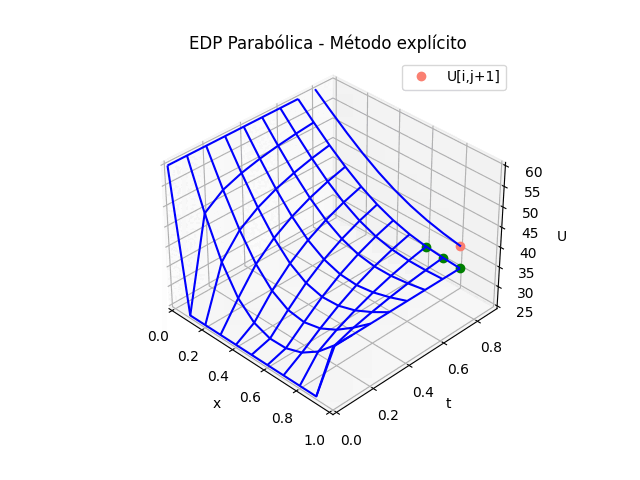
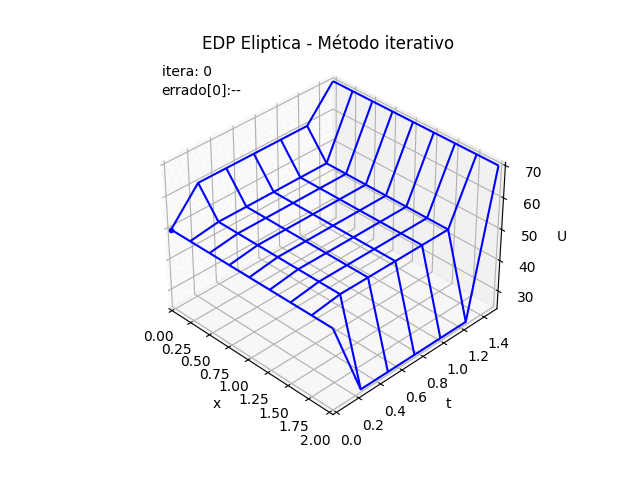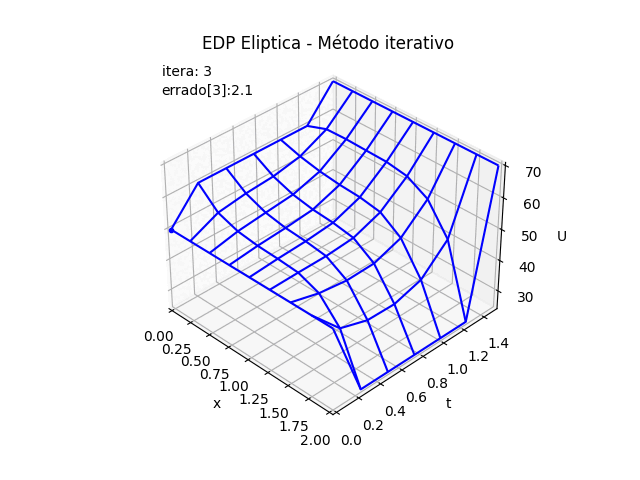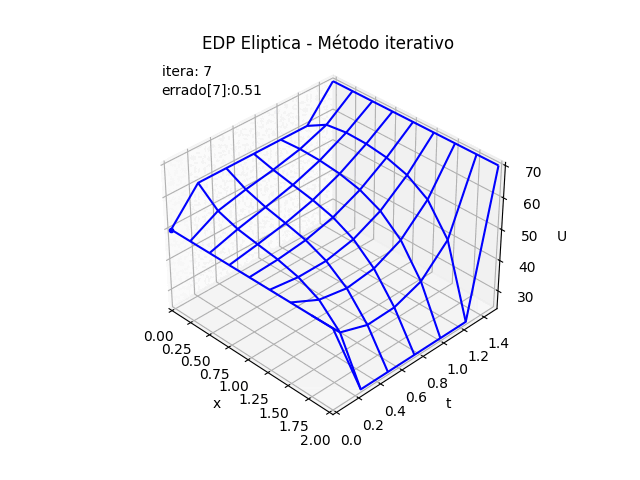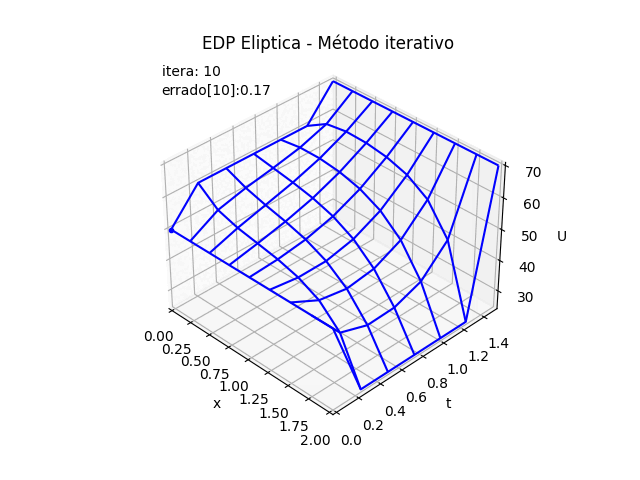
EDP Elípticas [ contínua a discreta ] || Sympy [ iterativo ] [ implícito ] [ gráfica_3D ]
..
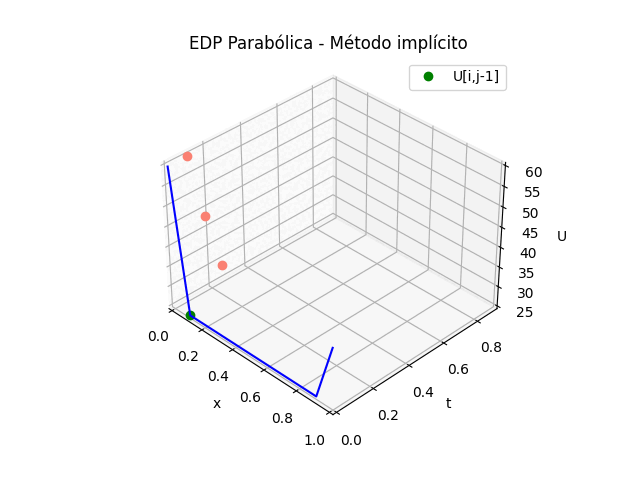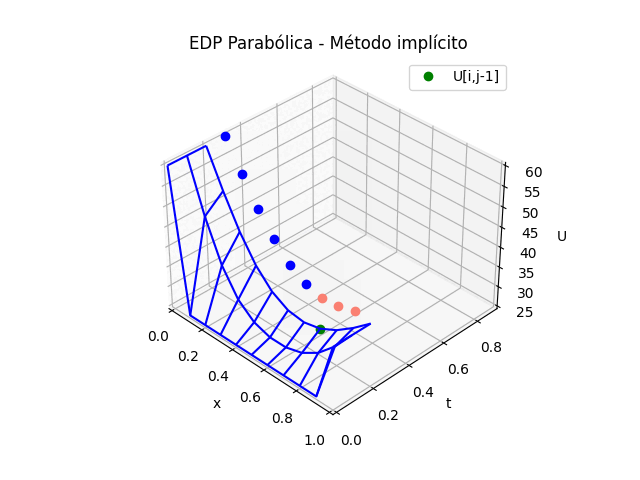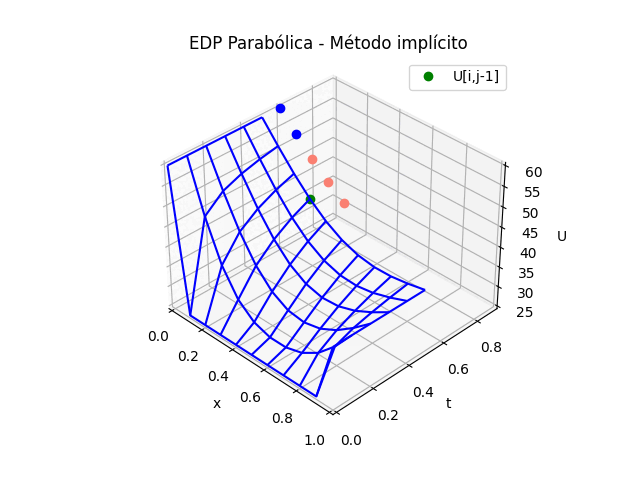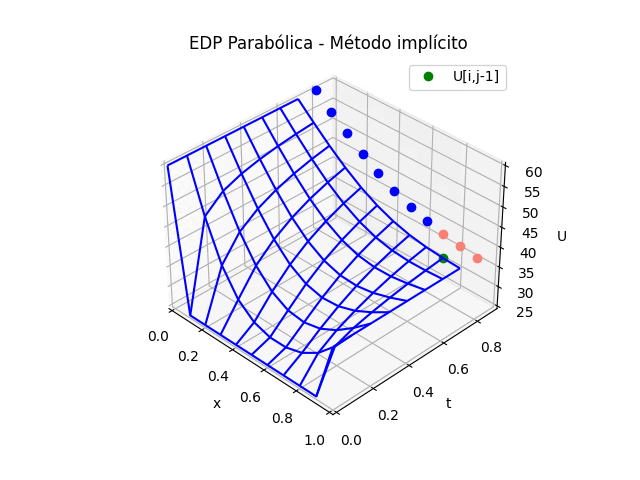
4. EDP Elípticas - Método Implícito con Sympy-Python
Desarrollo analítico del método implicito para una ecuación diferencial parcial elíptica usando Sympy. El algoritmo reutiliza el algoritmo para la EDP Elíptica de contínua a discreta, la creación de la matriz de valores u_xy, y la función
edp_sustituyeValorU() para buscar los valores conocidos de la u(x,y).
El algoritmo usa la ecuación discreta para en cada iteración i,j reemplazar los valores de U conocidos. Los valores de U se escriben en una matriz u_xy, para diferenciar si el valor existe se usa la matriz de estados u_mask.
Con las ecuaciones de cada iteración se llena la matriz A de coeficientes y el vector B de las constantes. Al resolver el sistema de ecuaciones se obtienen todos los valores de la matriz U, completando el ejercicio. Se desarrola la solución al sistema de ecuaciones usando Sympy como alternativa a usar numpy con np.linalg.solve(A.B) que se encuentra como comentario entre las instrucciones.
discreta :
-4⋅U(i, j) + U(i, j - 1) + U(i, j + 1) + U(i - 1, j) + U(i + 1, j) = 0
Método Implícito - EDP Elíptica
j: 1 ; i: 1 ; ecuacion: 0
U(0, 1) + U(1, 0) - 4⋅U(1, 1) + U(1, 2) + U(2, 1) = 0
-4⋅U(1, 1) + U(1, 2) + U(2, 1) = -110.0
j: 1 ; i: 2 ; ecuacion: 1
U(1, 1) + U(2, 0) - 4⋅U(2, 1) + U(2, 2) + U(3, 1) = 0
U(1, 1) - 4⋅U(2, 1) + U(2, 2) + U(3, 1) = -50.0
j: 1 ; i: 3 ; ecuacion: 2
U(2, 1) + U(3, 0) - 4⋅U(3, 1) + U(3, 2) + U(4, 1) = 0
U(2, 1) - 4⋅U(3, 1) + U(3, 2) + U(4, 1) = -50.0
j: 1 ; i: 4 ; ecuacion: 3
U(3, 1) + U(4, 0) - 4⋅U(4, 1) + U(4, 2) + U(5, 1) = 0
U(3, 1) - 4⋅U(4, 1) + U(4, 2) + U(5, 1) = -50.0
j: 1 ; i: 5 ; ecuacion: 4
U(4, 1) + U(5, 0) - 4⋅U(5, 1) + U(5, 2) + U(6, 1) = 0
U(4, 1) - 4⋅U(5, 1) + U(5, 2) + U(6, 1) = -50.0
j: 1 ; i: 6 ; ecuacion: 5
U(5, 1) + U(6, 0) - 4⋅U(6, 1) + U(6, 2) + U(7, 1) = 0
U(5, 1) - 4⋅U(6, 1) + U(6, 2) + U(7, 1) = -50.0
j: 1 ; i: 7 ; ecuacion: 6
U(6, 1) + U(7, 0) - 4⋅U(7, 1) + U(7, 2) + U(8, 1) = 0
U(6, 1) - 4⋅U(7, 1) + U(7, 2) = -75.0
j: 2 ; i: 1 ; ecuacion: 7
U(0, 2) + U(1, 1) - 4⋅U(1, 2) + U(1, 3) + U(2, 2) = 0
U(1, 1) - 4⋅U(1, 2) + U(1, 3) + U(2, 2) = -60.0
j: 2 ; i: 2 ; ecuacion: 8
U(1, 2) + U(2, 1) - 4⋅U(2, 2) + U(2, 3) + U(3, 2) = 0
j: 2 ; i: 3 ; ecuacion: 9
U(2, 2) + U(3, 1) - 4⋅U(3, 2) + U(3, 3) + U(4, 2) = 0
j: 2 ; i: 4 ; ecuacion: 10
U(3, 2) + U(4, 1) - 4⋅U(4, 2) + U(4, 3) + U(5, 2) = 0
j: 2 ; i: 5 ; ecuacion: 11
U(4, 2) + U(5, 1) - 4⋅U(5, 2) + U(5, 3) + U(6, 2) = 0
j: 2 ; i: 6 ; ecuacion: 12
U(5, 2) + U(6, 1) - 4⋅U(6, 2) + U(6, 3) + U(7, 2) = 0
j: 2 ; i: 7 ; ecuacion: 13
U(6, 2) + U(7, 1) - 4⋅U(7, 2) + U(7, 3) + U(8, 2) = 0
U(6, 2) + U(7, 1) - 4⋅U(7, 2) + U(7, 3) = -25.0
j: 3 ; i: 1 ; ecuacion: 14
U(0, 3) + U(1, 2) - 4⋅U(1, 3) + U(1, 4) + U(2, 3) = 0
U(1, 2) - 4⋅U(1, 3) + U(1, 4) + U(2, 3) = -60.0
j: 3 ; i: 2 ; ecuacion: 15
U(1, 3) + U(2, 2) - 4⋅U(2, 3) + U(2, 4) + U(3, 3) = 0
j: 3 ; i: 3 ; ecuacion: 16
U(2, 3) + U(3, 2) - 4⋅U(3, 3) + U(3, 4) + U(4, 3) = 0
j: 3 ; i: 4 ; ecuacion: 17
U(3, 3) + U(4, 2) - 4⋅U(4, 3) + U(4, 4) + U(5, 3) = 0
j: 3 ; i: 5 ; ecuacion: 18
U(4, 3) + U(5, 2) - 4⋅U(5, 3) + U(5, 4) + U(6, 3) = 0
j: 3 ; i: 6 ; ecuacion: 19
U(5, 3) + U(6, 2) - 4⋅U(6, 3) + U(6, 4) + U(7, 3) = 0
j: 3 ; i: 7 ; ecuacion: 20
U(6, 3) + U(7, 2) - 4⋅U(7, 3) + U(7, 4) + U(8, 3) = 0
U(6, 3) + U(7, 2) - 4⋅U(7, 3) + U(7, 4) = -25.0
j: 4 ; i: 1 ; ecuacion: 21
U(0, 4) + U(1, 3) - 4⋅U(1, 4) + U(1, 5) + U(2, 4) = 0
U(1, 3) - 4⋅U(1, 4) + U(1, 5) + U(2, 4) = -60.0
j: 4 ; i: 2 ; ecuacion: 22
U(1, 4) + U(2, 3) - 4⋅U(2, 4) + U(2, 5) + U(3, 4) = 0
j: 4 ; i: 3 ; ecuacion: 23
U(2, 4) + U(3, 3) - 4⋅U(3, 4) + U(3, 5) + U(4, 4) = 0
j: 4 ; i: 4 ; ecuacion: 24
U(3, 4) + U(4, 3) - 4⋅U(4, 4) + U(4, 5) + U(5, 4) = 0
j: 4 ; i: 5 ; ecuacion: 25
U(4, 4) + U(5, 3) - 4⋅U(5, 4) + U(5, 5) + U(6, 4) = 0
j: 4 ; i: 6 ; ecuacion: 26
U(5, 4) + U(6, 3) - 4⋅U(6, 4) + U(6, 5) + U(7, 4) = 0
j: 4 ; i: 7 ; ecuacion: 27
U(6, 4) + U(7, 3) - 4⋅U(7, 4) + U(7, 5) + U(8, 4) = 0
U(6, 4) + U(7, 3) - 4⋅U(7, 4) + U(7, 5) = -25.0
j: 5 ; i: 1 ; ecuacion: 28
U(0, 5) + U(1, 4) - 4⋅U(1, 5) + U(1, 6) + U(2, 5) = 0
U(1, 4) - 4⋅U(1, 5) + U(2, 5) = -130.0
j: 5 ; i: 2 ; ecuacion: 29
U(1, 5) + U(2, 4) - 4⋅U(2, 5) + U(2, 6) + U(3, 5) = 0
U(1, 5) + U(2, 4) - 4⋅U(2, 5) + U(3, 5) = -70.0
j: 5 ; i: 3 ; ecuacion: 30
U(2, 5) + U(3, 4) - 4⋅U(3, 5) + U(3, 6) + U(4, 5) = 0
U(2, 5) + U(3, 4) - 4⋅U(3, 5) + U(4, 5) = -70.0
j: 5 ; i: 4 ; ecuacion: 31
U(3, 5) + U(4, 4) - 4⋅U(4, 5) + U(4, 6) + U(5, 5) = 0
U(3, 5) + U(4, 4) - 4⋅U(4, 5) + U(5, 5) = -70.0
j: 5 ; i: 5 ; ecuacion: 32
U(4, 5) + U(5, 4) - 4⋅U(5, 5) + U(5, 6) + U(6, 5) = 0
U(4, 5) + U(5, 4) - 4⋅U(5, 5) + U(6, 5) = -70.0
j: 5 ; i: 6 ; ecuacion: 33
U(5, 5) + U(6, 4) - 4⋅U(6, 5) + U(6, 6) + U(7, 5) = 0
U(5, 5) + U(6, 4) - 4⋅U(6, 5) + U(7, 5) = -70.0
j: 5 ; i: 7 ; ecuacion: 34
U(6, 5) + U(7, 4) - 4⋅U(7, 5) + U(7, 6) + U(8, 5) = 0
U(6, 5) + U(7, 4) - 4⋅U(7, 5) = -95.0
A :
[[-4. 1. 0. ... 0. 0. 0.]
[ 1. -4. 1. ... 0. 0. 0.]
[ 0. 1. -4. ... 0. 0. 0.]
...
[ 0. 0. 0. ... -4. 1. 0.]
[ 0. 0. 0. ... 1. -4. 1.]
[ 0. 0. 0. ... 0. 1. -4.]]
B :
[-110. -50. -50. -50. -50. -50. -75. -60. 0. 0. 0. 0.
0. -25. -60. 0. 0. 0. 0. 0. -25. -60. 0. 0.
0. 0. 0. -25. -130. -70. -70. -70. -70. -70. -95.]
Resultados para U(x,y)
xi: [0. 0.25 0.5 0.75 1. 1.25 1.5 1.75 2. ]
yj: [0. 0.25 0.5 0.75 1. 1.25 1.5 ]
j, U[i,j]
6 [70. 70. 70. 70. 70. 70. 70. 70. 70.]
5 [60. 64.02 64.97 64.71 63.62 61.44 57.16 47.96 25. ]
4 [60. 61.1 61.14 60.25 58.35 54.98 49.23 39.67 25. ]
3 [60. 59.23 58.25 56.81 54.53 50.89 45.13 36.48 25. ]
2 [60. 57.56 55.82 54.19 52.09 48.92 43.91 36.14 25. ]
1 [60. 55.21 53.27 52.05 50.73 48.78 45.46 39.15 25. ]
0 [50. 50. 50. 50. 50. 50. 50. 50. 50.]
Instrucciones en Python
Las instrucciones completas con Sympy-Python son:
# Ecuaciones Diferenciales Parciales Elipticas
# EDP Elípticas contínua a discreta con Sympy
import numpy as np
import sympy as sym
# u(x,y) funciones continuas y variables simbólicas usadas
x = sym.Symbol('x',real=True)
y = sym.Symbol('y',real=True)
u = sym.Function('u')(x,y) # funcion
f = sym.Function('f')(x,y) # funcion complemento
# U[i,j] funciones discretas y variables simbólicas usadas
i = sym.Symbol('i',integer=True,positive=True)
j = sym.Symbol('j',integer=True,positive=True)
Dx = sym.Symbol('Dx',real=True,positive=True)
Dy = sym.Symbol('Dy',real=True,positive=True)
L = sym.Symbol('L',real=True)
U = sym.Function('U')(i,j)
# INGRESO
fxy = 0*x+0*y # f(x,y) = 0 , ecuacion de Poisson
# ecuacion edp : LHS=RHS
LHS = sym.diff(u,x,2) + sym.diff(u,y,2)
RHS = fxy
edp = sym.Eq(LHS-RHS,0)
# centrada, centrada, atras
dif_dividida ={sym.diff(u,x,2): (U.subs(i,i-1)-2*U+U.subs(i,i+1))/(Dx**2),
sym.diff(u,y,2): (U.subs(j,j-1)-2*U+U.subs(j,j+1))/(Dy**2),
sym.diff(u,y,1): (U - U.subs(j,j-1))/Dy}
# Condiciones iniciales en los bordes
fya = lambda y: 60 +0*y # izquierda
fyb = lambda y: 25 +0*y # derecha
fxc = lambda x: 50 +0*x # inferior
fxd = lambda x: 70 +0*x # superior
# dimensiones de la placa
x0 = 0 # longitud en x
xn = 2
y0 = 0 # longitud en y
yn = 1.5
# muestreo en ejes, discreto, supone dx=dy
dx = 0.25 # Tamaño de paso
dy = dx # supone dx=dy
iteramax = 100 # revisa convergencia
tolera = 0.0001
verdigitos = 2 # para mostrar en tabla de resultados
casicero = 1e-15 # para redondeo de términos en ecuacion
# PROCEDIMIENTO
def edp_discreta(edp,dif_dividida,x,y,u):
''' EDP contínua a discreta, usa diferencias divididas
proporcionadas en parámetros, indica las variables x,y
con función u de (x,y)
'''
resultado={}
# expresión todo a la izquierda LHS (Left Hand side)
LHS = edp.lhs
RHS = edp.rhs
if not(edp.rhs==0):
LHS = LHS-RHS
RHS = 0
edp = sym.Eq(LHS,RHS)
# orden de derivada por x, y
edp_x = edp.subs(x,0)
edp_y = edp.subs(y,0)
ordenDx = sym.ode_order(edp_x,u)
ordenDy = sym.ode_order(edp_y,u)
resultado['ordenDx'] = ordenDx # guarda en resultados
resultado['ordenDy'] = ordenDy
# coeficiente derivada orden mayor a 1 (d2u/dx2)
coeff_x = edp_coef_Dx(edp,x,ordenDx)
if not(coeff_x==1):
LHS = LHS/coeff_x
RHS = RHS/coeff_x
edp = sym.Eq(LHS,RHS)
K_ = edp_coef_Dx(edp,y,ordenDy)
if abs(K_)%1<casicero: # si es entero
K_ = int(K_)
resultado['edp=0'] = edp
resultado['K_'] = K_
discreta = edp.lhs # EDP discreta
for derivada in dif_dividida: # reemplaza diferencia dividida
discreta = discreta.subs(derivada,dif_dividida[derivada])
resultado['discreta=0'] = discreta
return (resultado)
def edp_coef_Dx(edp,x,ordenx):
''' Extrae el coeficiente de la derivada Dx de ordenx
edp es la ecuación como lhs=rhs
'''
coeff_x = 1.0 # valor inicial
# separa cada término de suma
term_suma = sym.Add.make_args(edp.lhs)
for term_k in term_suma:
if term_k.is_Mul: # mas de un factor
factor_Mul = sym.Mul.make_args(term_k)
coeff_temp = 1; coeff_usar=False
# separa cada factor de término
for factor_k in factor_Mul:
if not(factor_k.is_Derivative):
coeff_temp = coeff_temp*factor_k
else: # factor con derivada de ordenx
partes = factor_k.args
if partes[1]==(x,ordenx):
coeff_usar = 1
if coeff_usar==True:
coeff_x = coeff_x*coeff_temp
return(coeff_x)
def redondea_coef(ecuacion, precision=6,casicero = 1e-15):
''' redondea coeficientes de términos suma de una ecuacion
ecuación como lhs=rhs
'''
tipo = type(ecuacion)
tipo_eq = False
if tipo == sym.core.relational.Equality:
RHS = ecuacion.rhs
ecuacion = ecuacion.lhs
tipo = type(ecuacion)
tipo_eq = True
if tipo == sym.core.add.Add: # términos suma de ecuacion
term_sum = sym.Add.make_args(ecuacion)
ecuacion = sym.S.Zero # vacia
for term_k in term_sum:
# factor multiplicativo de termino suma
term_mul = sym.Mul.make_args(term_k)
producto = sym.S.One
for factor in term_mul:
if not(factor.has(sym.Symbol)): # es numerico
factor = np.around(float(factor),precision)
if (abs(factor)%1)<casicero: # si es entero
factor = int(factor)
producto = producto*factor
ecuacion = ecuacion + producto
if tipo == sym.core.mul.Mul: # termino único, busca factores
term_mul = sym.Mul.make_args(ecuacion)
producto = sym.S.One
for factor in term_mul:
if not(factor.has(sym.Symbol)): # es numerico
factor = np.around(float(factor),precision)
if (abs(factor)%1)<casicero: # si es entero
factor = int(factor)
producto = producto*factor
ecuacion = producto
if tipo == float: # # solo un numero
if (abs(ecuacion)%1)<casicero:
ecuacion = int(ecuacion)
if tipo_eq==True: # era igualdad, integra lhs=rhs
ecuacion = sym.Eq(ecuacion,RHS)
return(ecuacion)
def edp_simplificaLamba(resultado,dx,dy):
'''simplifica ecuacion con valores de lambda, dx y dy
entregando la edp discreta simplificada
'''
discreta = resultado['discreta=0']
ordenDy = resultado['ordenDy']
ordenDx = resultado['ordenDx']
K_ = resultado['K_']
lamb = (Dy**ordenDy)/(Dx**ordenDx)
if ordenDy==1 and ordenDx==2:
lamb = lamb/K_
resultado['Lambda_L'] = lamb
# valor de Lambda en ecuacion edp
L_k = lamb.subs([(Dx,dx),(Dy,dy)])
if abs(L_k)%1<casicero: # si es entero
L_k = int(L_k)
resultado['Lambda L_k'] = L_k
# simplifica con lambda L
discreta_L = sym.expand(discreta*(Dy**ordenDy),mul=True)
resultado['(discreta=0)*Dy**ordeny'] = discreta_L
discreta_L = edp_sustituye_L(resultado)
discreta_L = discreta_L.subs(lamb,L)
discreta_L = sym.collect(discreta_L,U)
discreta_L = sym.Eq(discreta_L,0)
resultado['discreta_L = 0'] = discreta_L
# sustituye constantes en ecuación a iterar
discreta_L = discreta_L.subs([(Dx,dx),(Dy,dy),(L,L_k)])
discreta_L = redondea_coef(discreta_L)
resultado['discreta'] = discreta_L
return(resultado)
def edp_sustituye_L(resultado):
''' sustituye lambda con Dy**ordeny/Dx**x/K_
por L, al simplificar Lambda
'''
discreta = resultado['(discreta=0)*Dy**ordeny']
ordenDy = resultado['ordenDy']
ordenDx = resultado['ordenDx']
discreta_L = 0
# separa cada término de suma
term_suma = sym.Add.make_args(discreta)
for term_k in term_suma:
# busca partes de L y cambia por valor L
cambiar = 0 # por orden de derivada
if term_k.has(Dx) and term_k.has(Dy):
partes = term_k.args
ordeny=1
ordenx=1
for unaparte in partes:
if unaparte.has(Dy):
if unaparte.is_Pow:
partey = unaparte.args
ordeny = partey[1]
if unaparte.has(Dx):
if unaparte.is_Pow:
partey = unaparte.args
ordenx = partey[1]
if (ordeny<=ordenDy and ordenx<=-ordenDx):
cambiar=1
if cambiar:
term_k = term_k*L/resultado['Lambda_L']
discreta_L = discreta_L + term_k
# simplifica unos con decimal a entero
discreta_L = discreta_L.subs(1.0,1)
return(discreta_L)
def edp_sustituyeValorU(discreta,xi,yj,u_xy,u_mask):
'''Sustituye en edp discreta los valores conocidos de U[i,j]
tomados desde u_xy, marcados con u_mask
u_mask indica si el valor se ha calculado con edp.
'''
LHS = discreta.lhs # lado izquierdo de ecuacion
RHS = discreta.rhs # lado derecho
# sustituye U[i,j] con valores conocidos
A_diagonal = [] # lista de i,j para matriz de coeficientes A
# Separa términos suma
term_suma = sym.Add.make_args(LHS)
for term_k in term_suma:
# busca U[i,j] y cambia por valor uxt[i,j]
cambiar = 0 ; cambiar_valor = 0 ; cambiar_factor = 0
# separa cada factor de término
factor_Mul = sym.Mul.make_args(term_k)
for factor_k in factor_Mul:
# busca U[i,j] en matriz uxt[i,j]
if factor_k.is_Function:
[i_k,j_k] = factor_k.args
if not(np.isnan(u_xy[i_k,j_k])):
cambiar = u_mask[i_k,j_k]
cambiar_factor = factor_k
cambiar_valor = u_xy[i_k,j_k]
else:
A_diagonal.append([i_k,j_k,term_k/factor_k])
# encontró valor U[i,j],term_k va a la derecha de ecuación
if cambiar:
LHS = LHS - term_k
term_ki = term_k.subs(cambiar_factor,cambiar_valor)
RHS = RHS - term_ki
discreta = sym.Eq(LHS,RHS)
B_diagonal = RHS
resultado = [discreta,A_diagonal,B_diagonal]
return (resultado)
# PROCEDIMIENTO
# transforma edp continua a discreta
resultado = edp_discreta(edp,dif_dividida,x,y,u)
resultado = edp_simplificaLamba(resultado,dx,dy)
discreta = resultado['discreta']
# SALIDA
np.set_printoptions(precision=verdigitos)
algun_numero = [int,float,str,'Lambda L_k']
print('EDP Elíptica contínua a discreta')
for entrada in resultado:
tipo = type(resultado[entrada])
if tipo in algun_numero or entrada in algun_numero:
print('',entrada,':',resultado[entrada])
else:
print('\n',entrada,':')
sym.pprint(resultado[entrada])
# ITERAR para cada i,j dentro de U ------------
# x[i] , y[j] valor en posición en cada eje
xi = np.arange(x0,xn+dx/2,dx)
yj = np.arange(y0,yn+dy/2,dy)
n = len(xi)
m = len(yj)
# Matriz U
u_xy = np.zeros(shape=(n,m),dtype = float)
u_xy = u_xy*np.nan # valor inicial dentro de u
# llena u con valores en fronteras
u_xy[0,:] = fya(yj) # izquierda Ta
u_xy[n-1,:] = fyb(yj) # derecha Tb
u_xy[:,0] = fxc(xi) # inferior Tc
u_xy[:,m-1] = fxd(xi) # superior Td
u0 = np.copy(u_xy) # matriz u inicial
# u_mask[i,j] con valores iniciales o calculados:True
u_mask = np.zeros(shape=(n,m),dtype=bool)
u_mask[0,:] = True # izquierda
u_mask[-1,:] = True # derecha
u_mask[:,0] = True # inferior
u_mask[:,-1] = True # superior
# Método implícito para EDP Elíptica
# ITERAR para plantear las ecuaciones en [i,j]
resultado = {}
eq_itera = [] ; tamano = (n-2)*(m-2)
A = np.zeros(shape=(tamano,tamano),dtype=float)
B = np.zeros(tamano,dtype=float)
for j_k in range(1,m-1,1): # no usar valores en bordes
for i_k in range(1,n-1,1):
eq_conteo = (j_k - 1)*(n-2)+(i_k-1)
discreta_ij = discreta.subs({i:i_k,j:j_k,
x:xi[i_k],y:yj[j_k]})
resultado[eq_conteo]= {'j':j_k, 'i':i_k,
'discreta_ij': discreta_ij}
# usa valores de frontera segun u_mask con True
discreta_k = edp_sustituyeValorU(discreta_ij,
xi,yj,u_xy,u_mask)
discreta_ij = discreta_k[0]
A_diagonal = discreta_k[1] # lista de (i,j,coeficiente)
B_diagonal = discreta_k[2]
resultado[eq_conteo]['discreta_k'] = discreta_k[0]
# añade ecuacion a resolver
eq_itera.append(discreta_ij)
# Aplica coeficientes de ecuacion en A y B:
# A_diagonal tiene lista de (i,j,coeficiente)
for uncoeff in A_diagonal:
columna = (uncoeff[1]-1)*(n-2)+(uncoeff[0]-1)
fila = (j_k - 1)*(n-2)+(i_k-1)
A[fila,columna] = uncoeff[2]
B[eq_conteo] = float(B_diagonal) # discreta_ij.rhs
resultado['A'] = np.copy(A)
resultado['B'] = np.copy(B)
# resuelve el sistema de ecuaciones en eq_itera en Sympy
X_k = sym.solve(eq_itera)[0]
# actualiza uxt[i,j] , u_mask segun X_k en Sympy
for nodo_Uij in X_k:
[i_k,j_k] = nodo_Uij.args
u_xy[i_k,j_k] = X_k[nodo_Uij]
u_mask[i_k,j_k] = True
# resuelve el sistema A.X=B en Numpy
#X = np.linalg.solve(A,B)
# tarea: llevar valores X a u_xy
# SALIDA
np.set_printoptions(precision=verdigitos)
algun_numero = [int,float,str,'Lambda L_k']
print('\nMétodo Implícito - EDP Elíptica')
for entrada in resultado:
tipo = type(resultado[entrada])
if tipo in algun_numero or entrada in algun_numero:
print('',entrada,':',resultado[entrada])
elif (tipo==dict):
print('j:',resultado[entrada]['j'],'; '
'i:',resultado[entrada]['i'],'; '
'ecuacion:',entrada)
sym.pprint(resultado[entrada]['discreta_ij'])
if resultado[entrada]['discreta_k'].rhs!=0:
sym.pprint(resultado[entrada]['discreta_k'])
else:
print('\n',entrada,': \n',resultado[entrada])
print('Resultados para U(x,y)')
print('xi:',xi)
print('yj:',yj)
print(' j, U[i,j]')
for j_k in range(m-1,-1,-1):
print(j_k, (u_xy[:,j_k]))
EDP Elípticas [ contínua a discreta ] || Sympy [ iterativo ] [ implícito ] [ gráfica_3D ]
 En el caso de entradas a puertos comerciales de alto tráfico y limitado espacio se convierten el una herramienta indispensable para gestionar las recorridos de ingreso o salida.
En el caso de entradas a puertos comerciales de alto tráfico y limitado espacio se convierten el una herramienta indispensable para gestionar las recorridos de ingreso o salida.