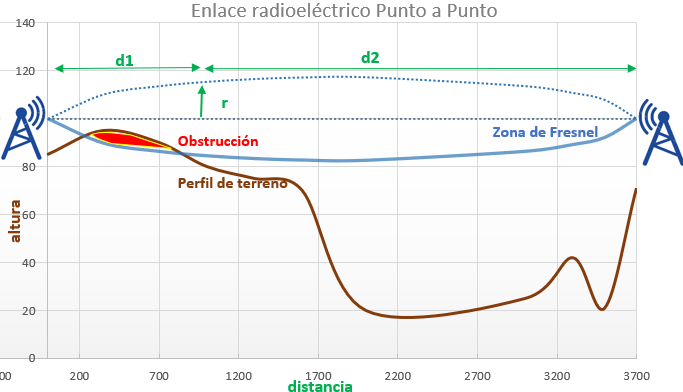
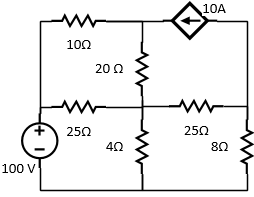
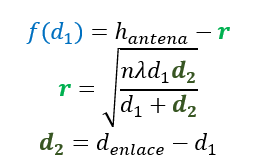Algoritmos101

Cursos Python

Categoría: 1ra Evaluación

  • 1Eva_2022PAOI_T1 Impacto en trayectoria del drone

    1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

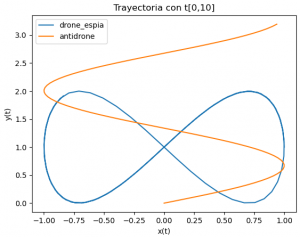
    Tema 1 (30 puntos) La trayectoria automática de un drone espía en un territorio de guerra esta descrita por x1(t), y1(t).
    trayectoria drone parametricaDrone
    x1(t) = cos(t)
    y1(t) = sin(2 t)

    Antidrone
    x2(t) = sin(0.75 t)
    y2(t) = k t

    Durante un intervalo de tiempo t entre [0,10] segundos, se dispara un misil antidrone con trayectoria descrita por x2(t), y2(t). El antidrone tiene un parámetro de control constante denominado k para y2(t) que se establece antes del disparo.

    Encuentre el valor de k que produce el impacto que destruye el Drone.

    Para que se produzca el impacto, deben coincidir las coordenadas x,y para ambas trayectorias, al mismo valor de tiempo.
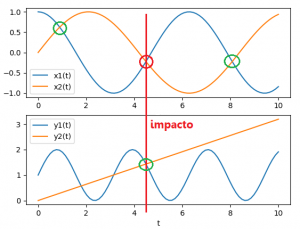
    trayectoria drone vs tiempo
    a) Realice el planteamiento del problema usando inicialmente las trayectorias en el eje x, donde para el intervalo de operación del misil antidrone, se observa más de un impacto.

    b) Usando el método de Newton-Raphson encuentre el valor de t en el cual se pretende realizar el impacto al drone. Realice al menos 3 iteraciones de forma analítica, use tolerancia de 10-4,

    c) Realice el análisis de la convergencia del método.

    d) Con el resultado de t anterior, determine el valor de la constante k para la expresión de y2(t) que asegura el impacto contra el drone.

    Rúbrica: literal a (5 puntos), iteraciones (9 puntos), errores entre iteraciones(6 puntos), análisis de convergencia(5 puntos), literal d(5 puntos)

    Referencia: Domo de Hierro, así funciona el escudo antimisiles de Israel. CNN en español. 15-mayo-2021.

    Lo que hay que saber sobre los misiles hipersónicos disparados por Rusia contra Ucrania. cnnespanol.cnn.com 10-mayo-2022. https://cnnespanol.cnn.com/2022/05/10/misiles-hipersonicos-rusia-ucrania-trax/

  • 1Eva_2021PAOII_T3 Nutrientes en asociación de cultivos

    1ra Evaluación 2021-2022 PAO II. 24/Noviembre/2021

    Tema 3. (40 puntos) La asociación de cultivos es la siembra de dos o más especies vegetales muy próximas entre sí, de tal manera que una o ambas pueden obtener tales como la mejora de la productividad, control de plagas, la prevención de enfermedades o adquirir un mejor sabor.

    nutrientes en asociación de cultivosLos beneficios se obtienen a través de la absorción de nutrientes o de cambios en el medio ambiente.

    Una forma de medir la absorción de un nutriente de cada especie por ciclo de cultivo es cambiar la cantidad de especies vegetales en distintas parcelas. La diferencia de un nutriente entre el fin e inicio del cultivo se encuentra mostrada en la siguiente tabla.

    plátano café cacao Absorción de nutriente
    40 110 310 750
    400 15 25 445
    200 560 310 10

    a. Realice el planteamiento del sistema de ecuaciones, presente en la forma Ax=B.

    b. De ser necesario, realice operaciones con la matriz aumentada para mejorar la convergencia con un método iterativo.

    c. En el contexto del problema, proponga un vector inicial y tolerancia.

    d. Realice 3 iteraciones con el método de Gauss-Seidel y estime el error (papel y lápiz)

    e. Describa y justifique su observación sobre la convergencia del método y estime una descripción de los resultados.

    Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), iteraciones (15 puntos) cálculo de error(5 puntos), literal d(5 puntos)

    Referencia: Asociación de cultivos https://huertocity.com/index.php/asociacion-de-cultivos/
    Tabla Asociación de cultivos: 12 ejemplos, importancia. https://ingenieriaambiental.net/asociacion-de-cultivos/

     

  • 1Eva_2021PAOII_T2 Intersección de funciones - Obstrucción Radioenlace

    1ra Evaluación 2021-2022 PAO II. 24/Noviembre/2021

    Tema 2. (30 puntos) En un enlace radioeléctrico, se denomina “Zona de Fresnel” al espacio entre un emisor y receptor debe estar libre para minimizar atenuaciones a la onda de propagación.

    Una obstrucción es una parte del perfil del terreno que se encuentra dentro de la Zona de Fresnel. El perfil del terreno es la expresión del polinomio del tema anterior P3(d1) en el intervalo [0,1300].

    Cuando las antenas del transmisor y receptor se encuentran a la misma altura, la parte inferior del lóbulo, f(d1), se determina a partir de las siguientes fórmulas:

    formulas de enlace zona fresnelConsidere los valores de las constantes hantena= 100 m, n =1, λ=0.3278, denlace=3700 m

    Para analizar la obstrucción, se debe determinar los puntos de intersección entre P3(d1) y f(d1)

    a. Establezca un intervalo de análisis para cada raíz.

    b. Realice al menos 3 iteraciones con el método de la Bisección para encontrar la primera raíz (izquierda)

    c. Desarrolle al menos 3 iteraciones con el método del Punto fijo para encontrar el segundo punto (derecha)

    d. Realice al menos 3 iteraciones con el método de Newton-Raphson para determinar la altura del perfil que genera el mayor obstáculo dentro del intervalo (altura máxima).

    Rúbrica: literal a (4 puntos), literal b (10 puntos), literal c (10 puntos), literal d (6 puntos)

    Referencia: Zona de Fresnel, https://youtu.be/v371pPLdf_c

  • 1Eva_2021PAOII_T1 Interpolación para perfil de terreno

    1ra Evaluación 2021-2022 PAO II. 24/Noviembre/2021

    Tema 1. (30 puntos) Para el diseño de los enlaces radioeléctricos “punto a punto” se analiza “Zona de Fresnel” que para una buena propagación de señal debe estar libre de obstrucciones.

    La altura o perfil del terreno muestra la sección que produce atenuación en la señal del enlace.

    Enlace Zona Fresnel 01

    La tabla muestra el perfil para un enlace donde se requiere analizar el intervalo entre 0 y 1300 metros desde la antena ubicada en el extremo izquierdo.

    distancia d1 0 350 700 1000 1300 1600 2000 3000 3300 3500 3700
    Perfil de Terreno 85 95 90 80 75 70 20 25 42 21 71

    a. Plantee y desarrolle un polinomio P3(d1) de grado 3, que describa el perfil del terreno en el intervalo [0,1300] de distancias a la primera antena d1.
    b. Calcule el error sobre el o los datos que no se usaron en el intervalo
    c. Desarrolle y justifique una propuesta para disminuir los errores encontrados en el literal anterior, sobre el mismo intervalo, es decir obtiene un nuevo polinomio (use algoritmo).
    d. Escriba sus conclusiones y recomendaciones sobre los resultados obtenidos entre los dos polinomios.

    Rúbrica: literal a (10 puntos), literal b (4 puntos), literal c (10 puntos), literal d (6 puntos)

    Referencia: Zona de Fresnel. https://es.wikipedia.org/wiki/Zona_de_Fresnel

  • 1Eva_2021PAOI_T1 Función recursiva y raíces de ecuaciones

    1ra Evaluación 2021-2022 PAO I. 6/Julio/2021

    Tema 1. (30 puntos) La sucesión mostrada puede ser calculada de forma recursiva para un valor inicial x0.

    x_n = ln \Bigg(\frac{1}{2+x_{n-1}} \Bigg)

    n = 1, 2, 3, ...
    x0 = -0.45

    a. Realice 7 iteraciones con la sucesión, tabule y grafique los resultados.

    Considerando solamente el intervalo  [-0.5,-0.4]

    b. ¿Se puede afirmar que para todo valor inicial x0 la sucesión converge? Justifique su respuesta.

    En algoritmos de computadora, la forma recursiva de la sucesión puede consumir rápidamente recursos, por lo que se plantea encontrar el valor al que converge la sucesión usando siguiente ecuación:

    x +ln(x+2) = 0

    x0 = -0.45

    c. Encuentre el valor que resuelve la ecuación usando el método de Newton-Raphson con tolerancia de 10-4. Realice al menos 3 iteraciones completas y comente sobre la convergencia.

    d. Presente sus conclusiones y recomendaciones para los resultados obtenidos entre el literal b y c.

    Rúbrica: literal a (5 puntos), literal b (3 puntos), literal c, verifica intervalo (4 puntos), iteraciones (10 puntos), convergencia (5 puntos), literal d (4 puntos)

     

  • 1Eva_2021PAOI_T3 Interpolar, modelo de contagios 2020

    1ra Evaluación 2021-2022 PAO I. 6/Julio/2021

    Tema 3 (35 puntos) Para evaluar las medidas de confinamiento aplicadas durante el año 2020 se requiere de un modelo del comportamiento de contagios por unidad de tiempo.

    Se disponen de los datos de casos graves por semana mostrados en la tabla y se busca obtener un polinomio de interpolación de grado 4 semejante al mostrado en la figura.

    1Eva2021PAOI Confinamiento 2020

    Semana Fecha casos graves
    … … …
    9 2/3/2020 1435
    10 9/3/2020 1645
    11 16/3/2020 1503
    12 23/3/2020 3728
    13 30/3/2020 7154
    14 6/4/2020 6344
    15 13/4/2020 4417
    16 20/4/2020 3439
    17 27/4/2020 2791
    18 4/5/2020 2576
    19 11/5/2020 2290
    20 18/5/2020 2123
    21 25/5/2020 2023
    22 1/6/2020 2067
    23 8/6/2020 2163
    24 15/6/2020 2120
    25 22/6/2020 2125
    … … …

    a. Desarrolle el polinomio de interpolación usando los puntos sombreados en la tabla, correspondientes a las semanas 11, 13, 16, 18 y 20.

    b. Calcule los errores en el intervalo sobre los datos que no se usaron entre las semanas [11,20]

    c. Desarrolle y justifique una propuesta para disminuir los errores encontrados en el literal anterior, sobre el mismo intervalo, es decir obtiene un nuevo polinomio.

    d. Calcule los errores en el intervalo para el modelo del literal c y compare con los obtenidos en el literal b.

    e. Escriba sus conclusiones y recomendaciones sobre los resultados obtenidos entre los dos polinomios.

    Rúbrica: literal a (7 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (8 puntos)

    xi = [    9,   10,   11,   12,   13,   14,
         15,   16,   17,   18,   19,   20,
         21,   22,   23,   24,   25,   26 ]
fi = [ 1435, 1645, 1503, 3728, 7154, 6344,
       4417, 3439, 2791, 2576, 2290, 2123,
       2023, 2067, 2163, 2120, 2125, 2224 ]

    Referencia:
    - Eluniverso.com. 2/07/2021. Casos de coronavirus en Ecuador al viernes 2 de julio: 461.157 confirmados, 21.623 fallecidos y 1′416.916 vacunados. https://www.eluniverso.com/noticias/ecuador/coronavirus-covid-19-ecuador-cifras-vacunados-casos-contagios-muertes-9-junio-2021-nota-18/ .

    - https://flo.uri.sh/visualisation/5585865/embed

    - BBC News Mundo. La “doble curva” del coronavirus y el “falso dilema” entre salvar vidas o la economía. 8/mayo/2020. https://youtu.be/SlTSFkTsZL8

  • 1Eva_2021PAOI_T2 Atención hospitalaria con medicamentos limitados

    1ra Evaluación 2021-2022 PAO I. 6/Julio/2021

    Tema 2 (35 puntos) Durante el año 2020, ante el aumento de atención hospitalaria estatal en la región y el limitado acceso a medicamentos, como una primera estrategia de manejo de recursos se derivan el exceso de pacientes hacia la atención en hospitales privados. hospital dibujo con ambulancia

    En la tabla  se muestra la cantidad de los tres medicamentos (mg, ml) que se administran al atender a cada paciente clasificado por grupo etario: niños, adolescentes, adultos y adultos mayores.

    También se dispone del total de medicamentos existente en bodegas en cada semana.

    Niños Adolescentes Adultos Adultos Mayores Medicamentos /semana
    Medicamento_A 0.3 0.4 1.1 4.7 3500
    Medicamento_B 1 3.9 0.15 0.25 3450
    Medicamento_C 0 2.1 5.6 1.0 6500

    Es de interés conocer la cantidad de pacientes de cada grupo que se podría atender con los recursos disponibles.

    a.  Realice el planteamiento de un sistema de ecuaciones que permita determinar la cantidad máxima de pacientes de cada grupo etario que podrían ser atendidos usando todos los medicamentos disponibles.

    Una vez planteadas las ecuaciones, se le indica que la capacidad K para pacientes niños sea una variable libre, por consumir menos recursos y se podrían derivar al sistema privado.

    b.  Escriba el conjunto de soluciones posibles en función de la variable libre, considerando la cantidad de niños a atender como máximo de K=100.

    c. Determine la capacidad de atención usando un método Iterativo con una tolerancia de 10-2. Realice tres iteraciones completas y revise la convergencia del método. Se estima atender al inicio de semana al menos 100 pacientes de cada grupo.

    d. Suponga que la cantidad de pacientes en cada grupo para una semana dada es: [350, 1400, 1500, 1040]. ¿Hay suficiente cantidad de medicamentos para atender el promedio actual de pacientes? Analice y describa los resultados encontrados.

    e. Si se decide vacunar primero a todos los niños, entonces ya no requieren atención hospitalaria (K=0) ¿Cuál es el número máximo de pacientes de cada grupo que podría incrementarse dadas las condiciones actuales? Resuelva usando un método directo.

    Rúbrica: literal a (3 puntos), literal b (2 puntos), pivoteo por filas(5 puntos), iteraciones (10 puntos), análisis de convergencia (4 puntos), literal d (5 puntos) literal e (6 puntos)

    Referencias:
    - BBC News Mundo. El país que está vacunando contra el covid-19 primero a los jóvenes y no a los ancianos. 16/enero/2021. https://youtu.be/oo2itoBBwyY

    - Manejo clínico de la COVID-19, orientaciones provisionales 27/mayo/2020. https://apps.who.int/iris/bitstream/handle/10665/332638/WHO-2019-nCoV-clinical-2020.5-spa.pdf

  • 1Eva_IIT2019_T1 Ecuación Recursiva

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 1. (30 puntos). Considere la sucesión

    \Big( x_n \Big)_{n=0}^{+ \infty}

    cuya ecuación recursiva es:

    x_n = g(x) = \sqrt{3 + x_{n-1}}

    para n  ∈ Ν

    a) ¿Se puede afirmar que ∀x ∈ [1,3], g(x) ∈ [1,3]?

    b) Pruebe que g es una función contractiva en el intervalo [1,3] y estime el valor de la constante de Lipschitz (cota de la derivada de g)

    c) Realice 5 iteraciones partiendo del dato inicial x0 =2, y determine el orden de convergencia.

    d) Encuentre el valor teórico de x* al cual converge la sucesión y estime el error absolito en la iteración 5.

    e) Realice 5 iteraciones con el método de bisección en el intervalo [1,3] para aproximar el punto fijo de la función g(x).

    Rúbrica: literal a (3 puntos), literal b (3 puntos), literal c (10 puntos), literal d (4 puntos), literal e (10 puntos)

    Referencia: Burden 9Ed. Definición 10.5 p633, Theorem 2.4 P62;
    Contracción https://es.wikipedia.org/wiki/Contracci%C3%B3n_(espacio_m%C3%A9trico).
    Función lipschitziana https://es.wikipedia.org/wiki/Funci%C3%B3n_lipschitziana

     

  • 1Eva_IIT2019_T2 Proceso Termodinámico

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 2. (20 puntos).  Para simular la disminución de la temperatura en un proceso termodinámico, mechero calienta una barra
    un algoritmo evolutivo necesita usar un polinomio para aproximar en el intervalo [0,4] la función f con regla de correspondencia

    f(x)=e^{-0.5x}

    con constante k = 0.5

    Para construir el mencionado polinomio, considere la tabla:

    x 0 1 2 3 4
    f(x) f(0) f(1) f(2) f(3) f(4)

    a. Aplique interpolación polinomial y aproxime el valor de f(2.4) usando un polinomio de grado 2.

    b. Encuentre una cota superior para el error de interpolación en la aproximación de f(1.7)}

    Rúbrica: literal a (15 puntos), literal b (5 puntos)

  • 1Eva_IIT2019_T3 Circuito eléctrico

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 3. (30 puntos) El sistema de ecuaciones que sigue se generó por medio de aplicar la ley de malla de corriente al circuito de la figura. circuito eléctrico con resistencias y fuentes

    \begin{cases} 55 I_1 - 25 I_4 = -200 \\ -37 I_3 - 4 I_4 = -250 \\ -25 I_1 - 4 I_3 + 29 I_4 = 100 \end{cases}

    a) Use el método de eliminación de Gauss para calcular I1, I3, I4, I1 observando que
    I2 = -10

    b) Encuentre la norma infinita de la matriz de transición T en el método de Jacobi y comente.

    c) Con el método de Gauss-Seidel realice tres iteraciones comenzando con el vector cero. Además en la tercera iteración, encuentre una cota para el error relativo.

    Rúbrica: literal a (12 puntos), literal b (6 puntos), literal c (12 puntos)

    A = [[ 55.0, 0,  0, -25],
     [  0  , 0,-37,  -4],
     [-25  , 0, -4,  29],
     [  0  ,  1, 0,   0]]

B = [-200,-250,100,-10]