Ejercicio: 1Eva_IT2017_T2 Tanque esférico-volumen
a. Planteamiento del problema
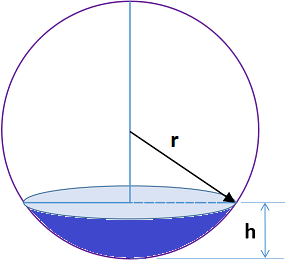
V = \frac{\pi h^{2} (3r-h)}{3}Si r=1 m y V=0.75 m3,
0.75 = \frac{\pi h^{2} (3(1)-h)}{3} 0.75 -\frac{\pi h^{2} (3(1)-h)}{3} = 0 f(h) = 0.75 -\frac{\pi h^{2} (3-h)}{3} = 0.75 -\frac{\pi}{3}(h^{2} (3)-h^{2}h) = 0.75 -\frac{\pi}{3}(3 h^{2} - h^{3}) f(h) = 0.75 -\pi h^{2} + \frac{\pi}{3}h^{3}b. Intervalo de búsqueda de raíz
El tanque vacio tiene h=0 y completamente lleno h= 2r = 2(1) = 2, por lo que el intevalo tiene como extremos:
[0,2]
Verificando que exista cambio de signo en la función:
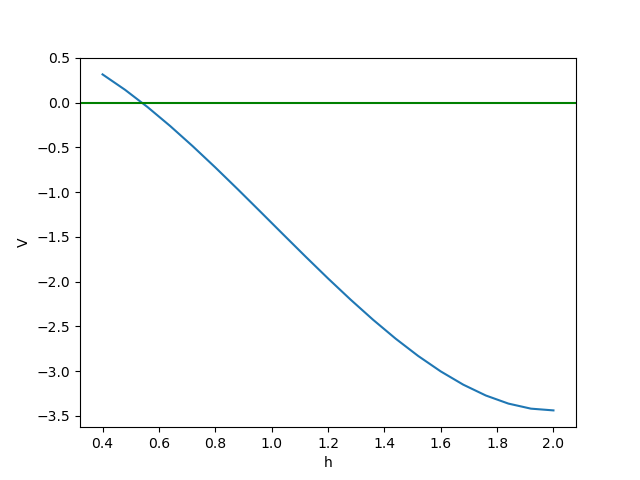
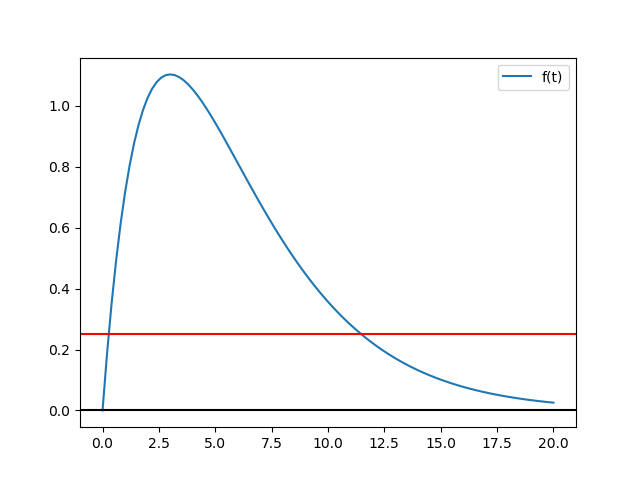
f(0) = 0.75 -\pi (0)^{2} + \frac{\pi}{3}(0)^{3} = 0.75 f(2) = 0.75 -\pi (2)^{2} + \frac{\pi}{3}(2)^{3}= -3.4387y verificando al usar la gráfica dentro del intervalo:
Tolerancia
Se indica en el enunciado como 0.01 que es la medición mínima a observar con un flexómetro.
tolera = 0.01
c. Método de Newton-Raphson
d. Método de Punto Fijo
c. Método de Newton-Raphson
El método de Newton-Raphson requiere la derivada de la función:
x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)} f(h) = 0.75 -\pi h^{2} + \frac{\pi}{3}h^{3} f'(h) = -2\pi h + \pi h^{2}Tomando como punto inicial de búsqueda el extremo izquierdo del intervalo, genera una división para cero. Por lo que se mueve un poco a la derecha, algo más cercano a la raiz, viendo la gráfica por ejemplo 0.1
x0 = 0.1
iteración 1
i =0
f(0.1) = 0.75 -\pi (0.1)^{2} + \frac{\pi}{3}(0.1)^{3} =0.7196 f'(0.1) = -2\pi (0.1) + \pi (0.1)^{2} = -0.5969 x_{1} = x_0 -\frac{0.7496 }{-0.0625} = 1.3056 tramo = |x_{1}-x_{0}| = |0.1-1.3056 | = 1.2056iteración 2
i =1
f(1.3056) = 0.75 -\pi (1.3056)^{2} + \frac{\pi}{3}(1.3056)^{3} = -2.2746 f'(1.3056) = -2\pi (1.3056) + \pi (1.3056)^{2} =-2.8481 x_{1} = x_0 -\frac{-2.2746}{-2.8481} = 0.5069 tramo = |x_{2}-x_{1}|=|0.5069-1.3056|=0.7987iteración 3
i =2
f(0.5069) = 0.75 -\pi (0.5069)^{2} + \frac{\pi}{3}(0.5069)^{3} = 0.0789 f'(0.5069) = -2\pi (0.5069) + \pi (0.5069)^{2} =-2.3780 x_{1} = x_0 -\frac{0.0789}{-2.3780} = 0.5401 tramo = |x_{3}-x_{2}| =|0.5401 - 0.5069| = 0.0332Observe que el tramo disminuye en cada iteración , por lo que el método converge, si se siguen haciendo las operaciones se tiene que:
[ xi, xnuevo, tramo] [[1.00000000e-01 1.30560920e+00 1.20560920e+00] [1.30560920e+00 5.06991599e-01 7.98617601e-01] [5.06991599e-01 5.40192334e-01 3.32007350e-02] [5.40192334e-01 5.39518667e-01 6.73667593e-04]] raiz 0.5395186666699257
Instrucciones en Python
para Método de Newton-Raphson
# 1Eva_IT2017_T2 Tanque esférico-volumen import numpy as np import matplotlib.pyplot as plt # INGRESO fx = lambda h: 0.75 - np.pi*(h**2)+(np.pi/3)*h**3 dfx = lambda h: -2*np.pi*h+np.pi*(h**2) # Parámetros de método a = 0 b = 2 tolera = 0.01 x0 = 0.1 iteramax = 100 # parametros de gráfica La = a Lb = b muestras = 21 # PROCEDIMIENTO # Newton-Raphson tabla = [] tramo = abs(2*tolera) xi = x0 while (tramo>=tolera): xnuevo = xi - fx(xi)/dfx(xi) tramo = abs(xnuevo-xi) tabla.append([xi,xnuevo,tramo]) xi = xnuevo tabla = np.array(tabla) # calcula para grafica hi = np.linspace(La,Lb,muestras) fi = fx(hi) gi = dfx(hi) # SALIDA print(' [ xi, xnuevo, tramo]') print(tabla) print('raiz', xnuevo) plt.plot(hi,fi) plt.plot(xi,fx(xi),'ro') plt.axhline(0, color='green') plt.xlabel('h') plt.ylabel('V') plt.title('Método Newton-Raphson') plt.show()
d. Método de Punto Fijo
Del planteamiento del problema en el literal a, se tiene que:
0.75 = \frac{\pi h^{2} (3(1)-h)}{3}de donde se despeja una h:
\frac{3(0.75)}{\pi (3(1)-h) } = h^{2} h = \sqrt{\frac{3*0.75}{\pi (3-h) }} h = \sqrt{\frac{2.25}{\pi (3-h) }}con lo que se obtienen las expresiones a usar en el método
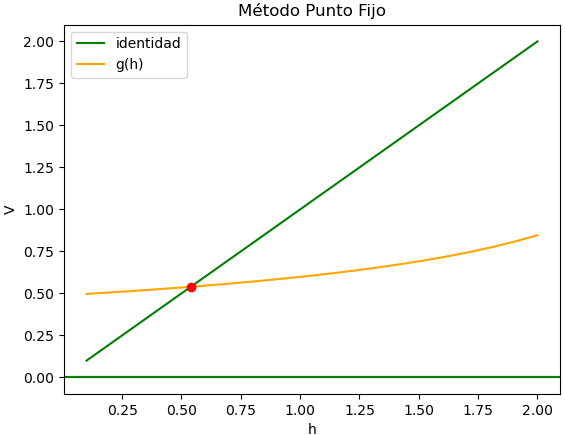
identidad = h g(h) = \sqrt{\frac{2.25}{\pi (3-h) }}El punto inicial de búsqueda debe encontrarse en el intervalo, se toma el mismo valor que x0 en el método de Newton-Raphson
x0 = 0.10
Iteracion 1
x_0= 0.10 g(0.10) = \sqrt{\frac{2.25}{\pi (3-(0.10) }}= 0.4969 tramo= |0.4969-0.10| = 0.3869Iteracion 2
Iteracion 3
con lo que se cumple el criterio de tolerancia, y se obtiene la raiz de:
raiz = 0.5390
Tabla de resultados, donde se observa que el tramo o error en cada iteración disminuye, por lo que el método converge.
[i,xi,xi+1,tramo] [[1. 0.1 0.4969553 0.3969553 ] [2. 0.4969553 0.5349116 0.03795631] [3. 0.5349116 0.53901404 0.00410243]] raiz 0.5390140355891347 >>>
Instrucciones en Python
para Método de Punto-Fijo, recordamos que el método puede diverger, por lo que se añade el parámetro iteramax
# 1Eva_IT2017_T2 Tanque esférico-volumen import numpy as np import matplotlib.pyplot as plt # INGRESO fx = lambda h: h gx = lambda h: np.sqrt(2.25/(np.pi*(3-h))) a = 0.1 b = 2 tolera = 0.01 iteramax = 100 La = a Lb = b muestras = 21 # PROCEDIMIENTO # Punto Fijo tabla = [] i = 1 # iteración b = gx(a) tramo = abs(b-a) while not(tramo<=tolera or i>=iteramax): tabla.append([i,a,b,tramo]) a = b b = gx(a) tramo = abs(b-a) i = i+1 tabla.append([i,a,b,tramo]) respuesta = b # Validar respuesta if (i>=iteramax): respuesta = np.nan tabla = np.array(tabla) # calcula para grafica hi = np.linspace(La,Lb,muestras) fi = fx(hi) gi = gx(hi) # SALIDA print(' [i, xi, xi+1, tramo]') print(tabla) print('raiz', respuesta) plt.plot(hi,fi, label = 'identidad', color='green') plt.plot(hi,gi, label = 'g(h)', color = 'orange') plt.plot(b,gx(b),'ro') plt.axhline(0, color='green') plt.xlabel('h') plt.ylabel('V') plt.title('Método Punto Fijo') plt.legend() plt.axhline(0, color='green') plt.show()
Otra forma de probar la convergencia es que |g'(x)|<1 que se observa en la una gráfica adicional, lo que limita aún más el intervalo de búsqueda.
Desarrollo en la siguiente clase.