ejercicio: 1Eva_2023PAOI_T3 Recoger los restos de sumergible
literal a
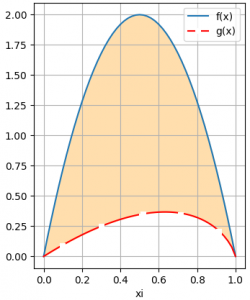
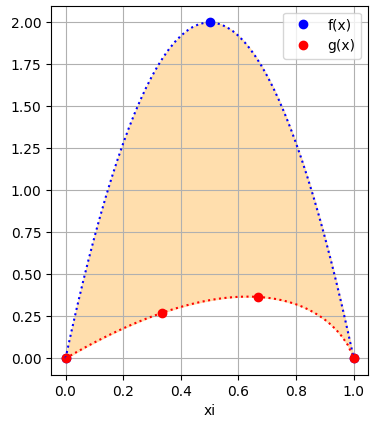
Para realizar el planteamiento del ejercicio, se realiza la gráfica para observar mejor los puntos.
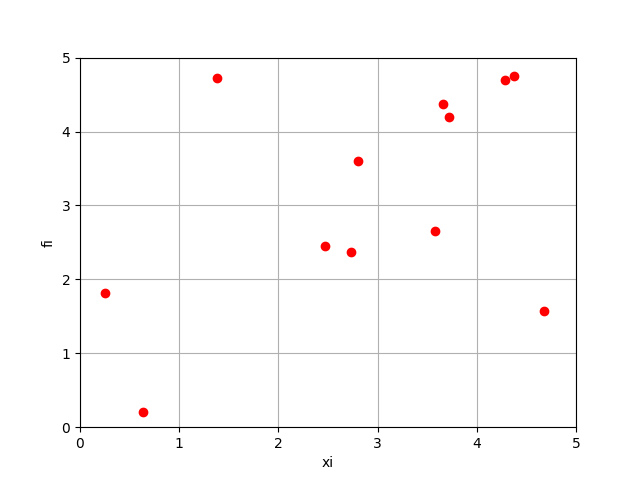
Se podría observar los puntos y plantear un primer recorrido como el siguiente
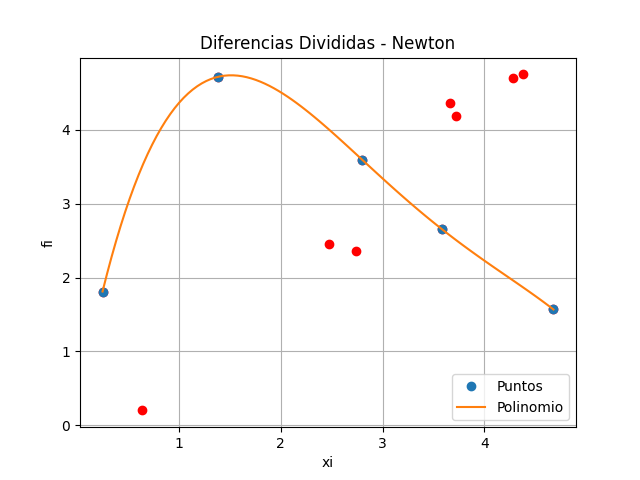
los puntos corresponden a los índices j = [0 ,2, 5, 6, 11]:
# INGRESO
xj = np.array([0.2478, 0.6316, 1.3802, 2.4744, 2.7351, 2.8008,
3.5830, 3.6627, 3.7213, 4.2796, 4.3757, 4.6794])
fj = np.array([1.8108, 0.1993, 4.7199, 2.4529, 2.3644, 3.5955,
2.6558, 4.3657, 4.1932, 4.6998, 4.7536, 1.5673])
# selecionando puntos
j = [0, 2, 5, 6, 11]
xi = xj[j]
fi = fj[j]
literal b
Partiendo del algoritmo de Diferencias divididas de Newton, y añadiendo vectores xj y fj para todos los puntos dados en el ejercicio.
Tabla Diferencia Dividida
[['i ', 'xi ', 'fi ', 'F[1]', 'F[2]', 'F[3]', 'F[4]', 'F[5]']]
[[ 0. 0.2478 1.8108 2.569 -1.3163 0.3389 -0.0561 0. ]
[ 1. 1.3802 4.7199 -0.7915 -0.1861 0.09 0. 0. ]
[ 2. 2.8008 3.5955 -1.2014 0.111 0. 0. 0. ]
[ 3. 3.583 2.6558 -0.9928 0. 0. 0. 0. ]
[ 4. 4.6794 1.5673 0. 0. 0. 0. 0. ]]
dDividida:
[ 2.569 -1.3163 0.3389 -0.0561 0. ]
polinomio:
2.56896856234546*x - 0.0561488275125463*(x - 3.583)*(x - 2.8008)*(x - 1.3802)*(x - 0.2478)
+ 0.338875729488637*(x - 2.8008)*(x - 1.3802)*(x - 0.2478)
- 1.31628089036375*(x - 1.3802)*(x - 0.2478) + 1.17420959025079
polinomio simplificado:
-0.0561488275125463*x**4 + 0.788728905753656*x**3
- 3.98331084054791*x**2 + 7.41286537452727*x
+ 0.206696844067185
>>>
usando la tabla de diferencias divididas se plantea la expresión para el polinomio:
p(x) = 1.8108 + 2.569 (x-0.2478) +
+ (-1.3163)(x-0.2478)(x-1.3802) +
+ 0.3389 (x-0.2478)(x-1.3802)(x-2.8008) +
+ (-0.0561)(x-0.2478)(x-1.3802)(x-2.8008)(x-3.583)
el algoritmo simplifica la expresión al siguiente polinomio,
p(x) = -0.0561 x^4 + 0.7887 x^3 - 3.9833 x^2 + 7.4128 x + 0.2066
literal c
Se usa el algoritmo Interpolación polinómica de Lagrange con Python para desarrollar el polinomio a partir de los puntos no usados en el literal anterior.
j = [3,4,7,8,9,10]
Para evitar oscilaciones grandes, se excluye el punto con índice 1, y se obtiene una opción mostrada:
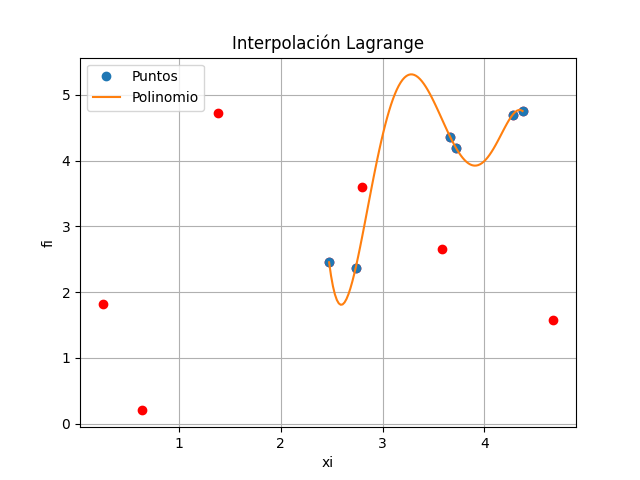
con el siguiente resultado:
valores de fi: [2.4529 2.3644 4.3657 4.1932 4.6998 4.7536]
divisores en L(i): [-1.32578996 0.60430667 -0.02841115 0.02632723 -0.09228243 0.13986517]
Polinomio de Lagrange, expresiones
-1.85014223337671*(x - 4.3757)*(x - 4.2796)*(x - 3.7213)*(x - 3.6627)*(x - 2.7351)
+ 3.9125829809921*(x - 4.3757)*(x - 4.2796)*(x - 3.7213)*(x - 3.6627)*(x - 2.4744)
- 153.661523787291*(x - 4.3757)*(x - 4.2796)*(x - 3.7213)*(x - 2.7351)*(x - 2.4744)
+ 159.272361555669*(x - 4.3757)*(x - 4.2796)*(x - 3.6627)*(x - 2.7351)*(x - 2.4744)
- 50.928437685792*(x - 4.3757)*(x - 3.7213)*(x - 3.6627)*(x - 2.7351)*(x - 2.4744)
+ 33.9870187307222*(x - 4.2796)*(x - 3.7213)*(x - 3.6627)*(x - 2.7351)*(x - 2.4744)
Polinomio de Lagrange:
-9.26814043907703*x**5 + 163.708008152209*x**4
- 1143.16428460497*x**3 + 3941.13583467614*x**2
- 6701.74628786718*x + 4496.64364271972
>>>
Para presentar la parte analítica puede seleccionar menos puntos, se busca mostrar la aplicación del algoritmo, no necesariamente cuan largo puede ser.
p(x) =
+ 2.4529\frac{(x - 4.3757)(x - 4.2796)(x - 3.7213)(x - 3.6627)(x - 2.7351) }{(2.4744 - 4.3757)(2.4744 - 4.2796)(2.4744 - 3.7213)(2.4744 - 3.6627)(2.4744 - 2.7351)}
+ 2.3644\frac{ (x - 4.3757)(x - 4.2796)(x - 3.7213)(x - 3.6627)(x - 2.4744) }{(2.7351 - 4.3757)(2.7351 - 4.2796)(2.7351 - 3.7213)(2.7351 - 3.6627)(2.7351 - 2.4744)}
+4.3657\frac{(x - 4.3757)(x - 4.2796)(x - 3.7213)(x - 2.7351)(x - 2.4744) }{(3.6627 - 4.3757)(3.6627 - 4.2796)(3.6627 - 3.7213)(3.6627 - 2.7351)(3.6627 - 2.4744)}
+ 4.1932 \frac{(x - 4.3757)(x - 4.2796)(x - 3.6627)(x - 2.7351)(x - 2.4744) }{(3.7213 - 4.3757)(3.7213 - 4.2796)(3.7213 - 3.6627)(3.7213 - 2.7351)(3.7213 - 2.4744)}
+4.6998\frac{(x - 4.3757)(x - 3.7213)(x - 3.6627)(x - 2.7351)(x - 2.4744) }{(4.2796 - 4.3757)(4.2796 - 3.7213)(4.2796 - 3.6627)(4.2796 - 2.7351)(4.2796 - 2.4744)}
+ 4.7536 \frac{(x - 4.2796)(x - 3.7213)(x - 3.6627)(x - 2.7351)(x - 2.4744)}{(4.3757 - 4.2796)(4.3757 - 3.7213)(4.3757 - 3.6627)(4.3757 - 2.7351)(4.3757 - 2.4744)}
literal d
las gráficas se han presentado en el planteamiento para justificar los criterios usados.
literal e
Los errores de encuentran como la diferencia de los puntos no usados en el polinomio, y evaluando el polinomio en cada coordenada x.
Como las propuestas de polinomio pueden ser variadas se obtendrán diferentes respuestas para cada literal.
Se revisa la aplicación de conceptos en las propuestas.
Algoritmos usados
literal b. Diferencias divididas de Newton
# 1Eva_2023PAOI_T3 Recoger los restos de sumergible
# Polinomio interpolación
# Diferencias Divididas de Newton
# Tarea: Verificar tamaño de vectores,
# verificar puntos equidistantes en x
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
# INGRESO
xj = np.array([0.2478, 0.6316, 1.3802, 2.4744, 2.7351, 2.8008,
3.5830, 3.6627, 3.7213, 4.2796, 4.3757, 4.6794])
fj = np.array([1.8108, 0.1993, 4.7199, 2.4529, 2.3644, 3.5955,
2.6558, 4.3657, 4.1932, 4.6998, 4.7536, 1.5673])
# selecionando puntos
j = [0, 2, 5, 6, 11]
xi = xj[j]
fi = fj[j]
# PROCEDIMIENTO
# Tabla de Diferencias Divididas Avanzadas
titulo = ['i ','xi ','fi ']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)
# diferencias divididas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)
# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
# Añade título para cada columna
titulo.append('F['+str(j-2)+']')
# cada fila de columna
i = 0
paso = j-2 # inicia en 1
while (i < diagonal):
denominador = (xi[i+paso]-xi[i])
numerador = tabla[i+1,j-1]-tabla[i,j-1]
tabla[i,j] = numerador/denominador
i = i+1
diagonal = diagonal - 1
j = j+1
# POLINOMIO con diferencias Divididas
# caso: puntos equidistantes en eje x
dDividida = tabla[0,3:]
n = len(dfinita)
# expresión del polinomio con Sympy
x = sym.Symbol('x')
polinomio = fi[0]
for j in range(1,n,1):
factor = dDividida[j-1]
termino = 1
for k in range(0,j,1):
termino = termino*(x-xi[k])
polinomio = polinomio + termino*factor
# simplifica multiplicando entre (x-xi)
polisimple = polinomio.expand()
# polinomio para evaluacion numérica
px = sym.lambdify(x,polisimple)
# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)
# SALIDA
np.set_printoptions(precision = 4)
print('Tabla Diferencia Dividida')
print([titulo])
print(tabla)
print('dDividida: ')
print(dDividida)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)
# Gráfica
plt.plot(xj,fj,'o',color='red')
plt.plot(xi,fi,'o', label = 'Puntos')
##for i in range(0,n,1):
## plt.axvline(xi[i],ls='--', color='yellow')
plt.plot(pxi,pfi, label = 'Polinomio')
plt.legend()
plt.grid()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Diferencias Divididas - Newton')
plt.show()
literal c. Polinomio de Lagrange
# 1Eva_2023PAOI_T3 Recoger los restos de sumergible
# Interpolacion de Lagrange
# divisoresL solo para mostrar valores
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
# INGRESO , Datos de prueba
xj = np.array([0.2478, 0.6316, 1.3802, 2.4744, 2.7351, 2.8008,
3.5830, 3.6627, 3.7213, 4.2796, 4.3757, 4.6794])
fj = np.array([1.8108, 0.1993, 4.7199, 2.4529, 2.3644, 3.5955,
2.6558, 4.3657, 4.1932, 4.6998, 4.7536, 1.5673])
# selecionando puntos
#j = [0, 2, 5, 6, 11]
j = [3,4,7,8,9,10]
xi = xj[j]
fi = fj[j]
# PROCEDIMIENTO
# Polinomio de Lagrange
n = len(xi)
x = sym.Symbol('x')
polinomio = 0
divisorL = np.zeros(n, dtype = float)
for i in range(0,n,1):
# Termino de Lagrange
numerador = 1
denominador = 1
for j in range(0,n,1):
if (j!=i):
numerador = numerador*(x-xi[j])
denominador = denominador*(xi[i]-xi[j])
terminoLi = numerador/denominador
polinomio = polinomio + terminoLi*fi[i]
divisorL[i] = denominador
# simplifica el polinomio
polisimple = polinomio.expand()
# para evaluación numérica
px = sym.lambdify(x,polisimple)
# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)
# SALIDA
print(' valores de fi: ',fi)
print('divisores en L(i): ',divisorL)
print()
print('Polinomio de Lagrange, expresiones')
print(polinomio)
print()
print('Polinomio de Lagrange: ')
print(polisimple)
# Gráfica
plt.plot(xj,fj,'o',color='red')
plt.plot(xi,fi,'o', label = 'Puntos')
plt.plot(pxi,pfi, label = 'Polinomio')
plt.legend()
plt.grid()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Interpolación Lagrange')
plt.show()