Ejercicio: 1Eva_IT2009_T2 Materiales y Productos 3×4
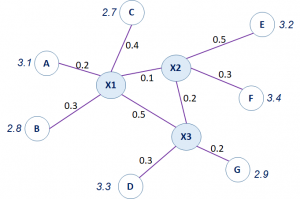
Con los datos de la tabla se plantean las ecuaciones:
|
P1 |
P2 |
P3 |
P4 |
| M1 |
0.2 |
0.5 |
0.4 |
0.2 |
| M2 |
0.3 |
0 |
0.5 |
0.6 |
| M3 |
0.4 |
0.5 |
0.1 |
0.2 |
La cantidad disponible de cada material es: 10, 12, 15 Kg respectivamente, los cuales deben usarse completamente.
1. Plantear el sistema de ecuaciones
0.2 x_0 + 0.5 x_1 + 0.4 x_2 + 0.2 x_3 = 10
0.3 x_0 + 0 x_1 + 0.5 x_2 + 0.6 x_3 = 12
0.4 x_0 + 0.5 x_1 + 0.1 x_2 + 0.2 x_3 = 15
Observe que hay más incógnitas que ecuaciones.
Para equiparar las ecuaciones con el número de incógnitas, podríamos suponer que uno de los productos NO se fabricará. por ejemplo el producto x3 que podría hacerse igual a cero. Supone que la variable libre es x3 .
Para mantener la forma de las ecuaciones para otros valores de x3, se pasa la variable y su coeficiente a la derecha.
\begin{cases} 0.2 x_0 + 0.5 x_1 + 0.4 x_2 = 10 - 0.2 x_3 \\ 0.3 x_0 + 0 x_1 + 0.5 x_2 = 12 - 0.6 x_3 \\ 0.4 x_0 + 0.5 x_1 + 0.1 x_2 = 15 - 0.2 x_3 \end{cases}
Para analizar el ejercicio, se supondrá que el valor de x3 = 0, lo que permite usar el modelo del problema como A.X=B .En caso de que x3 sea diferente de cero, el vector B modifica, y se puede proceder con el sistema de ecuaciones.
2. Convertir a la forma matricial AX = B
Siendo así, suponiendo que x3 = 0, el ejercicio se puede desarrollar usando:
\begin{pmatrix} 0.2 && 0.5 &&0.4 &&10 \\ 0.3 && 0. && 0.5 && 12.\\ 0.4 && 0.5 && 0.1 && 15. \end{pmatrix}
que de debe pivotear por filas antes de aplicar cualquier método de solución, primero se intercambian la primera y última filas para que el primer valor de la diagonal sea el mayor en la columna.
\begin{pmatrix} 0.4 && 0.5 && 0.1 && 15. \\ 0.3 && 0. && 0.5 && 12. \\0.2 && 0.5 &&0.4 &&10 \end{pmatrix}
luego se repite el proceso a partir de la diagonal en la fila segunda, columna segunda, que al tener un valor de 5 en la tercera fila que es mayor que 0, se intercambia la fila segunda con la tercera
\begin{pmatrix} 0.4 && 0.5 && 0.1 && 15. \\0.2 && 0.5 &&0.4 &&10 \\ 0.3 && 0. && 0.5 && 12. \end{pmatrix}
Para el proceso de eliminación hacia adelante se tiene:
para pivote[0,0] = 0.4,
fila = 0 vs fila 1:
pivote = 0.4, factor = 0.2/0.4 = 0.5
\begin{pmatrix} 0.4 && 0.5 && 0.1 && 15. \\0 && 0.25 &&0.35 &&2.5 \\ 0.3 && 0. && 0.5 && 12. \end{pmatrix}
fila = 0 vs fila 2:
pivote = 0.4, factor = 0.3/0.4 = 0.75
\begin{pmatrix} 0.4 && 0.5 && 0.1 && 15. \\0 && 0.25 &&0.35 &&2.5 \\ 0 && -0.375 && 0.425 && 0.75 \end{pmatrix}
y luego para pivote [1,1]
fila = 1 vs fila 2:
pivote = 0.25, factor =-0.375/0.25 = -1.5
\begin{pmatrix} 0.4 && 0.5 && 0.1 && 15. \\0 && 0.25 &&0.35 &&2.5 \\ 0 && 0. && 0.95 && 4.5 \end{pmatrix}
Para eliminación hacia atrás los factores serán:
fila 2 pivote: 0.95
factor: 0.368421052631579 para fila: 1
factor: 0.10526315789473685 para fila: 0
\begin{pmatrix} 0.4 && 0.5 && 0 && 14.52631579 \\0 && 0.25 &&0 &&0.84210526 \\ 0 && 0. && 0.95 && 4.5 \end{pmatrix}
fila 1 pivote: 0.25
factor: 2.0 para fila: 0
\begin{pmatrix} 0.4 && 0 && 0 && 12.84210526 \\0 && 0.25 &&0 &&0.84210526 \\ 0 && 0. && 0.95 && 4.5 \end{pmatrix}
lo que da como resultado:
\begin{pmatrix} 1 && 0 && 0 && 32.10526316 \\0 && 1 &&0 &&3.36842105 \\ 0 && 0 && 1 && 4.73684211 \end{pmatrix}
que da como solución:
x= [32.10526316, 3.36842105 , 4.73684211]
Algoritmo en Python
Para el algoritmo se puede empezar con:
A = np.array([[0.2, 0.5, 0.4],
[0.3, 0.0, 0.5],
[0.4, 0.5, 0.1]])
B = np.array([10, 12, 15],dtype=float)
que luego armar el algoritmo y su ejecución, obtendría una solución semejante:
Matriz aumentada
[[ 0.2 0.5 0.4 10. ]
[ 0.3 0. 0.5 12. ]
[ 0.4 0.5 0.1 15. ]]
Pivoteo parcial:
1 intercambiar filas: 0 y 2
2 intercambiar filas: 1 y 2
[[ 0.4 0.5 0.1 15. ]
[ 0.2 0.5 0.4 10. ]
[ 0.3 0. 0.5 12. ]]
Elimina hacia adelante:
fila 0 pivote: 0.4
factor: 0.5 para fila: 1
factor: 0.7499999999999999 para fila: 2
fila 1 pivote: 0.25
factor: -1.4999999999999998 para fila: 2
fila 2 pivote: 0.95
[[ 0.4 0.5 0.1 15. ]
[ 0. 0.25 0.35 2.5 ]
[ 0. 0. 0.95 4.5 ]]
Elimina hacia Atras:
fila 2 pivote: 0.95
factor: 0.368421052631579 para fila: 1
factor: 0.10526315789473685 para fila: 0
fila 1 pivote: 0.25
factor: 2.0 para fila: 0
fila 0 pivote: 0.4
[[ 1. 0. 0. 32.10526316]
[ 0. 1. 0. 3.36842105]
[ 0. 0. 1. 4.73684211]]
solución X:
[32.10526316 3.36842105 4.73684211]
>>>
Instrucciones en Python
#1Eva_IT2009_T2 Materiales y Productos 3×4
# Método de Gauss-Jordan
# Solución a Sistemas de Ecuaciones
# de la forma A.X=B
import numpy as np
def pivoteafila(A,B,vertabla=False):
'''
Pivotea parcial por filas
Si hay ceros en diagonal es matriz singular,
Tarea: Revisar si diagonal tiene ceros
'''
A = np.array(A,dtype=float)
B = np.array(B,dtype=float)
# Matriz aumentada
nB = len(np.shape(B))
if nB == 1:
B = np.transpose([B])
AB = np.concatenate((A,B),axis=1)
if vertabla==True:
print('Matriz aumentada')
print(AB)
print('Pivoteo parcial:')
# Pivoteo por filas AB
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
# Para cada fila en AB
pivoteado = 0
for i in range(0,n-1,1):
# columna desde diagonal i en adelante
columna = np.abs(AB[i:,i])
dondemax = np.argmax(columna)
# dondemax no es en diagonal
if (dondemax != 0):
# intercambia filas
temporal = np.copy(AB[i,:])
AB[i,:] = AB[dondemax+i,:]
AB[dondemax+i,:] = temporal
pivoteado = pivoteado + 1
if vertabla==True:
print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax+i)
if vertabla==True:
if pivoteado==0:
print(' Pivoteo por filas NO requerido')
else:
print(AB)
return(AB)
def gauss_eliminaAdelante(AB, vertabla=False,lu=False,casicero = 1e-15):
''' Gauss elimina hacia adelante, a partir de,
matriz aumentada y pivoteada.
Para respuesta en forma A=L.U usar lu=True entrega[AB,L,U]
'''
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
L = np.identity(n,dtype=float) # Inicializa L
if vertabla==True:
print('Elimina hacia adelante:')
for i in range(0,n,1):
pivote = AB[i,i]
adelante = i+1
if vertabla==True:
print(' fila',i,'pivote: ', pivote)
for k in range(adelante,n,1):
if (np.abs(pivote)>=casicero):
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - factor*AB[i,:]
L[k,i] = factor # llena L
if vertabla==True:
print(' factor: ',factor,' para fila: ',k)
print(AB)
else:
print(' pivote:', pivote,'en fila:',i,
'genera division para cero')
respuesta = AB
if vertabla==True:
print(AB)
if lu==True:
U = AB[:,:n-1]
respuesta = [AB,L,U]
return(respuesta)
def gauss_eliminaAtras(AB, vertabla=False, precision=5, casicero = 1e-15):
''' Gauss-Jordan elimina hacia atras
Requiere la matriz triangular inferior
Tarea: Verificar que sea triangular inferior
'''
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
ultfila = n-1
ultcolumna = m-1
if vertabla==True:
print('Elimina hacia Atras:')
for i in range(ultfila,0-1,-1):
pivote = AB[i,i]
atras = i-1 # arriba de la fila i
if vertabla==True:
print(' fila',i,'pivote: ', pivote)
for k in range(atras,0-1,-1):
if (np.abs(AB[k,i])>=casicero):
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - factor*AB[i,:]
if vertabla==True:
print(' factor: ',factor,' para fila: ',k)
else:
print(' pivote:', pivote,'en fila:',i,
'genera division para cero')
AB[i,:] = AB[i,:]/AB[i,i] # diagonal a unos
X = np.copy(AB[:,ultcolumna])
if vertabla==True:
print(AB)
return(X)
# PROGRAMA ------------------------
# INGRESO
A = np.array([[0.2, 0.5, 0.4],
[0.3, 0.0, 0.5],
[0.4, 0.5, 0.1]])
B = np.array([10, 12, 15],dtype=float)
# PROCEDIMIENTO
AB = pivoteafila(A,B,vertabla=True)
AB = gauss_eliminaAdelante(AB,vertabla=True)
X = gauss_eliminaAtras(AB,vertabla=True)
# SALIDA
print('solución X: ')
print(X)
Encontrada la solución, modifique el algoritmo para calcular B en función de x3, pregunte el valor al inicio, y vuelva a calcular.
x3 = float(input('cantidad a producir de cuarto producto: ')
Observe el rango para x3, por ejemplo que debe ser mayor o igual que cero, pues no hay producción negativa. De producir solamente ése un producto, el valor máximo de unidades a obtener no superaría lo posible con la cantidad de materiales disponible.
Ejemplo:
x3 = 1
B3 = [0.2,0.6,0.2]
Bnuevo = B - x3*B3
>>> Bnuevo
array([ 9.8, 11.4, 14.8])
Y se vuelve a generar el sistema A.X=Bnuevo
Observación: Algunos productos se fabrican por unidades, no necesariamente por peso o volumen. ¿comentarios al respecto?