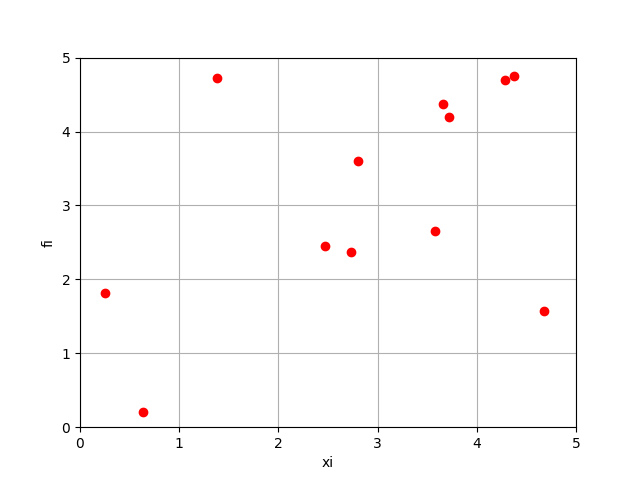
Ejercicio: 1Eva_2025PAOI_T2 Cables de cámara aérea

literal a. matriz aumentada y pivoteo parcial por filas

Las ecuaciones que conforman el sistema de ecuaciones son:

\frac{55}{56.75} T_{AB} - \frac{60}{71.36} T_{AD}=0 \frac{14}{56.75} T_{AB} + \frac{14}{34.93} T_{AC} + \frac{14}{71.36} T_{AD}-490=0 -\frac{32}{34.93} T_{AC} + \frac{36}{71.36} T_{AD}=0

Se reordenan las ecuaciones para la forma A.X=B, con las constantes del lado derecho.

\frac{55}{56.75} T_{AB} - \frac{60}{71.36} T_{AD}=0 \frac{14}{56.75} T_{AB} + \frac{14}{34.93} T_{AC} + \frac{14}{71.36} T_{AD} =490 -\frac{32}{34.93} T_{AC} + \frac{36}{71.36} T_{AD}=0

la matriz A y vector B serán:

A = \begin{pmatrix} \frac{55}{56.75} &0& - \frac{60}{71.36} \\ \frac{14}{56.75} &\frac{14}{34.93} &\frac{14}{71.36} \\ 0 &-\frac{32}{34.93}& \frac{36}{71.36}\end{pmatrix} B =[0,490,0]

Matriz Aumentada

\left( \begin{array}{rrr|r} \frac{55}{56.75} &0& - \frac{60}{71.36} & 0\\ \frac{14}{56.75} & \frac{14}{34.93} & \frac{14}{71.36} &490\\ 0 &-\frac{32}{34.93} & \frac{36}{71.36} & 0\end{array} \right)

Pivoteo parcial por filas

columna = 0, no requiere cambios, la mayor magnitud se encuentra en la diagonal.

columna = 1

\left( \begin{array}{rrr|r} \frac{55}{56.75} &0& - \frac{60}{71.36} & 0\\ 0 &-\frac{32}{34.93} & \frac{36}{71.36} & 0 \\ \frac{14}{56.75} & \frac{14}{34.93} & \frac{14}{71.36} &490\end{array} \right)

literal b. Expresiones para método Jacobi

fila = 0
\frac{55}{56.75} x + 0 y - \frac{60}{71.36} z =0

\frac{55}{56.75} x = \frac{60}{71.36} z x = \frac{60}{71.36} z \left(\frac{1}{\frac{55}{56.75}}\right) x = \frac{60(56.75)}{71.36(55)}z =0.86756 z

fila = 1

0 x -\frac{32}{34.93} y + \frac{36}{71.36} z = 0 -\frac{32}{34.93} y = - \frac{36}{71.36} z y = \frac{36}{71.36} z \left(\frac{1}{\frac{32}{34.93}}\right) y = \frac{36(34.93)}{71.36(32)} z = 0.55067 z/

fila = 2

\frac{14}{56.75} x + \frac{14}{34.93} y + \frac{14}{71.36} z = 490 \frac{14}{71.36} z = 490 -\frac{14}{56.75} x -\frac{14}{34.93} y z = \left( 490 -\frac{14}{56.75} x -\frac{14}{34.93} y \right) \frac{1}{ \frac{14}{71.36}} z = \left( 490 -\frac{14}{56.75} x -\frac{14}{34.93} y \right) \frac{71.36}{14}

expresiones para el método:

x = 0.86756 z y = 0.55067 z z = \left( 490 -\frac{14}{56.75} x -\frac{14}{34.93} y \right) (5.09714)

literal c. Iteraciones Jacobi

Si la cámara tiene un peso de 490, cuelga de 3 cables, en el mejor de los casos cada cable tendría una tensión de 1/3 del peso. Por lo que el vector inicial X0=[490/3,490/3,490/3]

x = 0.86756 z y = 0.55067 z z = \left( 490 -\frac{14}{56.75} x -\frac{14}{34.93} y \right) (5.09714)

itera = 0

X0=[490/3,490/3,490/3]

x = 0.86756 (490/3) = 141.7014 y = 0.55067 (490/3) = 89.9427 z = \left( 490 -\frac{14}{56.75} (490/3) -\frac{14}{34.93} (490/3) \right) (5.09714) z =1958.53

X1 = [141.7014, 89.9427, 1958.5366]

 X1:  [141.7014, 89.9427, 1958.5366]
-X0: -[490/3,    490/3,   490/3    ]
____________________________________
dif:  [21.63185  73.38956 1795.2033 ]
errado = max(abs(diferencia) = 1795.20

itera = 1

x = 0.86756 (1958.5366)=1699.1483 y = 0.55067 (1958.5366)= 1078.51941 z = \left( 490 -\frac{14}{56.75} (141.7014) -\frac{14}{34.93} (89.9427) \right) (5.09714) z=2135.66818

X2= [1699.1483, 1078.51941, 2135.66818]

 X2:  [1699.1483, 1078.51941, 2135.66818]
-X1: -[ 141.7014,   89.9427,  1958.5366 ]
_________________________________________
dif:  [1557.44681  988.57564   177.13155]
errado = max(abs(diferencia) = 1557.44681

itera = 2

x = 0.86756 (2135.66818)=1852.82057 y = 0.55067 (2135.66818)=1176.06153 z = \left( 490 -\frac{14}{56.75} (1699.1483) -\frac{14}{34.93} (1078.51941) \right) (5.09714) z =-1842.33913

X3= [1852.82057, 1176.06153, -1842.33913]

 X3:  [1852.82057, 1176.06153, -1842.33913]
-X2: -[1699.1483,  1078.51941,  2135.66818]
____________________________________________
dif:  [ 153.67227   97.54212 3978.00731]
errado = max(abs(diferencia) = 3978.00731

literal d. convergencia

Se observa que el error aumenta en cada iteración, por lo que el método NO converge.

En la tercera iteración, la Tensión AD es negativa, lo que no tiene sentido en el contexto del ejercicio.

literal e. Número de condición

el número de condición calculado es:

numero de condición: 3.254493400285106

literal f. resultados con algoritmo

los resultados de las iteraciones con el algoritmo son:

Matriz aumentada
[[ 9.6916299e-01  0.0000000e+00 -8.4080717e-01  0.000e+00]
 [ 2.4669603e-01  4.0080160e-01  1.9618834e-01  4.900e+02]
 [ 0.0000000e+00 -9.1611795e-01  5.0448430e-01  0.000e+00]]
Pivoteo parcial:
  1 intercambiar filas:  1 y 2
AB
Iteraciones Jacobi
itera,[X]
     ,errado,|diferencia|
0 [163.33333333 163.33333333 163.33333333]
  nan
1 [ 141.70149   89.94377 1958.53663]
  1795.203299403506 [  21.63185   73.38956 1795.2033 ]
2 [1699.1483  1078.51941 2135.66818]
  1557.446808619277 [1557.44681  988.57564  177.13155]
3 [ 1852.82057  1176.06153 -1842.33913]
  3978.007311178223 [ 153.67227   97.54212 3978.00731]
4 [-1598.33998 -1014.53222 -2234.84654]
  3451.1605418268064 [3451.16054 2190.59375  392.50741]
5 [-1938.86376 -1230.67669  6580.05603]
  8814.902564542654 [ 340.52378  216.14447 8814.90256]
6 [5708.59426 3623.47991 7449.81676]
  7647.458018820763 [7647.45802 4854.1566   869.76074]
7 [  6463.164     4102.43641 -12083.20597]
  19533.02272824792 [  754.56974   478.95649 19533.02273]
8 [-10482.90774  -6653.93333 -14010.51669]
  16946.071746250553 [16946.07175 10756.36974  1927.31073]
9 [-12154.96569  -7715.25738  29272.88595]
  43283.40263645846 [ 1672.05794  1061.32405 43283.40264]
10 [25395.98875 16119.88011 33543.6313 ]
  37550.95443771429 [37550.95444 23835.13748  4270.74536]
11 [ 29101.11715  18471.67771 -62368.45408]
  95912.08538760681 [ 3705.1284   2351.79761 95912.08539]
12 [-54108.38416 -34344.82012 -71832.03755]
  83209.50131084416 [83209.50131 52816.49783  9463.58346]
13 [-62318.61187 -39556.18982 140700.42439]
  212532.4619384469 [  8210.22771   5211.3697  212532.46194]
14 [122066.07854  77480.36788 161670.86502]
  184384.6904047115 [184384.6904  117036.5577   20970.44063]
15 [ 140259.19675   89028.28937 -309281.7495 ]
  470952.61452269484 [ 18193.11821  11547.92149 470952.61452]
16 [-268320.51494 -170314.0828  -355750.33954]
  408579.7116922584 [408579.71169 259342.37218  46468.59004]
No converge,iteramax superado
Metodo de Jacobi
numero de condición: 3.254493400285106
X:  nan
errado: 408579.7116922584
iteraciones: 16

las gráficas de las iteraciones son:

la gráfica de errores por iteración

 

Ejercicio: 1Eva_2025PAOI_T1 Recargar combustible en órbita

literal a. Planteamiento

Según el enunciado, se plantea el ejercicio primero para el eje y. Cuando las coordenadas de ambos son iguales en el eje y.

T_y (t) = 2\cos(3.5t) S_y (t) = 2 - 2e^{(-9t)} T_y (t) = S_y (t) 2\cos(3.5t) =2 - 2e^{(-9t)} 2 - 2e^{(-9t)} -2\cos(3.5t) = 0 f(t) = 2 - 2e^{(-9t)} -2\cos(3.5t)

literal b. Intervalo [a,b]

Las gráficas presentadas en el enunciado, confirman que existe una raíz en el intervalo 0 ≤ t ≤ (π/7). Se verifica revisando el signo de f(t) en los extremos del intervalo:

f(0) = 2 - 2e^{(-9(0))} -2\cos(3.5(0)) =-2 f(π/7) = 2 - 2e^{(-9(π/7))} -2\cos(3.5(π/7))=1.9647

Los resultados tienen signos opuestos, lo que confirma que existe al menos una raíz en el intervalo.

literal c. Método de Newton-Raphson

En éste método se requiere de la derivada f'(t)

f(t) = 2 - 2e^{(-9t)} -2\cos(3.5t) f'(t) = 18e^{(-9t)} +2(3.5)\sin(3.5t)

import sympy as sym
t = sym.Symbol('t')
f = 2-2*sym.exp(-9*t)-2*sym.cos(3.5*t)
df = sym.diff(f,t,1)
print(df)

resultado:

7.0*sin(3.5*t) + 18*exp(-9*t)

itera = 0

el punto inicial de búsqueda puede ser x₀=0.1, que se encuentra dentro del intervalo

f(0.1) = 2 - 2e^{(-9(0.1))} -2\cos(3.5(0.1)) = -0.6918 f'(0.1) = 18e^{(-9(0.1))} +2(3.5)\sin(3.5(0.1)) = 9.7185 x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 0.1 - \frac{-0.6918}{9.7185} =0.1711 tramo = |0.1711-0.1| = 0.0711

itera = 1

x₁= 0.1711

f(0.1711) = 2 -2e^{(-9(0.1711))} -2\cos(3.5(0.1711)) =-0.08005 f'(0.1711) = 18e^{(-9(0.1711))} + 2(3.5)\sin(3.5(0.1711))=7.8037 x_1 = 0.1711 - \frac{-0.08005}{7.8037} =0.1814 tramo = |0.1814-0.1711| = 0.0102

itera = 2
x₂= 0.1814

f(0.1814) = 2 -2e^{(-9(0.1814))} -2\cos(3.5(0.1814)) =-0.0003660 f'(0.1814) = 18e^{(-9(0.1814))} + 2(3.5)\sin(3.5(0.1814)) =7.9654 x_1 = 0.1814 - \frac{-0.0003660}{7.9654} = 0.1815 tramo = |0.1815-0.1814| = 0.0001

literal d y e. Errores por iteración

En el desarrollo se muestran los errores como tramos. Se observa que los errores disminuyen en cada iteración, por lo que se considera que el método converge.  El error de la última iteración es del orden de 10^-4, lo que es menor que la  tolerancia 10^-3. por lo que la raíz será: 0.1815

Nota: el algoritmo lo obtiene del blog y lo modifica para el ejercicio, obteniendo los datos de las operaciones

Resultados con el algoritmo:

i: 1 fi: -0.691884745175956 dfi: 9.718538527518945
   xnuevo: 0.171192262418554 tramo: 0.071192262418554
i: 2 fi: -0.08005384152091866 dfi: 7.803760114465353
   xnuevo: 0.18145063022416194 tramo: 0.010258367805607932
i: 3 fi: -0.0007153774553945169 dfi: 7.668649926460424
   xnuevo: 0.18154391619525917 tramo: 9.328597109722891e-05
raiz en:  0.18154391619525917
con error de:  9.328597109722891e-05

Gráfica f(t) = Sy(t) – Ty(t)

---

literal f. Encontrar k en Sx(t) = Tx(t)

Se usan las ecuaciones en eje x con el valor encontrado t=0.1815.

No se indica desarrollar el ejercicio en papel y lápiz, por lo que la respuesta es solo con el algoritmo, por ejemplo, bisección.

T_x (t) = 2\sin(3.5t) S_x (t) = 3.2(t+k)+4.1(t+k)^2 T_x (t) = S_x (t) 2\sin(3.5t) = 3.2(t+k)+4.1(t+k)^2 3.2(t+k)+4.1(t+k)^2-2\sin(3.5t) =0 3.2(0.1815+k)+4.1(0.1815+k)^2 -2\sin(3.5(0.1815))=0 f(k) = 3.2(0.1815+k)+4.1(0.1815+k)^2 - 2\sin(3.5(0.1815))

que da una función dependiente de k, usando el método de la bisección, para el intervalo [0,π/7] y tolerancia del ejercicio anterior, siempre que exista cambio de signo se prueba:

i: 0 a: 0 c: 0.2243994752564138 b: 0.4487989505128276
  fa: -0.4709358324617918 fc: 0.7876530469374095 fb: 2.459153947198512 tramo: 0.2243994752564138
i: 1 a: 0 c: 0.1121997376282069 b: 0.2243994752564138
  fa: -0.4709358324617918 fc: 0.10674460463007107 fb: 0.7876530469374095 tramo: 0.1121997376282069
i: 2 a: 0 c: 0.05609986881410345 b: 0.1121997376282069
  fa: -0.4709358324617918 fc: -0.19499911456779484 fb: 0.10674460463007107 tramo: 0.05609986881410345
i: 3 a: 0.05609986881410345 c: 0.08414980322115517 b: 0.1121997376282069
  fa: -0.19499911456779484 fc: -0.0473531301318455 fb: 0.10674460463007107 tramo: 0.028049934407051724
i: 4 a: 0.08414980322115517 c: 0.09817477042468103 b: 0.1121997376282069
  fa: -0.0473531301318455 fc: 0.028889268458366812 fb: 0.10674460463007107 tramo: 0.014024967203525862
i: 5 a: 0.08414980322115517 c: 0.0911622868229181 b: 0.09817477042468103
  fa: -0.0473531301318455 fc: -0.009433548034425865 fb: 0.028889268458366812 tramo: 0.007012483601762931
i: 6 a: 0.0911622868229181 c: 0.09466852862379957 b: 0.09817477042468103
  fa: -0.009433548034425865 fc: 0.00967745591254876 fb: 0.028889268458366812 tramo: 0.0035062418008814655
i: 7 a: 0.0911622868229181 c: 0.09291540772335884 b: 0.09466852862379957
  fa: -0.009433548034425865 fc: 0.00010935286420599155 fb: 0.00967745591254876 tramo: 0.0017531209004407328
i: 8 a: 0.0911622868229181 c: 0.09203884727313846 b: 0.09291540772335884
  fa: -0.009433548034425865 fc: -0.0046652478538238285 fb: 0.00010935286420599155 tramo: 0.0008765604502203733
       raiz en:  0.09203884727313846
error en tramo:  0.0008765604502203733

se encuentra k = 0.09203

Ejercicio: s1Eva_2024PAOII_T3 matriz de distribución de energía por sectores

:

Fuente\Consumidor	Industrial	Comercial	Transporte	Residencial
Hidroeléctrica	0.7	0.19	0.1	0.01
Gas Natural	0.12	0.18	0.68	0.02
Petróleos-combustible	0.2	0.38	0.4	0.02
Eólica	0.11	0.23	0.15	0.51

total de fuente de generación para la tabla es: [1500,400,600,200]

literal a Planteamiento

Considerando que el factor de la tabla es el factor de consumo por tipo de cliente, para encontrar las cantidades por tipo cliente que se puedan atender con la capacidad de cada «fuente de generación», se plantea:

0.7x+0.19y+0.1z+0.01w = 1500 0.12x+0.18y+0.68z+0.02w = 400 0.2x+0.38y+0.4z+0.04w = 600 0.11x+0.23y+0.15z+0.51w =200

literal b. Matriz aumentada y Pivoteo parcial por filas

\begin{bmatrix} 0.7 & 0.19& 0.1 & 0.01 &1500 \\ 0.12 & 0.18 & 0.68 & 0.02 & 400 \\0.2 & 0.38 & 0.4 & 0.02 & 600 \\0.11 & 0.23& 0.15 & 0.51 & 200 \end{bmatrix}

Revisando la primera columna j=0,  el mayor valor ya se encuentra en la posición de la diagonal i=0, por lo que no hay cambio de filas

Para la segunda columna j=1, desde la posición de la diagonal i=1, el mayor valor se encuentra en i=2, por lo que intercambian las filas.

\begin{bmatrix} 0.7 & 0.19& 0.1 & 0.01 &1500\\0.2 & 0.38 & 0.4 & 0.02 & 600 \\ 0.12 & 0.18 & 0.68 & 0.02 & 400 \\ 0.11 & 0.23& 0.15 & 0.51 & 200 \end{bmatrix}

Al observar la tercera columna j=2, desde la diagonal i=2, el valor mayor ya se encuentra en la posición de la diagonal, no hay cambio de filas. Para la última fila no se tiene otra fila para comparar, con lo que el pivoteo se terminó.

literal c. Método de Jacobi

A partir de la matriz del literal anterior, las expresiones quedan:

0.7x+0.19y+0.1z+0.01w = 1500 0.2x+0.38y+0.4z+0.04w = 600 0.12x+0.18y+0.68z+0.02w = 400 0.11x+0.23y+0.15z+0.51w =200

y despejar una incógnita de cada ecuación se convierte en:

x = \frac{1}{0.7} \Big( 1500 - (+0.19y+0.1z+0.01w) \Big) y = \frac{1}{0.38} \Big( 600 - (0.2x +0.4z+0.04w) \Big) z = \frac{1}{0.68} \Big(400-(0.12x+0.18y+0.02w)\Big) w =\frac{1}{0.51} \Big(200-(0.11x+0.23y+0.15z) \Big)

literal d. iteraciones

En el literal c, se sugiere iniciar con el vector X₀ = [100,100,100,100].

Como la unidad de medida en las incógnitas es número de clientes, la tolerancia puede ajustarse a 0.1.

itera = 0

X₀ = [100,100,100,100]

x = \frac{1}{0.7} \Big( 1500 - (+0.19(100)+0.1(100)+0.01(100)) \Big) = 2100 y = \frac{1}{0.38} \Big( 600 - (0.2(100) +0.4(100)+0.04(100)) \Big) = 1415.7 z = \frac{1}{0.68} \Big(400-(0.12(100)+0.18(100)+0.02(100))\Big) = 541.17 w =\frac{1}{0.51} \Big(200-(0.11(100)+0.23(100)+0.15(100)) \Big) =296.1 errado = max| [ 2100-100, 1415.7-100, 541.17-100, 296.1-100] | errado = max| [ 2000, 1315.7,441.17,196.1] | = 2000

itera = 1

X₀ = [ 2100, 1415.7, 541.1, 296.1 ]

x = \frac{1}{0.7} \Big( 1500 - (+0.19(1415.7)+0.1(541.1)+0.01(296.1)) \Big) = 1677.0 y = \frac{1}{0.38} \Big( 600 - (0.2(2100) +0.4(541.1)+0.04( 296.1)) \Big) = -111.55 z = \frac{1}{0.68} \Big(400-(0.12(2100)+0.18(1415.7)+0.02(541.1))\Big) = -165.82 w =\frac{1}{0.51} \Big(200-(0.11( 2100)+0.23( 1415.7)+0.15(541.1)) \Big) =-858.44 errado = max| [ 1677.0 - 2100,-111.55 -1415.7, -165.82- 541.17, -858.44- 296.1] | errado = max| [ -423, -1527.25 ,-706.99 ,-1154.54] | = 1527.25

itera = 2

tarea..

literal e. convergencia y revisión de resultados obtenidos

Para el asunto de convergencia, el error disminuye entre iteraciones, por lo que el método es convergente.

Analizando los resultados desde la segunda iteración, se obtienen valores negativos, lo que no es acorde al concepto del problema. Se continuarán con las iteraciones siguientes y se observará el resultado para dar mayor «opinión» sobre lo obtenido.

literal f Número de condición

Número de condición = 5.77 que al ser «bajo y cercano a 1» se considera que el método converge.

Resultados con el algoritmo

Iteraciones Jacobi
itera,[X],errado
0 [100. 100. 100. 100.] 1.0
1 [2100.      1415.78947  541.17647  296.07843] 2000.0
2 [1677.03081 -111.55831 -165.82893 -858.44716] 1527.3477812177503
3 [2209.09063  916.03777  347.06727  129.52816] 1027.5960799832396
4 [1842.78688   44.11685  -47.89447 -599.50735] 871.9209205662409
5 [2146.28903  691.02779  268.99219  -11.1162 ] 646.9109334007268
...
40 [2022.87519  383.13614  137.36642 -257.41944] 0.11802984805018468
41 [2022.91669  383.22837  137.41009 -257.33833] 0.09223623893257127
numero de condición: 5.7772167744910625
respuesta X: 
[2022.91669  383.22837  137.41009 -257.33833]
iterado, incluyendo X0:  42

El resultado muestra que los clientes residenciales serán -257 según las ecuaciones planteadas. Lo que se interpreta según lo presentado por los estudiantes:

1. energía insuficiente: causa por los apagones diarios en el país en éstos días.

2. Se requiere mejorar el planteamiento, pues la respuesta no debe contener valores negativos según el concepto planteado en el ejercicio.

Se considerarán ambas válidas para la evaluación al observar que el resultado numérico es correcto, pero no es acorde al ejercicio.

 

Instrucciones en Python

# 1Eva_2024PAOII_T3 matriz de distribución de energía por sectores
import numpy as np

#INGRESO
A= [[0.7,0.19,0.1,0.01],
    [0.12,0.18,0.68,0.02],
    [0.2,0.38,0.4,0.02],
    [0.11,0.23,0.15,0.51]]

B = [1500,400,600,200]

# PROCEDIMIENTO
A = np.array(A,dtype=float)
B = np.transpose([np.array(B)])

X0 = [100,100,100,100]
tolera = 0.1
iteramax = 100
verdecimal = 5

def jacobi(A,B,X0, tolera, iteramax=100, vertabla=False, precision=4):
    ''' Método de Jacobi, tolerancia, vector inicial X0
        para mostrar iteraciones: vertabla=True
    '''
    A = np.array(A,dtype=float)
    B = np.array(B,dtype=float)
    X0 = np.array(X0,dtype=float)
    tamano = np.shape(A)
    n = tamano[0]
    m = tamano[1]
    diferencia = np.ones(n, dtype=float)
    errado = np.max(diferencia)
    X = np.copy(X0)
    xnuevo = np.copy(X0)
    tabla = [np.copy(X0)]

    itera = 0
    if vertabla==True:
        print('Iteraciones Jacobi')
        print('itera,[X],errado')
        print(itera, xnuevo, errado)
        np.set_printoptions(precision)
    while not(errado<=tolera or itera>iteramax):
        
        for i in range(0,n,1):
            nuevo = B[i]
            for j in range(0,m,1):
                if (i!=j): # excepto diagonal de A
                    nuevo = nuevo-A[i,j]*X[j]
            nuevo = nuevo/A[i,i]
            xnuevo[i] = nuevo
        diferencia = np.abs(xnuevo-X)
        errado = np.max(diferencia)
        X = np.copy(xnuevo)
        
        tabla = np.concatenate((tabla,[X]),axis = 0)

        itera = itera + 1
        if vertabla==True:
            print(itera, xnuevo, errado)

    # No converge
    if (itera>iteramax):
        X=itera
        print('iteramax superado, No converge')
    return(X,tabla)

def pivoteafila(A,B,vertabla=False):
    '''
    Pivotea parcial por filas, entrega matriz aumentada AB
    Si hay ceros en diagonal es matriz singular,
    Tarea: Revisar si diagonal tiene ceros
    '''
    A = np.array(A,dtype=float)
    B = np.array(B,dtype=float)
    # Matriz aumentada
    nB = len(np.shape(B))
    if nB == 1:
        B = np.transpose([B])
    AB  = np.concatenate((A,B),axis=1)
    
    if vertabla==True:
        print('Matriz aumentada')
        print(AB)
        print('Pivoteo parcial:')
    
    # Pivoteo por filas AB
    tamano = np.shape(AB)
    n = tamano[0]
    m = tamano[1]
    
    # Para cada fila en AB
    pivoteado = 0
    for i in range(0,n-1,1):
        # columna desde diagonal i en adelante
        columna = np.abs(AB[i:,i])
        dondemax = np.argmax(columna)
        
        # dondemax no es en diagonal
        if (dondemax != 0):
            # intercambia filas
            temporal = np.copy(AB[i,:])
            AB[i,:] = AB[dondemax+i,:]
            AB[dondemax+i,:] = temporal

            pivoteado = pivoteado + 1
            if vertabla==True:
                print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax+i)
    if vertabla==True:
        if pivoteado==0:
            print('  Pivoteo por filas NO requerido')
        else:
            print('AB')
    return(AB)

# PROGRAMA Búsqueda de solucion  --------


# PROCEDIMIENTO
AB = pivoteafila(A,B,vertabla=True)
# separa matriz aumentada en A y B
[n,m] = np.shape(AB)
A = AB[:,:m-1]
B = AB[:,m-1]

[X, puntos] = jacobi(A,B,X0,tolera,vertabla=True,precision=verdecimal)
iterado = len(puntos)

# numero de condicion
ncond = np.linalg.cond(A)

# SALIDA
print('numero de condición:', ncond)
print('respuesta X: ')
print(X)
print('iterado, incluyendo X0: ', iterado)

Ejercicio: 1Eva_2024PAOII_T2 Interpolar x(t) en caída de cofia para t entre[1,2]

De la tabla del ejercicio, solo se toman las dos primeras filas ti,xi

ti	1	1.2	1.4	1.8	2
xi	-80.0108	-45.9965	3.1946	69.5413	61.1849
yi	-8.3002	-22.6765	-20.9677	15.8771	33.8999
zi	113.8356	112.2475	110.5523	106.7938	104.71

literal a. Planteamiento

En el planteamiento del problema para un polinomio de grado 3 indicado en el enunciado, se requieren al menos 4 puntos (grado=puntos-1). Al requerir cubrir todo el intervalo, los puntos en los extremos son obligatorios, quedando solo dos puntos por seleccionar, que se sugiere usar alrededor de 1.63 que es el valor buscado. quedando de ésta forma la selección de los puntos:

xi = [1. , 1.4, 1.8, 2. ]
fi = [-80.0108, 3.1946,  69.5413,  61.1849]

En el parcial, se revisaron dos métodos: polinomio de interpolación con sistema de ecuaciones en la Unidad 3, y el conceptual con diferencias divididas de Newton. Por la extensión del desarrollo se realiza con diferencias divididas de Newton, que por facilidad de espacios se muestra en dos tablas, la de operaciones y resultados.

Tabla de operaciones:

i	ti	f[ti]	Primero	Segundo	Tercero
0	1	-80.0108	\frac{3.1946-(-80.0108)}{1.4-1}	\frac{165.8667-208.0135}{1.8-1}	\frac{-346.0812-52.6834}{2-1}
1	1.4	3.1946	\frac{69.5413-3.1946}{1.8-1.4}	\frac{-41.782-165.8667}{2-1.4}
2	1.8	69.5413	\frac{61.1849-69.5413}{2-1.8}
3	2	61.1849

Tabla de resultados

i	ti	f[ti]	Primero	Segundo	Tercero
0	1	-80.0108	208.0135	-52.6834	-293.3978
1	1.4	3.1946	165.8667	-346.0812
2	1.8	69.5413	-41.782
3	2	61.1849

Se construye el polinomio con los datos de la primera fila:

p(t) = -80.0108 +208.0135 (t - 1) - 52.6834(t - 1)(t - 1.4) -293.3978(t - 1)(t - 1.4)(t - 1.8)

literal b. verificar polinomio

Se puede verificar de dos formas: probando los puntos o con la gráfica del algoritmo. La forma de escritura del polinomio hace cero algunos términos.

p(1.4) = -80.0108+208.0135 ((1.4) - 1) - 52.6834((1.4) - 1)((1.4) - 1.4) -293.3978((1.4) - 1)((1.4) - 1.4)((1.4) - 1.8) = 3.1846 p(1.8) = -80.0108+208.0135 ((1.8) - 1) - 52.6834((1.8) - 1)(t - 1.4) -293.3978((1.8) - 1)((1.8) - 1.4)((1.8) - 1.8) =69.5413

La gráfica del algoritmo muestra que el polinomio pasa por todos los puntos.

literal c. error en polinomio

El punto de la tabla que no se usó es t = 1.2, que al evaluar en el polinomio se obtiene:

p(1.2) = -80.0108+ 208.0135 ((1.2) - 1) - 52.6834((1.2) - 1)((1.2) - 1.4) -293.3978((1.2) - 1)((1.2) - 1.4)((1.2) - 1.8) = -43.3423 errado = |-43.3423 -(-45.9965)| = 2.65

literal d. conclusiones y recomendaciones

Para el error  P(1.2). dado el orden de magnitud en el intervalo podría considerarse «bajo» e imperceptible al incorporarlo en la gráfica.

literal e. error en otro punto

El polinomio evaluado en t=1.65

p(1.65) = -80.0108 + 208.0135 ((1.65) - 1) - 52.6834((1.65) - 1)((1.65) - 1.4) -293.3978((1.65) - 1)((1.65) - 1.4)((1.65) - 1.8) = 53.7884

la fórmula para x(t) del tema 1

x(t) = 15.35 - 13.42 t+100e^{-0.12t} cos(2\pi (0.5) t + \pi / 8) x(1.65) = 15.35 - 13.42(1.65)+100e^{-0.12(1.65)} cos(2\pi (0.5) (1.65) + \pi / 8) = 55.5884 errado = |55.5884 -53.7884| = 1.79

resultados del algoritmo

Tabla Diferencia Dividida
[['i   ', 'xi  ', 'fi  ', 'F[1]', 'F[2]', 'F[3]', 'F[4]']]
[[   0.        1.      -80.0108  208.0135  -52.6834 -293.3978    0.    ]
 [   1.        1.4       3.1946  165.8667 -346.0812    0.        0.    ]
 [   2.        1.8      69.5413  -41.782     0.        0.        0.    ]
 [   3.        2.       61.1849    0.        0.        0.        0.    ]]
dDividida: 
[ 208.0135  -52.6834 -293.3978    0.    ]
polinomio: 
208.0135*t - 293.3978125*(t - 1.8)*(t - 1.4)*(t - 1.0) - 52.6834375000001*(t - 1.4)*(t - 1.0) - 288.0243
polinomio simplificado: 
-293.3978125*t**3 + 1179.587375*t**2 - 1343.7817375*t + 377.581375
>>> polinomio.subs(t,1.65)
53.7884880859375
>>> 15.35 - 13.42*(1.65)+100*np.exp(-0.12*(1.65))*np.cos(2*np.pi*(0.5)*(1.65) + np.pi/8)
55.588413032442766
>>> 55.5884 -53.7884
1.7999999999999972
>>>

las gráficas se muestran en los literales anteriores

# 1Eva_2024PAOII_T2 Interpolar x(t) en caída de cofia para t entre[1,2]
# Polinomio interpolación
# Diferencias Divididas de Newton
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO , Datos de prueba
xi = [1. , 1.4, 1.8, 2. ]
fi = [-80.0108, 3.1946,  69.5413,  61.1849]

##ti = [1. , 1.2, 1.4, 1.8, 2. ]
##xi = [-80.0108, -45.9965,   3.1946,  69.5413,  61.1849]
##yi = [ -8.3002, -22.6765, -20.9677,  15.8771,  33.8999]
##zi = [113.8356, 112.2475, 110.5523, 106.7938, 104.71 ]


# PROCEDIMIENTO
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)

# Tabla de Diferencias Divididas
titulo = ['i   ','xi  ','fi  ']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)

# diferencias divididas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)

# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
    # Añade título para cada columna
    titulo.append('F['+str(j-2)+']')

    # cada fila de columna
    i = 0
    paso = j-2 # inicia en 1
    while (i < diagonal):
        denominador = (xi[i+paso]-xi[i])
        numerador = tabla[i+1,j-1]-tabla[i,j-1]
        tabla[i,j] = numerador/denominador
        i = i+1
    diagonal = diagonal - 1
    j = j+1

# POLINOMIO con diferencias Divididas
# caso: puntos equidistantes en eje x
dDividida = tabla[0,3:]
n = len(dfinita)

# expresión del polinomio con Sympy
t = sym.Symbol('t')
polinomio = fi[0]
for j in range(1,n,1):
    factor = dDividida[j-1]
    termino = 1
    for k in range(0,j,1):
        termino = termino*(t-xi[k])
    polinomio = polinomio + termino*factor

# simplifica multiplicando entre (t-xi)
polisimple = polinomio.expand()

# polinomio para evaluacion numérica
px = sym.lambdify(t,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
np.set_printoptions(precision = 4)
print('Tabla Diferencia Dividida')
print([titulo])
print(tabla)
print('dDividida: ')
print(dDividida)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)

# Gráfica
plt.plot(xi,fi,'o', label = 'Puntos')
plt.plot(pxi,pfi, label = 'Polinomio')

plt.xlabel('ti')
plt.ylabel('xi')
plt.grid()
plt.title('Polinomio de interpolación')

plt.plot(1.65,polinomio.subs(t,1.65),
         'o',color='red',label='p(1.65)')
plt.plot(1.2,polinomio.subs(t,1.2),
         'o',color='green',label='p(1.2)')
plt.legend()
plt.show()

 

Ejercicio: 1Eva_2024PAOII_T1 Capturar en el mar las cofias de cohetes

literal a. Planteamiento

Para encontrar el valor t cuando la cofia alcanza 30 mts o 0.030 Km se usa la fórmula del eje z(t)=0.030 dado que se indica que las fórmulas se encuentran en Km.

z(t) = 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 0.030 = 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 f(t) = - 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 = 0

literal b, Intervalo para búsqueda

En el enunciado se indica que » trayectoria de caída que no es de más de 10 minutos desde desacople del cohete.»

Al considerar el inicio del «evento» desacople del cohete como t=0, el intervalo a usar es entre [0,10].

Para verificar el intervalo de búsqueda, se evalúa la función z(t) en los extremos del intervalo:

f(0) = - 0.030 + 120 + \frac{450}{60} (0) \Big(1-e^{-0.35(0)} \Big) - \frac{g}{2} (0)^2 + 0.012(7.5+25.28(0))^2 = 120.645 f(10) = - 0.030 + 120 + \frac{450}{60} (10) \Big(1-e^{-0.35(10)} \Big) - \frac{g}{2} (10)^2 + 0.012(7.5+g(10))^2 = -140.509

con lo que se muestra el cambio de signo de f(t) dentro del intervalo, que verifica el intervalo de búsqueda.

con el algoritmo:

>>> fz(0)-0.03
120.645
>>> fz(10)-0.03
-140.50972375667382
>>>

también puede verificarse usando las gráficas de las trayectorias de cada eje vs el tiempo en el intervalo. Para el eje z, se puede marcar el punto de interés al trazar una línea horizontal en cero o en la altura z(t) = 0.030.

literal c. Iteraciones

Se indica usar el método del punto fijo, donde es necesario definir g(t) como un lado de la balanza, mientra que del otro lado es la identidad con t. de la fórmula se despeja por ejemplo del término t²

\frac{g}{2} t^2 + 0.012(7.5+gt)^2 f(t) = - 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 = 0 \frac{g}{2} t^2 = - 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 t^2 = \frac{2}{g}\Big(- 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 \Big) t = \sqrt{\frac{2}{g} \Big(- 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 \Big)}

siendo g(t) la parte derecha de la ecuación:

g(t) = \sqrt{\frac{2}{g} \Big(- 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 \Big)}

el punto inicial t₀ se puede escoger por ejemplo la mitad del intervalo. Según se observa la gráfica.

La tolerancia puede ser de 10 cm, o 1 m, depende de la precisión a proponer.
Para la parte escrita se selecciona 1m, como las unidades se encuentran en Km: tolera = 0.001

itera = 0

t = 5

g(5) = \sqrt{\frac{2}{35.28} \Big(- 0.030 + 120 + \frac{450}{60} (5) \Big(1-e^{-0.35(5)} \Big) + 0.012(7.5+(35.28(5))^2 \Big)} g(5) = 5.28 error = |g(5)-5| = |5.28-5| = 0.28

que es mayor que la tolerancia.

itera = 0+1 = 1

itera = 1

t = 5.28

g(5.28) = \sqrt{\frac{2}{35.28} \Big(- 0.030 + 120 + \frac{450}{60} (5.28) \Big(1-e^{-0.35(5.28)} \Big) + 0.012(7.5+(35.28(5.28))^2 \Big)} g(5.28) = 5.51 error = |g(5.28)-5.28| = |5.51-5.28| = 0.23

que es mayor que la tolerancia.

itera = 1+1 = 2

itera = 2

t = 5.51

g(5.51) = \sqrt{\frac{2}{35.28} \Big(- 0.030 + 120 + \frac{450}{60} (5.51) \Big(1-e^{-0.35(5.51)} \Big) + 0.012(7.5+(35.28(5.51))^2 \Big)} g(5.51) = 5.70 error = |g(5.51)-5| = |5.70-5.51| = 0.19

que es mayor que la tolerancia.

literal d. tolerancia y error

La tolerancia se describe en la primera iteración. Por ejemplo tolera = 0.001, los errores se calculan en cada iteración.

literal e. Convergencia

El error se reduce en cada iteración, se considera que el método converge.

literal f. Respuestas con algoritmo

La respuesta de la raíz de la función se busca con el algoritmo, se requieren al menos 35 iteraciones en el método del punto fijo.

i,[a,b,tramo]
0 [5.     5.2881 0.2881]
1 [5.2881 5.5234 0.2353]
2 [5.5234 5.7176 0.1942]
3 [5.7176 5.8791 0.1615]
...
34 [6.7551e+00 6.7562e+00 1.1150e-03]
35 [6.7562e+00 6.7572e+00 9.5380e-04]
raíz en:  6.75719557313832
errado :  0.0009538025930524441
itera  :  3

la gráfica del intervalo muestra que es necesario ampliar(zoom) el eje f(x) para observar mejor.

Instrucciones en Python

# Algoritmo de punto fijo
# [a,b] son seleccionados desde la gráfica
# error = tolera

import numpy as np

# INGRESO
g = 35.28
alt =  0.030
fx = lambda t: -alt + 120 + 450/60*t*(1-np.exp(-0.35*t))-0.5*g*t**2 + 0.012*(7.5 - g*t)**2
gx = lambda t: np.sqrt((2/g)*(-alt + 120 + 450/60*t*(1-np.exp(-0.35*t)) + 0.012*(7.5 - g*t)**2))

a = 5
b = 10
tolera = 0.001 # tolera 1m, probar con 10 cm
iteramax = 100

# PROCEDIMIENTO
i = 0 # iteración
b = gx(a)
tramo = abs(b-a)

print('i,[a,b,tramo]')
np.set_printoptions(precision=4)
print(0,np.array([a,b,tramo]))

while not(tramo<=tolera or i>iteramax):
    a = b
    b = gx(a)
    tramo = abs(b-a)
    i = i + 1
    
    print(i,np.array([a,b,tramo]))

respuesta = b
# Valida convergencia
if (i>=iteramax):
    respuesta = np.nan

# SALIDA
print('raíz en: ', respuesta)
print('errado : ', tramo)
print('itera  : ', i)

# GRAFICA
import matplotlib.pyplot as plt
# calcula los puntos para fx y gx
a = 5
b = 10
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
gi = gx(xi)
yi = xi

plt.plot(xi,fi, label='f(t)',
         linestyle='dashed')
plt.plot(xi,gi, label='g(t)')
plt.plot(xi,yi, label='y=t')

plt.axvline(respuesta, color='magenta',
            linestyle='dotted')
plt.axhline(0)
plt.xlabel('t')
plt.ylabel('f(t)')
plt.title('Punto Fijo')
plt.grid()
plt.legend()
plt.show()

 

Ejercicio: 1Eva_2024PAOI_T3 Tasas de natalidad de reemplazo en Ecuador

Los datos de la tabla que se requieren usar para la tabla son los años 1965, 1980, 1995 y 2010.

Promedio Hijos por mujer en Ecuador. INEC 29 Agosto 2019 [4]

tasa	7.32	4.89	3.50	2.79
año	1965	1980	1995	2010
k	0	3	6	9

literal a

Para cuatro datos o muestras el grado del polinomio que se puede plantear es 3. La ecuación se ordena siguiendo el modelo para la matriz de Vandermonde, primer coeficiente es del termino de mayor grado.

p(x) = ax^3+bx^2+cx+d

Por el orden de magnitud del eje x comparado con los valores de las constantes, se usan los valores del vector k que corresponde a los índices de la tabla. El valor del año se obtiene al hacer un cambio de escala que inicia en el año t₀ = 1965 y tamaño de paso Δx = 5 años.

el sistema de ecuaciones usando cada punto será:

p(0) = a(0)^3+b(0)^2+c(0)+d = 7.32 p(3) = a(3)^3+b(3)^2+c(3)+d = 4.89 p(6) = a(6)^3+b(6)^2+c(6)+d = 3.50 p(9) = a(9)^3+b(9)^2+c(9)+d = 2.79

literal b

El sistema de ecuaciones para la Matriz de Vandermonde D y el vector de constantes B en la forma de matriz aumentada D|B:

\left[ \begin{array}{cccc | c} (0)^3 & (0)^2 & (0) & 1 & 7.32 \\ (3)^3 & (3)^2 & (3) &1 &4.89\\ (6)^3 & (6)^2 & (6) &1 & 3.50 \\ (9)^3 & (9)^2 & (9) & 1 & 2.79 \end{array} \right]

literal c

Resolviendo el sistema de ecuaciones con el algoritmo y usando la instrucción np.linalg.solve(A,B)

>>> np.linalg.solve(A,B)
array([-2.22222222e-03,  7.77777778e-02,
       -1.02333333e+00,  7.32000000e+00])

literal d

p(x) = -0.00222 x^3 + 0.07777 x^2 - 1.0233 x + 7.32

Para el ajuste de escala de años, se usa:

año = x*5 +1965

la gráfica usando el algoritmo, muestra que el polinomio pasa por los puntos seleccionados y existe un error entre los puntos que no participan en la construcción del polinomio.

literal e

El año 2020 en x se escala como

2020 = x*5 +1965

x = 11

o revisando la tabla proporcionada en el ejercicio

p(11) = -0.00222 (11)^3 + 0.07777(11)^2 - 1.0233 (11)x + 7.32 = 2.5166

el error se calcula usando el valor medido para el año 2020

error = | 2.51- 2.35| = 0.16

literal f

p(x) = -0.00222 x^3 + 0.07777 x^2 - 1.0233 x + 7.32 = 2.51

para resolverlo se requiere usar cualquiera de los algoritmos de la unidad 2.

>>> import scipy.optimize as opt
>>> opt.bisect(px,11,30,xtol=0.001)
20.312713623046875
>>>

que corresponde al año = 20.31*5+1965 = 2066.55

Sin embargo la interpolación se usa para estimar valores dentro del intervalo de muestras. El concepto de extrapolación corresponde a otro capítulo. Sin embargo la pregunta se la considera para evaluar la comprensión de la unidad 2.

---

Algoritmo con Python

El resultado con el algoritmo se observa como

xi [0 3 6 9]
fi [7.32 4.89 3.5  2.79]
Matriz Vandermonde: 
[[  0.   0.   0.   1.]
 [ 27.   9.   3.   1.]
 [216.  36.   6.   1.]
 [729.  81.   9.   1.]]
los coeficientes del polinomio: 
[-2.22222222e-03  7.77777778e-02 
 -1.02333333e+00  7.32000000e+00]
Polinomio de interpolación: 
-0.00222222224*x**3 + 0.077777778*x**2 - 1.02333333*x + 7.32

 formato pprint
                       3                      2                            
- 0.002222222224*x  + 0.0777777778*x  - 1.023333333*x + 7.32
>>> px(11)
2.5166666666667066

Instrucciones en Python

# 1Eva_2024PAOI_T3 Tasas de natalidad en países desarrollados
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym

# INGRESO
tasa = [7.32, 6.39, 5.58, 4.89,4.31,3.85,3.50,3.26,3.03,2.79,2.54,2.35]
anio = [1965, 1970, 1975, 1980,1985,1990,1995,2000,2005,2010,2015,2020]
k    = [   0,     1,   2,    3,   4,   5,   6,   7,   8,   9,  10,  11]
cual = [0,3,6,9]
tasamin = 2.1

# PROCEDIMIENTO
fi = np.take(tasa,cual)
xi = np.take(k,cual)

# El polinomio de interpolación
# muestras = tramos+1
muestras = 25

# PROCEDIMIENTO
# Convierte a arreglos numpy 
xi = np.array(xi)
B = np.array(fi)
n = len(xi)

# Matriz Vandermonde D
D = np.zeros(shape=(n,n),dtype =float)
for i in range(0,n,1):
    for j in range(0,n,1):
        potencia = (n-1)-j # Derecha a izquierda
        D[i,j] = xi[i]**potencia

# Aplicar métodos Unidad03. Tarea
# Resuelve sistema de ecuaciones A.X=B
coeficiente = np.linalg.solve(D,B)

# Polinomio en forma simbólica
x = sym.Symbol('x')
polinomio = 0
for i in range(0,n,1):
    potencia = (n-1)-i   # Derecha a izquierda
    termino = coeficiente[i]*(x**potencia)
    polinomio = polinomio + termino

# Polinomio a forma Lambda
# para evaluación con vectores de datos xin
px = sym.lambdify(x,polinomio)

# Para graficar el polinomio en [a,b]
a = np.min(xi)
b = np.max(xi)
xin = np.linspace(a,b,muestras)
yin = px(xin)
   
# SALIDA
print('xi', xi)
print('fi',fi)
print('Matriz Vandermonde: ')
print(D)
print('los coeficientes del polinomio: ')
print(coeficiente)
print('Polinomio de interpolación: ')
print(polinomio)
print('\n formato pprint')
sym.pprint(polinomio)

# Grafica
plt.plot(anio,tasa,'o')
plt.plot(xi*5+anio[0],fi,'o',color='red', label='[xi,fi]')
plt.plot(xin*5+anio[0],yin,color='red', label='p(x)')
plt.xlabel('xi')
plt.ylabel('fi')
plt.legend()
plt.axhline(0)
plt.axhline(2.1,linestyle='-.')
plt.xlabel('anio')
plt.ylabel('tasa')
plt.title(polinomio)
plt.show()

 

Ejercicio: 1Eva_2024PAOI_T2 Temperatura en nodos de placa cuadrada

literal a

El planteamiento de las ecuaciones según se cita en la solución iterativa es el promedio de los nodos adyacentes:

 

a = \frac{100+40+b+c}{4} b = \frac{40+20+a+d}{4} c = \frac{100+80+a+d}{4} d = \frac{80+20+c+b}{4}

reordenando las ecuaciones para su forma maticial:

4a -b -c = 100+40 4b -a -d= 40+20 4c -a -d= 100+80 4d -c -b= 80+20

literal b

la forma matricial del sistema de ecuaciones es:

\begin{bmatrix} 4 & -1 &-1 & 0 \\ -1 & 4 & 0 &-1 \\ -1 & 0 & 4 &-1 \\ 0 & -1 &-1 & 4 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} = \begin{bmatrix} 140 \\ 60 \\ 180 \\ 100 \end{bmatrix}

matriz aumentada:

\left[ \begin{array} {cccc|c} 4 & -1 &-1 & 0 & 140\\ -1 & 4 & 0 &-1 & 60 \\ -1 & 0 & 4 &-1 & 180 \\ 0 & -1 &-1 & 4 & 100 \end{array}\right]

al revisar el procedimiento de pivoteo parcial por filas se muestra que ya se encuentra pivoteada la matriz. Por lo que no es necesario realizar cambios en las filas.

literal c

Las expresiones a partir de la matriz aumentada y pivoteada para usar en un método iterativo como Gauss-Seidel son:

a = 0.25(b+c+140) b = 0.25*(a+d+60) c = 0.25(a+d+180) d = 0.25(c+b+100)

el vector inicial debe considerar que las temperaturas serán medias entre los  bordes de la placa

X₀ = [ (100+40)/2, (40+20)/2, (100+80)/2, (80+20)/2 ]

X₀ = [ 70, 30, 90, 50 ]

literal d iteraciones

itera = 0

a = 0.25(30+90+140)= 65

b = 0.25*(65+50+60) = 43.75

c = 0.25(65+50+180) = 73.75

d = 0.25(73.75+43.75+100) = 54.375

error = max|[65-70, 43.75-30, 73.75-90, 54.375-50]|

error = max|[ -5, 13.75, -16.25, 4.375| = 16.25

X₁ = [ 65, 43.75, 73.75, 54.375 ]

itera = 1

a = 0.25(43.75+73.75+140)= 64.375

b = 0.25*(64.375+54.375+60) = 44.687

c = 0.25(64.375+54.375+180) = 74.687

d = 0.25(74.687+44.687+100) = 54.843

error = max|[64.375-65, 44.687-43.75, 74.687-73.75, 54.843-54.375]|

error = max|[-0.625, 0.937, 0.937, 0.468| = 0.937

X₂ = [ 64.375, 44.687, 74.687, 54.843 ]

itera = 2

a = 0.25(44.687+74.687+140)= 64.843

b = 0.25*(64.843 +54.843+60) = 44.921

c = 0.25(64.843+54.843+180) = 74.921

d = 0.25(74.921+44.921+100) = 54.960

error = max|[64.843-64.375, 44.921-44.687, 74.921-74.687, 54.960-54.843]|

error = max|[0.468, 0.234, 0.234, 0.117| = 0.468

X₃ = [ 64.843, 44.921, 74.921, 54.960 ]

literal e

El método converge pues los errores en cada iteración disminuyen. Los valores obtenidos en el resultado son acorde a las temperaturas esperadas en los nodos.

Algoritmos con Python

Los resultados obtenidos son:

X 0 = [65.    43.75  73.75  54.375]
X 1 = [64.375   44.6875  74.6875  54.84375]
X 2 = [64.84375   44.921875  74.921875  54.9609375]
X 3 = [64.9609375  44.98046875 74.98046875 54.99023438]
X 4 = [64.99023438 44.99511719 74.99511719 54.99755859]
X 5 = [64.99755859 44.9987793  74.9987793  54.99938965]
X 6 = [64.99938965 44.99969482 74.99969482 54.99984741]
X 7 = [64.99984741 44.99992371 74.99992371 54.99996185]
X 8 = [64.99996185 44.99998093 74.99998093 54.99999046]
X 9 = [64.99999046 44.99999523 74.99999523 54.99999762]
respuesta X: 
[[64.99999046]
 [44.99999523]
 [74.99999523]
 [54.99999762]]
verificar A.X=B: 
[[139.99997139]
 [ 59.99999285]
 [179.99999285]
 [100.        ]]
>>>

el algoritmo usado es:

# 1Eva_2024PAOI_T2 Temperatura en nodos de placa cuadrada
# Método de Gauss-Seidel
import numpy as np
# INGRESO
A = np.array([[4,-1,-1,0],
              [-1,4,0,-1],
              [-1,0,4,-1],
              [0,-1,-1,4]],dtype=float)
B = np.array([140,60,180,100],dtype=float)
X0  = np.array([70,30,90,50],dtype=float)

tolera = 0.0001
iteramax = 100

# PROCEDIMIENTO
# Gauss-Seidel
tamano = np.shape(A)
n = tamano[0]
m = tamano[1]
#  valores iniciales
X = np.copy(X0)
diferencia = np.ones(n, dtype=float)
errado = 2*tolera

itera = 0
while not(errado<=tolera or itera>iteramax):
    # por fila
    for i in range(0,n,1):
        # por columna
        suma = 0 
        for j in range(0,m,1):
            # excepto diagonal de A
            if (i!=j): 
                suma = suma-A[i,j]*X[j]
        nuevo = (B[i]+suma)/A[i,i]
        diferencia[i] = np.abs(nuevo-X[i])
        X[i] = nuevo
    print('X',itera,'=',X)
    errado = np.max(diferencia)
    itera = itera + 1

# Respuesta X en columna
X = np.transpose([X])
# revisa si NO converge
if (itera>iteramax):
    X=0
# revisa respuesta
verifica = np.dot(A,X)

# SALIDA
print('respuesta X: ')
print(X)
print('verificar A.X=B: ')
print(verifica)

 

Ejercicio: 1Eva_2024PAOI_T1 Vaciado de reservorio semiesférico

literal a. Planteamiento

A partir de la solución expresión propuesta y simplificada del ejercicio, se reemplaza los valores de R, K, a y g que son constantes. Como se da el valor de t=(15 min)(60 s/min), se unifica la unidad de medida de tiempo a segundos pues g=9.6 m/s².

---

-\frac{4}{3}R h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{Ka}{\pi} t \sqrt{2g}

---

-\frac{4}{3}(3) h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{(0.85)(0.01)}{\pi} (15)(60) \sqrt{2(9.8)}

la función para encontrar la raíz se reordena como f(h)=0

f(h) = -\frac{4}{3}(3) h^{3/2} + \frac{2}{5} h^{5/2} +\frac{(0.85)(0.01)}{\pi} (15)(60) \sqrt{2(9.8)} f(h) = -4h^{3/2} + 0.4 h^{5/2} +10.7805

Usando la gráfica proporcionada del reservorio semiesférico, el valor de h no puede superar la altura R. Al vaciar el reservorio h=0.

Por lo que el intervalo a usar es [0,3]. Se verifica la existencia de una raíz al con la gráfica y Python.

b. Método de Newton Raphson

El método requiere la derivada f'(h)

f(h) = -4h^{3/2} + 0.4 h^{5/2} +10.7805 f'(h) = -6\frac{ h^{3/2}}{h} + \frac{h^{5/2}}{h} f'(h) = -6 h^{1/2}+ h^{3/2}

El valor inicial puede ser por ejemplo, el centro del intervalo:

x_0= \frac{a+b}{2} = \frac{0+3}{2} = 1.5

itera=0

f(1.5) = -4(1.5)^{3/2} + 0.4 (1.5)^{5/2} +10.7805= 4.5343 f'(1.5) = -6\frac{ 1.5^{3/2}}{1.5} + \frac{1.5^{5/2}}{1.5} = -5.5113 x_1= x_0 - \frac{f(1.5)}{f'(1.5)}= 1.5-\frac{4.5343}{-5.5113} =2.3227 error_1 =|x1-x0| = |2.3227-1.5| =0.8227

itera=1

f(2.3227) = -4(2.3227)^{3/2} + 0.4 (2.3227)^{5/2} +10.7805= -0.09019 f'(2.3227) = -6\frac{ 2.3227^{3/2}}{2.3227} + \frac{2.3227^{5/2}}{2.3227} = -5.6043 x_2= 2.3227-\frac{-0.09019}{-5.6043} = 2.3066 error_2 = |2.3066-2.3227| =0.01611

itera=2

f(2.3227) = -4(2.3066)^{3/2} + 0.4 (2.3066)^{5/2} +10.7805= -0.0007104 f'(2.3227) = -6\frac{ 2.3227^{3/2}}{2.3227} + \frac{2.3227^{5/2}}{2.3227} = -5.6093 x_3= 2.3227-\frac{-0.0007104}{-5.6093} = 2.3066 error_3 = |2.3066-2.3066| =0.000007241

literal c, convergencia

considerando tolerancia de 10-3 (milimétrica), solo serán necesarias 3 iteraciones.

El método converge al mostrarse que los errores disminuyen en cada iteración.

El resultado se encuentra dentro del intervalo y es x = 2.3066

Algoritmo con Python

resultados:

fh:
         ____          ____                   
        /  3          /  5                    
- 4.0*\/  h   + 0.4*\/  h   + 10.7805172327811
dfh:
         ____          ____
        /  3          /  5 
  6.0*\/  h     1.0*\/  h  
- ----------- + -----------
       h             h     
['xi', 'xnuevo', 'tramo']
[[1.5000e+00 2.3227e+00 8.2272e-01]
 [2.3227e+00 2.3066e+00 1.6118e-02]
 [2.3066e+00 2.3066e+00 7.2412e-06]]
raiz en:  2.306612665792577
con error de:  7.241218404896443e-06

>>> f(1.5)
4.534318388683996
>>> df(1.5)
-5.5113519212621505
>>> f(2.3227)
-0.09019959114247378
>>> df(2.3227)
-5.604354799446854
>>> f(2.3066)
7.104683901282272e-05
>>> df(2.3066)
-5.609349350102558

instrucciones:

# 1Eva_2024PAOI_T1 Vaciado de reservorio semiesférico
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym

# INGRESO
h = sym.Symbol('h')
t = 15*60
R = 3 
g = 9.8 
area = 0.01
K = 0.85 
fh = -(4/3)*R*sym.sqrt(h**3)+(2/5)*sym.sqrt(h**5)+(K*area/np.pi)*np.sqrt(2*g)*(t)

# Grafica de f(h)
a = 0
b = 3
muestras = 15

# PROCEDIMIENTO
hi = np.linspace(a,b,muestras)
# para evaluación numérica con numpy
f = sym.lambdify(h,fh)
fi = f(hi)

# derivada con sympy
dfh = sym.diff(fh,h,1)
df = sym.lambdify(h,dfh)

# SALIDA
print('fh:')
sym.pprint(fh)
print('dfh:')
sym.pprint(dfh)

plt.plot(hi,fi)
plt.axhline(0, color='black')
plt.xlabel('h')
plt.ylabel('f')
plt.title(fh)
plt.show()

## Método de Newton-Raphson

# INGRESO
fx  = f
dfx = df
x0 = (a+b)/2 # mitad del intervalo (ejemplo)
tolera = 0.001

# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# SALIDA
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)

 

ejercicio: 1Eva_2023PAOI_T3 Recoger los restos de sumergible

literal a

Para realizar el planteamiento del ejercicio, se realiza la gráfica para observar mejor los puntos.

Se podría observar los puntos y plantear un primer recorrido como el siguiente

los puntos corresponden a los índices j = [0 ,2, 5, 6, 11]:

# INGRESO
xj = np.array([0.2478, 0.6316, 1.3802, 2.4744, 2.7351, 2.8008,
               3.5830, 3.6627, 3.7213, 4.2796, 4.3757, 4.6794])
fj = np.array([1.8108, 0.1993, 4.7199, 2.4529, 2.3644, 3.5955,
               2.6558, 4.3657, 4.1932, 4.6998, 4.7536, 1.5673])

# selecionando puntos
j = [0, 2, 5, 6, 11]
xi = xj[j]
fi = fj[j]

literal b

Partiendo del algoritmo de Diferencias divididas de Newton, y añadiendo vectores xj y fj para todos los puntos dados en el ejercicio.

Tabla Diferencia Dividida
[['i   ', 'xi  ', 'fi  ', 'F[1]', 'F[2]', 'F[3]', 'F[4]', 'F[5]']]
[[ 0.      0.2478  1.8108  2.569  -1.3163  0.3389 -0.0561  0.    ]
 [ 1.      1.3802  4.7199 -0.7915 -0.1861  0.09    0.      0.    ]
 [ 2.      2.8008  3.5955 -1.2014  0.111   0.      0.      0.    ]
 [ 3.      3.583   2.6558 -0.9928  0.      0.      0.      0.    ]
 [ 4.      4.6794  1.5673  0.      0.      0.      0.      0.    ]]
dDividida: 
[ 2.569  -1.3163  0.3389 -0.0561  0.    ]
polinomio: 
2.56896856234546*x - 0.0561488275125463*(x - 3.583)*(x - 2.8008)*(x - 1.3802)*(x - 0.2478) 
+ 0.338875729488637*(x - 2.8008)*(x - 1.3802)*(x - 0.2478) 
- 1.31628089036375*(x - 1.3802)*(x - 0.2478) + 1.17420959025079
polinomio simplificado: 
-0.0561488275125463*x**4 + 0.788728905753656*x**3 
- 3.98331084054791*x**2 + 7.41286537452727*x 
+ 0.206696844067185
>>>

usando la tabla de diferencias divididas se plantea la expresión para el polinomio:

p(x) = 1.8108 + 2.569 (x-0.2478) + + (-1.3163)(x-0.2478)(x-1.3802) + + 0.3389 (x-0.2478)(x-1.3802)(x-2.8008) + + (-0.0561)(x-0.2478)(x-1.3802)(x-2.8008)(x-3.583)

el algoritmo simplifica la expresión al siguiente polinomio,

p(x) = -0.0561 x^4 + 0.7887 x^3 - 3.9833 x^2 + 7.4128 x + 0.2066

literal c

Se usa el algoritmo Interpolación polinómica de Lagrange con Python para desarrollar el polinomio a partir de los puntos no usados en el literal anterior.

j = [3,4,7,8,9,10]

Para evitar oscilaciones grandes, se excluye el punto con índice 1, y se obtiene una opción mostrada:

con el siguiente resultado:

    valores de fi:  [2.4529 2.3644 4.3657 4.1932 4.6998 4.7536]
divisores en L(i):  [-1.32578996  0.60430667 -0.02841115  0.02632723 -0.09228243  0.13986517]

Polinomio de Lagrange, expresiones
-1.85014223337671*(x - 4.3757)*(x - 4.2796)*(x - 3.7213)*(x - 3.6627)*(x - 2.7351) 
+ 3.9125829809921*(x - 4.3757)*(x - 4.2796)*(x - 3.7213)*(x - 3.6627)*(x - 2.4744) 
- 153.661523787291*(x - 4.3757)*(x - 4.2796)*(x - 3.7213)*(x - 2.7351)*(x - 2.4744) 
+ 159.272361555669*(x - 4.3757)*(x - 4.2796)*(x - 3.6627)*(x - 2.7351)*(x - 2.4744) 
- 50.928437685792*(x - 4.3757)*(x - 3.7213)*(x - 3.6627)*(x - 2.7351)*(x - 2.4744) 
+ 33.9870187307222*(x - 4.2796)*(x - 3.7213)*(x - 3.6627)*(x - 2.7351)*(x - 2.4744)

Polinomio de Lagrange: 
-9.26814043907703*x**5 + 163.708008152209*x**4 
- 1143.16428460497*x**3 + 3941.13583467614*x**2 
- 6701.74628786718*x + 4496.64364271972
>>> 

Para presentar la parte analítica puede seleccionar menos puntos, se busca mostrar la aplicación del algoritmo, no necesariamente cuan largo puede ser.

p(x) = + 2.4529\frac{(x - 4.3757)(x - 4.2796)(x - 3.7213)(x - 3.6627)(x - 2.7351) }{(2.4744 - 4.3757)(2.4744 - 4.2796)(2.4744 - 3.7213)(2.4744 - 3.6627)(2.4744 - 2.7351)} + 2.3644\frac{ (x - 4.3757)(x - 4.2796)(x - 3.7213)(x - 3.6627)(x - 2.4744) }{(2.7351 - 4.3757)(2.7351 - 4.2796)(2.7351 - 3.7213)(2.7351 - 3.6627)(2.7351 - 2.4744)} +4.3657\frac{(x - 4.3757)(x - 4.2796)(x - 3.7213)(x - 2.7351)(x - 2.4744) }{(3.6627 - 4.3757)(3.6627 - 4.2796)(3.6627 - 3.7213)(3.6627 - 2.7351)(3.6627 - 2.4744)} + 4.1932 \frac{(x - 4.3757)(x - 4.2796)(x - 3.6627)(x - 2.7351)(x - 2.4744) }{(3.7213 - 4.3757)(3.7213 - 4.2796)(3.7213 - 3.6627)(3.7213 - 2.7351)(3.7213 - 2.4744)} +4.6998\frac{(x - 4.3757)(x - 3.7213)(x - 3.6627)(x - 2.7351)(x - 2.4744) }{(4.2796 - 4.3757)(4.2796 - 3.7213)(4.2796 - 3.6627)(4.2796 - 2.7351)(4.2796 - 2.4744)} + 4.7536 \frac{(x - 4.2796)(x - 3.7213)(x - 3.6627)(x - 2.7351)(x - 2.4744)}{(4.3757 - 4.2796)(4.3757 - 3.7213)(4.3757 - 3.6627)(4.3757 - 2.7351)(4.3757 - 2.4744)}

literal d

las gráficas se han presentado en el planteamiento para justificar los criterios usados.

literal e

Los errores de encuentran como la diferencia de los puntos no usados en el polinomio, y evaluando el polinomio en cada coordenada x.

Como las propuestas de polinomio pueden ser variadas se obtendrán diferentes respuestas para cada literal.

Se revisa la aplicación de conceptos en las propuestas.

 

Algoritmos usados

literal b. Diferencias divididas de Newton

# 1Eva_2023PAOI_T3 Recoger los restos de sumergible
# Polinomio interpolación
# Diferencias Divididas de Newton
# Tarea: Verificar tamaño de vectores,
#        verificar puntos equidistantes en x
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
xj = np.array([0.2478, 0.6316, 1.3802, 2.4744, 2.7351, 2.8008,
               3.5830, 3.6627, 3.7213, 4.2796, 4.3757, 4.6794])
fj = np.array([1.8108, 0.1993, 4.7199, 2.4529, 2.3644, 3.5955,
               2.6558, 4.3657, 4.1932, 4.6998, 4.7536, 1.5673])

# selecionando puntos
j = [0, 2, 5, 6, 11]
xi = xj[j]
fi = fj[j]


# PROCEDIMIENTO

# Tabla de Diferencias Divididas Avanzadas
titulo = ['i   ','xi  ','fi  ']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)

# diferencias divididas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)

# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
    # Añade título para cada columna
    titulo.append('F['+str(j-2)+']')

    # cada fila de columna
    i = 0
    paso = j-2 # inicia en 1
    while (i < diagonal):
        denominador = (xi[i+paso]-xi[i])
        numerador = tabla[i+1,j-1]-tabla[i,j-1]
        tabla[i,j] = numerador/denominador
        i = i+1
    diagonal = diagonal - 1
    j = j+1

# POLINOMIO con diferencias Divididas
# caso: puntos equidistantes en eje x
dDividida = tabla[0,3:]
n = len(dfinita)

# expresión del polinomio con Sympy
x = sym.Symbol('x')
polinomio = fi[0]
for j in range(1,n,1):
    factor = dDividida[j-1]
    termino = 1
    for k in range(0,j,1):
        termino = termino*(x-xi[k])
    polinomio = polinomio + termino*factor

# simplifica multiplicando entre (x-xi)
polisimple = polinomio.expand()

# polinomio para evaluacion numérica
px = sym.lambdify(x,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
np.set_printoptions(precision = 4)
print('Tabla Diferencia Dividida')
print([titulo])
print(tabla)
print('dDividida: ')
print(dDividida)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)

# Gráfica
plt.plot(xj,fj,'o',color='red')
plt.plot(xi,fi,'o', label = 'Puntos')
##for i in range(0,n,1):
##    plt.axvline(xi[i],ls='--', color='yellow')

plt.plot(pxi,pfi, label = 'Polinomio')
plt.legend()
plt.grid()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Diferencias Divididas - Newton')
plt.show()

literal c. Polinomio de Lagrange

# 1Eva_2023PAOI_T3 Recoger los restos de sumergible
# Interpolacion de Lagrange
# divisoresL solo para mostrar valores
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO , Datos de prueba
xj = np.array([0.2478, 0.6316, 1.3802, 2.4744, 2.7351, 2.8008,
               3.5830, 3.6627, 3.7213, 4.2796, 4.3757, 4.6794])
fj = np.array([1.8108, 0.1993, 4.7199, 2.4529, 2.3644, 3.5955,
               2.6558, 4.3657, 4.1932, 4.6998, 4.7536, 1.5673])

# selecionando puntos
#j = [0, 2, 5, 6, 11]
j = [3,4,7,8,9,10]
xi = xj[j]
fi = fj[j]

# PROCEDIMIENTO
# Polinomio de Lagrange
n = len(xi)
x = sym.Symbol('x')
polinomio = 0
divisorL = np.zeros(n, dtype = float)
for i in range(0,n,1):
    
    # Termino de Lagrange
    numerador = 1
    denominador = 1
    for j  in range(0,n,1):
        if (j!=i):
            numerador = numerador*(x-xi[j])
            denominador = denominador*(xi[i]-xi[j])
    terminoLi = numerador/denominador

    polinomio = polinomio + terminoLi*fi[i]
    divisorL[i] = denominador

# simplifica el polinomio
polisimple = polinomio.expand()

# para evaluación numérica
px = sym.lambdify(x,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
print('    valores de fi: ',fi)
print('divisores en L(i): ',divisorL)
print()
print('Polinomio de Lagrange, expresiones')
print(polinomio)
print()
print('Polinomio de Lagrange: ')
print(polisimple)

# Gráfica
plt.plot(xj,fj,'o',color='red')
plt.plot(xi,fi,'o', label = 'Puntos')
plt.plot(pxi,pfi, label = 'Polinomio')
plt.legend()
plt.grid()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Interpolación Lagrange')
plt.show()

 

Ejercicio: 1Eva_2023PAOI_T2 Productos en combo por subida de precio

literal a

Para el ejercicio solo es posible plantear tres ecuaciones, se muestran datos solo para tres semanas. Se tienen 4 incógnitas, por lo que tendría infinitas soluciones y no se podría resolver.

500 a + 600 b + 400 c + 90 d = 1660 800 a + 450 b + 300 c + 100 d = 1825 400 a + 300 b + 600 c + 80 d = 1430

Sin embargo desde el punto de vista práctico se puede usar una variable libre, considerando algunos criterios como:

– que en la nota se da el precio para la docena de huevos a 2.5 USD
– que la variable para huevos es la de menor cantidad se puede incurrir en un menor error si el precio ha variado en los últimos días respecto a lo que se podría haber tenido como referencia.

500 a + 600 b + 400 c = 1660 - 90 d 800 a + 450 b + 300 c = 1825 - 100 d 400 a + 300 b + 600 c = 1430 - 80 d

que al sustituir con d = 2.5

500 a + 600 b + 400 c = 1660 - 90 (2.5) =1435 800 a + 450 b + 300 c = 1825 - 100 (2.5) = 1575 400 a + 300 b + 600 c = 1430 - 80 (2.5) = 1230

Nota: el estudiante puede realizar una justificación diferente para el uso de otra variable libre.

literal b

La forma matricial del sistema de ecuaciones se convierte a:

\begin{pmatrix} 500 & 600 & 400 & \Big| & 1435 \\ 800 & 450 & 300 & \Big| & 1575 \\ 400 & 300 & 600 &\Big| & 1230 \end{pmatrix}

literal c

pivoteando la matriz aumentada, se encuentra que para la primera columna se pivotean la fila 1 y 2, por ser 800 el valor de mayor magnitud:

\begin{pmatrix} 800 & 450 & 300 & \Big| & 1575 \\ 500 & 600 & 400 & \Big| & 1435 \\ 400 & 300 & 600 &\Big| & 1230 \end{pmatrix}

luego, observando la segunda columna desde el elemento de la diagonal hacia abajo, se observa que el mayor valor en magnitud ya se encuentra en la diagonal. No se requieren intercambios de fila para la tercera columna.

literal d

Para el método iterativo de Gauss-Seidel se requiere el vector inicial, tomando las observaciones de la nota. Se da un precio de 50 USD por un quintal métrico de 100Kg, por lo que se estima que el precio por kilogramo ronda 50/100= 0.5 USD. Se indica además que los demás valores se encuentran en el mismo orden de magnitud, por lo que se tiene como vector inicial

X₀ = [0.5, 0.5, 0.5]

Para un método iterativo se despejan las ecuaciones como:

a = \frac {1575 - 450 b - 300 c}{800} b = \frac {1435 -500 a - 400 c}{600} c = \frac {1230 - 400 a - 300 b}{600}

Para el cálculo del error se considera que se busca un precio, lo regular es considerar el centavo, es decir una tolerancia 10^-2. Para el desarrollo se considera usar cuatro decimales por si se considera truncar o redondear.

itera = 0

a = \frac {1575 - 450 (0.5) - 300 (0.5)}{800} = 1.5 b = \frac {1435 -500(1.5) - 400 (0.5)}{600} = 0.8083 c = \frac {1230 - 400(1.5) - 300 (0.8083)}{600} =0.6458

errado = max|[1.5-0.5, 0.8083-0.5, 0.6458-0.5]|
errado = max|[1, 0.3083, 0.1458]| = 1

itera = 1

X₁ = [1.5, 0.8083, 0.6458]

a = \frac {1575 - 450 (0.8083) - 300 (0.6458)}{800} = 1.2719 b = \frac {1435 -500(1.2719) - 400 (0.6458)}{600} = 0.9012 c = \frac {1230 - 400 (1.2719) - 300 (0.9012)}{600} = 0.7514

errado = max|[1.2719-1.5, 0.9012-0.8083, 0.7514-0.6458]|
errado = max|[-0.2281, 0.0929, 0.1056]| = 0.2281

el error disminuye entre iteraciones.

itera = 2

X₂ = [1.2719 , 0.9012, 0.7514]

a = \frac {1575 - 450 (0.9012) - 300 (0.7514)}{800} = 1.1805 b = \frac {1435 -500 (1.1805) - 400 (0.7514)}{600} = 0.9069 c = \frac {1230 - 400 (1.1805) - 300 (0.9069)}{600} = 0.8095

errado = max|[ 1.1805-1.2719 , 0.9069-0.9012, 0.8095-0.7514]|
errado = max|[-0.0914, 0.0057, 0.1056]| = 0.1056

el error disminuye entre iteraciones.

literal e

Si el error entre iteraciones disminuye, se considera que el método converge.

usando el algoritmo Método de Gauss-Seidel con Python, se tiene como resultado en 13 iteraciones:

[1.5        0.80833333 0.64583333] 1.0
[1.271875   0.90121528 0.75147569] 0.2281249999999999
[1.18001302 0.90733869 0.80965531] 0.09186197916666661
[1.15475125 0.88960375 0.83536396] 0.025708648304880177
[1.1550864  0.87218536 0.84384972] 0.01741839593330019
[1.16170209 0.86101511 0.84502438] 0.011170246538965367
[1.16754486 0.85536303 0.84395525] 0.005842764350612484
[1.17112508 0.85309227 0.84270381] 0.0035802211655899807
[1.17287167 0.85247107 0.84185002] 0.0017465903731879173
[1.17354127 0.85248226 0.84139802] 0.0006695985845832642
[1.17370447 0.85264759 0.84120656] 0.00019146597344232852
[1.17368327 0.8527929  0.84114804] 0.00014530950399282982
[1.17362348 0.85288174 0.84114348] 8.884049018109685e-05
respuesta X: 
[[1.17362348]
 [0.85288174]
 [0.84114348]]
verificar A.X=B: 
[[1575.03861029]
 [1434.99817609]
 [1230.        ]]
iteraciones 13
>>> 

instrucciones en Python

Se debe recordar que las matrices y vectores deben ser tipo real (float) .

# Método de Gauss-Seidel
# solución de sistemas de ecuaciones
# por métodos iterativos

import numpy as np

# INGRESO
A = np.array([[800, 450, 300],
              [500, 600, 400],
              [400, 300, 600]], dtype=float)

B = np.array([1575, 1435,1230], dtype=float)

X0  = np.array([0.5,0.5,0.5])

tolera = 0.0001
iteramax = 100

# PROCEDIMIENTO

# Gauss-Seidel
tamano = np.shape(A)
n = tamano[0]
m = tamano[1]
#  valores iniciales
X = np.copy(X0)
diferencia = np.ones(n, dtype=float)
errado = 2*tolera

itera = 0
while not(errado<=tolera or itera>iteramax):
    # por fila
    for i in range(0,n,1):
        # por columna
        suma = 0 
        for j in range(0,m,1):
            # excepto diagonal de A
            if (i!=j): 
                suma = suma-A[i,j]*X[j]
        
        nuevo = (B[i]+suma)/A[i,i]
        diferencia[i] = np.abs(nuevo-X[i])
        X[i] = nuevo
    errado = np.max(diferencia)
    print(X,errado)
    itera = itera + 1

# Respuesta X en columna
X = np.transpose([X])

# revisa si NO converge
if (itera>iteramax):
    X=0
# revisa respuesta
verifica = np.dot(A,X)

# SALIDA
print('respuesta X: ')
print(X)
print('verificar A.X=B: ')
print(verifica)
print('iteraciones',itera)