Ejercicio: 2Eva_IT2010_T3 EDP elíptica, Placa no rectangular
la fórmula a resolver, siendo f(x,y)=20
\frac{\delta^2 u}{\delta x^2} + \frac{\delta^2 u}{\delta y^2} = f
\frac{\delta^2 u}{\delta x^2} + \frac{\delta^2 u}{\delta y^2} = 20
Siendo las condiciones de frontera en los bordes marcados:
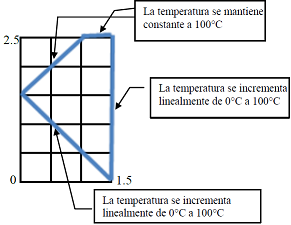
Se convierte a forma discreta la ecuación
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{\Delta x^2} + \frac{u_{i,j+1} -2u_{i,j}+u_{i,j-1}}{\Delta y^2} = 20
u_{i+1,j}-2u_{i,j}+u_{i-1,j} + \frac{\Delta x^2}{\Delta y^2} \Big( u_{i,j+1} -2u_{i,j}+u_{i,j-1} \Big) = 20 \Delta x^2
siendo λ = 1, al tener la malla en cuadrícula Δx=Δy
u_{i+1,j}-4u_{i,j}+u_{i-1,j} + u_{i,j+1}+u_{i,j-1} = 20 \Delta x^2
despejando u[i,j]
u_{i,j} =\frac{1}{4}\Big(u_{i+1,j}+u_{i-1,j} + u_{i,j+1}+u_{i,j-1} - 20 \Delta x^2 \Big)
Para el ejercicio, se debe usar las fronteras para los valores de cálculo que se puede hacer de dos formas:
1. Por posición del valor en la malla [i,j]
2. Por valor xi,yj que es la forma usada cuando la función es contínua.
1. Por posición del valor en la malla
Se busca la posición de la esquina derecha ubicada en xi = 0 y yj=1.5 y se la ubica como variable 'desde' como referencia para ubicar los valores de las fronteras usando los índices i, j.
# valores en fronteras
# busca poscición de esquina izquierda
desde = -1
for j in range(0,m,1):
if ((yj[j]-1.5)<tolera):
desde = j
# llena los datos de bordes de placa
for j in range(0,m,1):
if (yj[j]>=1):
u[j-desde,j] = Ta
u[n-1,j] = Tb(xi[n-1],yj[j])
for i in range(0,n,1):
if (xi[i]>=1):
u[i,m-1]=Td
u[i,desde-i] = Tc(xi[i],yj[i])
# valor inicial de iteración
2. Por valor xi, yj
Se establecen las ecuaciones que forman la frontera:
ymin = lambda x,y: 1.5-(1.5/1.5)*x
ymax = lambda x,y: 1.5+(1/1)*x
que se usan como condición para hacer el cálculo en cada nodo
if ((yj[j]-yjmin)>tolera and (yj[j]-yjmax)<-tolera):
u[i,j] = (u[i-1,j]+u[i+1,j]+u[i,j-1]+u[i,j+1]-20*(dx**2))/4
Para minimizar errores por redondeo o truncamiento al seleccionar los puntos, la referencia hacia cero se toma como "tolerancia"; en lugar de más que cero o menos que cero.
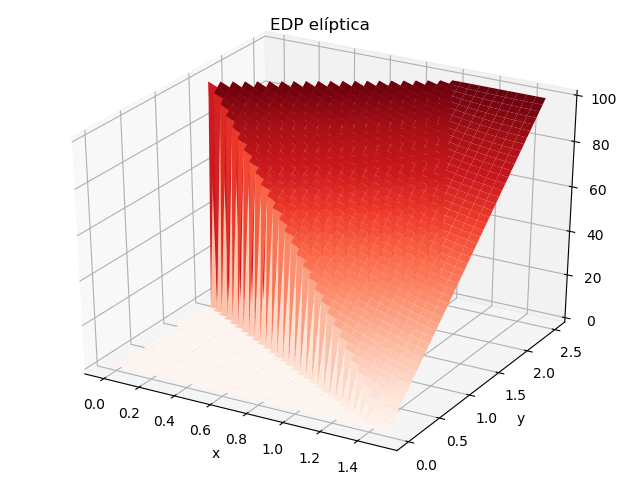
Con lo que se obtiene el resultado mostrado en la gráfica aumentando la resolución con Δx=Δy=0.05:
converge = 1
xi=
[0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65
0.7 0.75 0.8 0.85 0.9 0.95 1. 1.05 1.1 1.15 1.2 1.25 1.3 1.35
1.4 1.45 1.5 ]
yj=
[0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65
0.7 0.75 0.8 0.85 0.9 0.95 1. 1.05 1.1 1.15 1.2 1.25 1.3 1.35
1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2. 2.05
2.1 2.15 2.2 2.25 2.3 2.35 2.4 2.45 2.5 ]
matriz u
[[ 0. 0. 0. ... 0. 0. 0. ]
[ 0. 0. 0. ... 0. 0. 0. ]
[ 0. 0. 0. ... 0. 0. 0. ]
...
[ 0. 0. 6.67 ... 96.1 98.03 100. ]
[ 0. 3.33 5.31 ... 96.03 98. 100. ]
[ 0. 2. 4. ... 96. 98. 100. ]]
>>>
Algoritmo en Python
# Ecuaciones Diferenciales Parciales
# Elipticas. Método iterativo para placa NO rectangular
import numpy as np
# INGRESO
# Condiciones iniciales en los bordes
Ta = 100
Tb = lambda x,y:(100/2.5)*y
Tc = lambda x,y: 100-(100/1.5)*x
Td = 100
# dimensiones de la placa no rectangular
x0 = 0
xn = 1.5
y0 = 0
yn = 2.5
ymin = lambda x,y: 1.5-(1.5/1.5)*x
ymax = lambda x,y: 1.5+(1/1)*x
# discretiza, supone dx=dy
dx = 0.05
dy = 0.05
maxitera = 100
tolera = 0.0001
# PROCEDIMIENTO
xi = np.arange(x0,xn+dx,dx)
yj = np.arange(y0,yn+dy,dy)
n = len(xi)
m = len(yj)
# Matriz u
u = np.zeros(shape=(n,m),dtype = float)
# valores en fronteras
# busca posición de esquina izquierda
desde = -1
for j in range(0,m,1):
if ((yj[j]-1.5)<tolera): desde = j
# llena los datos de bordes de placa
for j in range(0,m,1): if (yj[j]>=1):
u[j-desde,j] = Ta
u[n-1,j] = Tb(xi[n-1],yj[j])
for i in range(0,n,1):
if (xi[i]>=1):
u[i,m-1]=Td
u[i,desde-i] = Tc(xi[i],yj[i])
# valor inicial de iteración
# se usan los valores cero
# iterar puntos interiores
itera = 0
converge = 0
while not(itera>=maxitera and converge==1):
itera = itera + 10000
nueva = np.copy(u)
for i in range(1,n-1):
for j in range(1,m-1):
yjmin = ymin(xi[i],yj[j])
yjmax = ymax(xi[i],yj[j])
if ((yj[j]-yjmin)>tolera and (yj[j]-yjmax)<-tolera):
u[i,j] = (u[i-1,j]+u[i+1,j]+u[i,j-1]+u[i,j+1]-20*(dx**2))/4
diferencia = nueva-u
erroru = np.linalg.norm(np.abs(diferencia))
if (erroru<tolera):
converge=1
# SALIDA
np.set_printoptions(precision=2)
print('converge = ', converge)
print('xi=')
print(xi)
print('yj=')
print(yj)
print('matriz u')
print(u)
Para incorporar la gráfica en forma de superficie.
# Gráfica
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
X, Y = np.meshgrid(xi, yj)
U = np.transpose(u) # ajuste de índices fila es x
figura = plt.figure()
ax = Axes3D(figura)
ax.plot_surface(X, Y, U, rstride=1, cstride=1, cmap=cm.Reds)
plt.title('EDP elíptica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()