Referencia: Chapra 17.1 p 466. Burden 8.1 p498
Cuando los datos de un experimento presentan variaciones o errores sustanciales respecto al modelo matemático, la interpolación polinomial presentada en la Unidad 4 es inapropiada para predecir valores intermedios.
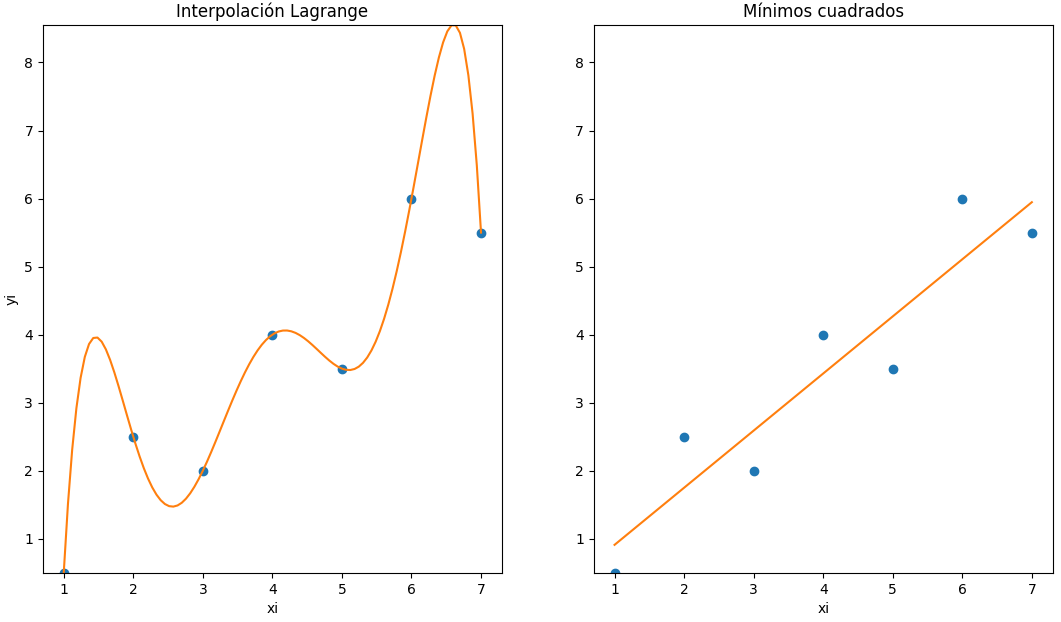
En el ejemplo de Chapra 17.1 p470, se presentan los datos de un experimento mostrados en la imagen y la siguiente tabla:
xi = [1, 2, 3, 4, 5, 6, 7] yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5]
Un polinomio de interpolación, por ejemplo de Lagrange de grado 6 pasará por todos los puntos, pero oscilando.
Una función de aproximación que se ajuste a la tendencia general, que no necesariamente pasa por los puntos de muestra puede ser una mejor respuesta. Se busca una "curva" que minimice las diferencias entre los puntos y la curva, llamada regresión por mínimos cuadrados.
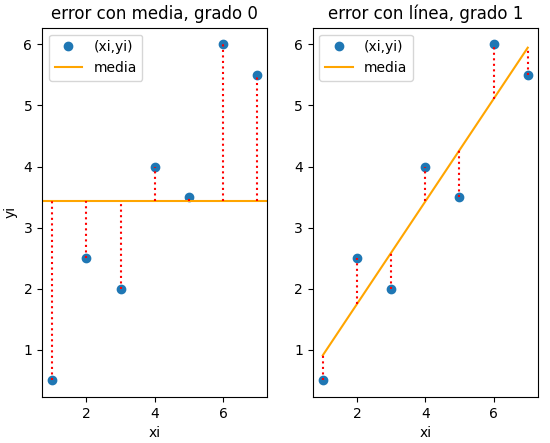
Descripción con la media yi
Considere una aproximación para la relación entre los puntos xi, yi como un polinomio, grado 0 que sería la media de yi. Para este caso, los errores se presentan en la gráfica:
Otra forma sería aproximar el comportamiento de los datos es usar un polinomio de grado 1. En la gráfica se pueden observar que para los mismos puntos el error disminuye considerablemente.
El polinomio de grado 1 recibe el nombre de regresión por mínimos cuadrados, que se desarrolla en la siguiente sección.
Instrucciones Python
# representación con la media import numpy as np import matplotlib.pyplot as plt # INGRESO xi = [1, 2, 3, 4, 5, 6, 7] yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5] # PROCEDIMIENTO xi = np.array(xi,dtype=float) yi = np.array(yi,dtype=float) n = len(xi) xm = np.mean(xi) ym = np.mean(yi) # SALIDA print('ymedia = ', ym) # grafica plt.plot(xi,yi,'o',label='(xi,yi)') plt.stem(xi,yi,bottom=ym, linefmt = '--') plt.xlabel('xi') plt.ylabel('yi') plt.legend() plt.show()
Instrucciones Python - compara interpolación y regresión.
Para ilustrar el asunto y para comparar los resultados se usa Python, tanto para interpolación y mínimos cuadrados usando las librerías disponibles. Luego se desarrolla el algoritmo paso a paso.
# mínimos cuadrados import numpy as np import scipy.interpolate as sci import matplotlib.pyplot as plt # INGRESO xi = [1, 2, 3, 4, 5, 6, 7] yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5] # PROCEDIMIENTO xi = np.array(xi) yi = np.array(yi) n = len(xi) # polinomio Lagrange px = sci.lagrange(xi,yi) xj = np.linspace(min(xi),max(xi),100) pj = px(xj) # mínimos cuadrados A = np.vstack([xi, np.ones(n)]).T [m0, b0] = np.linalg.lstsq(A, yi, rcond=None)[0] fx = lambda x: m0*(x)+b0 fi = fx(xi) # ajusta límites ymin = np.min([np.min(pj),np.min(fi)]) ymax = np.max([np.max(pj),np.max(fi)]) # SALIDA plt.subplot(121) plt.plot(xi,yi,'o',label='(xi,yi)') plt.plot(xj,pj,label='P(x) Lagrange') plt.ylim(ymin,ymax) plt.xlabel('xi') plt.ylabel('yi') plt.title('Interpolación Lagrange') plt.subplot(122) plt.plot(xi,yi,'o',label='(xi,yi)') plt.plot(xi,fi,label='f(x)') plt.ylim(ymin,ymax) plt.xlabel('xi') plt.title('Mínimos cuadrados') plt.show()