[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
..
Referencia: Chapra 11.2 p310, Burden 7.3 p337, Rodríguez 5.2 p162
El método de Gauss-Seidel, reescribe las expresiones del sistema de ecuaciones, despejando la incógnita de la diagonal en cada ecuación. Usa el vector inicial X0, actualizando el vector X por cada nuevo valor calculado del vector. La diferencia principal con el método de Jacobi es la actualización de X en cada cálculo, por lo que las iteraciones llegan más rápido al punto cuando el método converge.
Las iteraciones pueden ser o no, convergentes.
La expresión para encontrar nuevos valores usando la matriz de coeficientes A, el vector de constantes B y como incógnitas X es la misma que Jacobi:
x_i = \bigg(b_i - \sum_{j=0, j\neq i}^n a_{i,j}x_j\bigg) \frac{1}{a_{ii}}La convergencia del método iterativo se puede revisar usando el número de condición de la matriz de coeficientes A. Un resultado cercano a 1, implica que el sistema será convergente.
cond(A) = ||A|| ||A-1||
np.linalg.cond(A)
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
..
2. Ejercicio
Referencia: 1Eva_IIT2011_T2 Sistema de Ecuaciones, diagonal dominante
Considere el siguiente sistema de ecuaciones AX=B dado por:
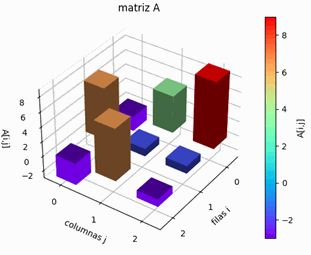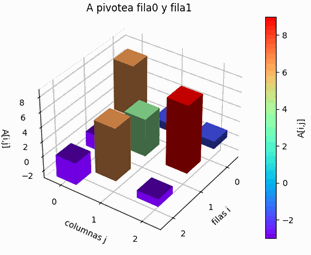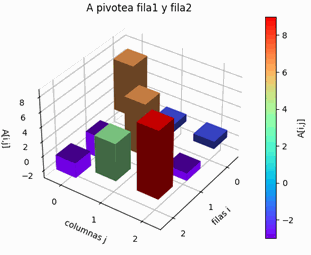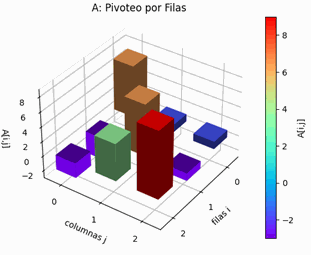
\begin{cases} -2x+5y+9z=1\\7x+y+z=6\\-3x+7y-z=-26\end{cases}Luego del pivoteo parcial por filas, el sistema de ecuaciones a usar para el método de Gauss-Seidel es:
\begin{cases} 7x+y+z=6\\-3x+7y-z=-26\\-2x+5y+9z=1\end{cases}Desarrolle el ejercicio usando el método de Gauss-Seidel, tomando como vector inicial X0=[0,0,0] y tolerancia de 0.0001
Compare los resultados con el método de Jacobi.
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
..
3. Desarrollo Analítico
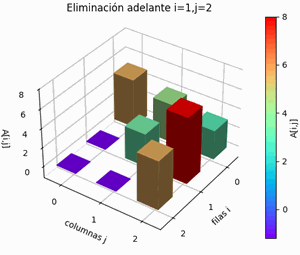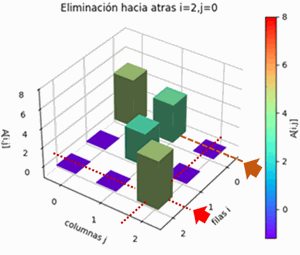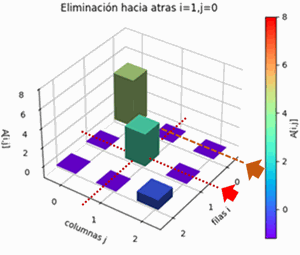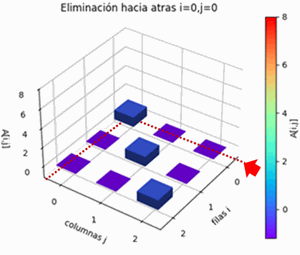
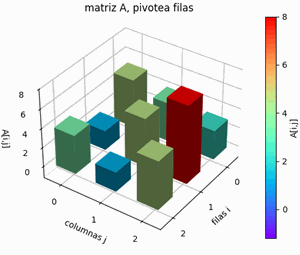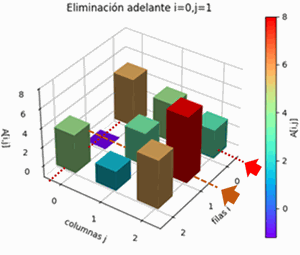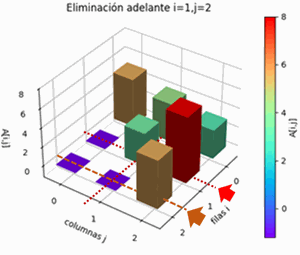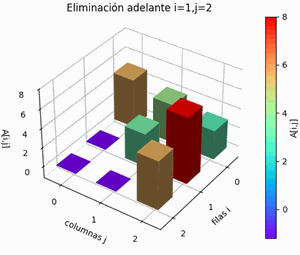
Para el método de Gauss-Seidel, se usan las ecuaciones reordenas con el pivoteo parcial por filas, para que en lo posible sea diagonal dominante que mejora la convergencia. El resultado del algoritmo a partir de las ecuaciones presentadas al inicio es:
Pivoteo parcial por filas AB: [[ 7. 1. 1. 6.] [ -3. 7. -1. -26.] [ -2. 5. 9. 1.]] A: [[ 7. 1. 1.] [-3. 7. -1.] [-2. 5. 9.]] B: [ 6. -26. 1.]\begin{cases} 7x+y+z=6\\-3x+7y-z=-26\\-2x+5y+9z=1\end{cases}
se reescriben despejando la incógnita de la diagonal en cada ecuación.
x=\frac{6-y-z}{7} y= \frac{-26+3x+z}{7} z=\frac{1+2x-5y}{9}El vector inicial X0=[0,0,0] representa un punto de partida, valores estimados o semilla para buscar la solución a las variables X0=[x0,y0,z0].
Como las ecuaciones son el comportamiento del 'sistema', se usan con X0 para obtener un nuevo y mejor valor estimado para la solución.
itera = 0
X_0=[x_0,y_0,z_0] X_1 = X_0=[0,0,0] x_1=\frac{6-(0)-(0)}{7} =\frac{6}{7}=0.8571Se actualiza el vector X1,
X_1 = [0.8571,0,0] y_1= \frac{-26+3(0.8571)+(0)}{7} =-3.3469Se actualiza el vector X1,
X_1 = [0.8571,-3.3469,0] z_1=\frac{1+2(0.8571)-5(-3.3469)}{9} =\frac{1}{9}=2.161 X_1=[0.8571, -3.3469, 2.161]Para revisar si se está más cerca o no de la solución se calculan los desplazamientos o diferencias entre los valores anteriores y los nuevos:
\text{diferencias}=X_1-X_0 =[0.8571-0, -3.3469-0, 2.161-0][0.8571, -3.3469, 2.161] -[0. , 0. , 0. ] __________________________ [0.8571, -3.3469, 2.161]\text{diferencias}=[0.8571, -3.3469, 2.161]
Para estimar el valor del error, se presenta un valor simplificado o escalar de las diferencias (norma del error). Por simplicidad se usa el valor de magnitud máxima. Se usa como variable 'errado', para evitar el conflicto de nombre de variable error usada como palabra reservada en Python:
\text{errado}= max \Big|\text{diferencias}\Big| \text{errado}= max \Big|[0.8571, -3.3469, 2.161]\Big| = 3.3469Al comparar el valor errado con la tolerancia, se observa que el error aún es mayor que lo tolerado. Por lo que se sigue con la siguiente iteración.
itera = 1
X_1=[x_1,y_1,z_1] X_2 = X_1=[0.8571, -3.3469, 2.161] x_2=\frac{6-(-3.3469)-(2.161)}{7} = 1.0266Se actualiza el vector X2,
X_2 = [1.0266, -3.3469, 2.161] y_2= \frac{-26+3(1.0266)+(2.161)}{7} =-2.9656Se actualiza el vector X2,
X_2 = [1.0266, -2.9656, 2.161] z_2=\frac{1+2(1.0266)-5(-2.9656)}{9} =1.9868 X_2 = [1.0266, -2.9656, 1.9868] \text{diferencias}=|X_2-X_1| =|[1.0266-0.8571, -2.9656-(-3.3469), 1.9868-2.161]|[1.0266, -2.9656, 1.9868] -[0.8571, -3.3469, 2.161 ] __________________________ [0.1694, 0.3813, 0.1742]\text{diferencias}= |[0.1694, 0.3813, 0.1742]| \text{errado}=max |X_2-X_1|= 0.3813
itera = 2
X_3 = X_2=[1.0266, -2.9656, 1.9868] x_3=\frac{6-(-2.9656)-(1.9868)}{7} = 0.997 X_3 =[0.997, -2.9656, 1.9868] y_3= \frac{-26+3(0.997)+(1.9868)}{7} = -3.0032 X_3 =[0.997, -3.0032, 1.9868] z_3=\frac{1+2(0.997)-5(-3.0032)}{9} = 2.0011 X_3 =[0.997, -3.0032, 2.0011] \text{diferencias}=|X_3-X_2| =|[0.997-1.0266, -3.0032-(-2.9656), 2.0011-1.9868]|[ 0.997 , -3.0032, 2.0011] -[ 1.0266, -2.9656, 1.9868] __________________________ [-0.0296, 0.0376, 0.0143]\text{diferencias}=|[-0.0296, 0.0376, 0.0143]| \text{errado}=max |X_2-X_1|= 0.0376
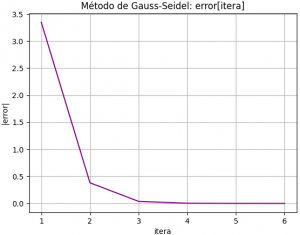En cada iteración el valor de error disminuye, por lo que se estima que el método converge.
Al usar el algoritmo, de los resultados se observa que se detiene luego de 6 iteraciones, los errores son menores a la tolerancia:
Iteraciones Gauss-Seidel itera,[X] errado,[diferencia] 0 [0. 0. 0.] 0.0002 1 [ 0.8571 -3.3469 2.161 ] 3.3469387755102042 [0.8571 3.3469 2.161 ] 2 [ 1.0266 -2.9656 1.9868] 0.381322597066037 [0.1694 0.3813 0.1742] 3 [ 0.997 -3.0032 2.0011] 0.03756644188210334 [0.0296 0.0376 0.0143] 4 [ 1.0003 -2.9997 1.9999] 0.00346691102194141 [0.0033 0.0035 0.0012] 5 [ 1. -3. 2.] 0.0003256615309844557 [3.2566e-04 3.0918e-04 9.9398e-05] 6 [ 1. -3. 2.] 2.996898191776065e-05 [2.9969e-05 2.7044e-05 8.3644e-06] Metodo de Gauss-Seidel numero de condición: 1.9508402675105447 X: [ 1. -3. 2.] errado: 2.996898191776065e-05 iteraciones: 6
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
..
4. Algoritmo en Python
El algoritmo para Gauss-Seidel es semejante al realizado para Jacobi, se debe incorporar las instrucciones para actualizar los valores de X[i] en cada uso de ecuación o fila.
Para el algoritmo se usa el sistema de ecuaciones en su forma matricial A.X=B.
Se asume que se ha aplicado el pivoteo parcial por filas y matriz aumentada.
i=0 # una ecuacion suma = B[i] # numerador for j in range(0,m,1): # un coeficiente if (i!=j): # excepto diagonal de A suma = suma-A[i,j]*X[j] nuevo = suma/A[i,i] diferencia[i] = abs(nuevo-X[i]) X[i] = nuevo errado = np.max(diferencia)
La actualización para el algoritmo es:
# Método de Gauss-Seidel import numpy as np # INGRESO # NOTA: Para AB, se ha usado pivoteo parcial por filas A = [[ 7, 1, 1], [-3, 7, -1], [-2, 5, 9]] B = [6, -26, 1] X0 = [0,0,0] tolera = 0.0001 iteramax = 100 # PROCEDIMIENTO # Matrices como arreglo, numeros reales A = np.array(A,dtype=float) B = np.array(B,dtype=float) X0 = np.array(X0,dtype=float) tamano = np.shape(A) # tamaño A n = tamano[0] m = tamano[1] # valores iniciales diferencia = np.ones(n, dtype=float) errado = 2*tolera # np.max(diferencia) itera = 0 X = np.copy(X0) while errado>tolera and itera<=iteramax: for i in range(0,n,1): # una ecuacion suma = B[i] # numerador for j in range(0,m,1): # un coeficiente if (i!=j): # excepto diagonal de A suma = suma-A[i,j]*X[j] nuevo = suma/A[i,i] diferencia[i] = abs(nuevo-X[i]) X[i] = nuevo errado = np.max(diferencia) print(itera, X) print(' ',errado,diferencia) itera = itera + 1 if (itera>iteramax): # No converge X = np.nan print('No converge,iteramax superado') # numero de condicion ncond = np.linalg.cond(A) # SALIDA print('Método de Gauss-Seidel') print('numero de condición:', ncond) print('X: ',X) print('errado:',errado) print('iteraciones:', itera)
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
..
5. Algoritmo en Python como función
Las instrucciones del algoritmo, empaquetadas como función, añaden algunas facilidades para el desarrollo del ejercicio. Antes de usar el método de Gauss-Seidel, se aplica el pivoteo parcial por filas para mejorar de ser posible la convergencia.
En la función gauss_seidel() se añaden las instrucciones para mostrar los resultados parciales en cada iteración. Se añade una tabla para revisión de valores al final del algoritmo, o para realizar la gráfica de errores por iteración.
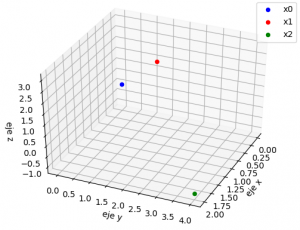
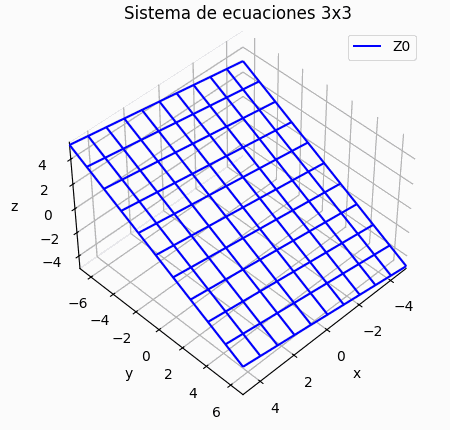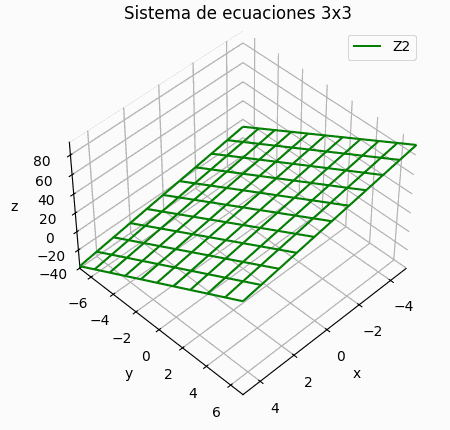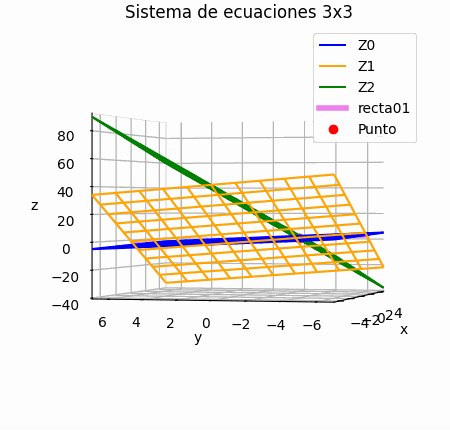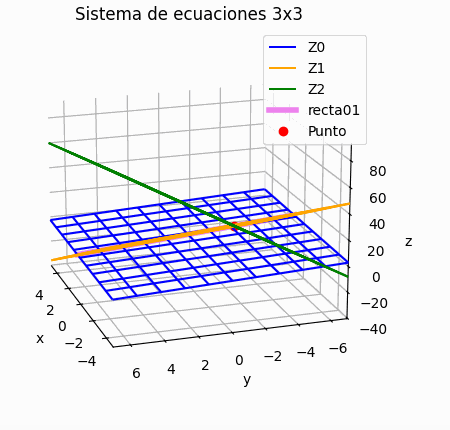
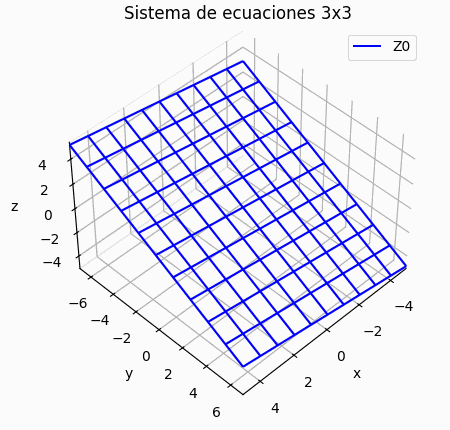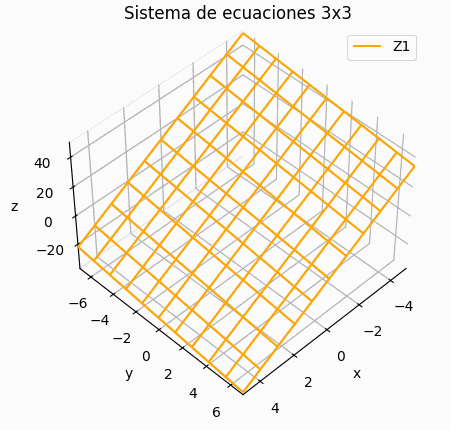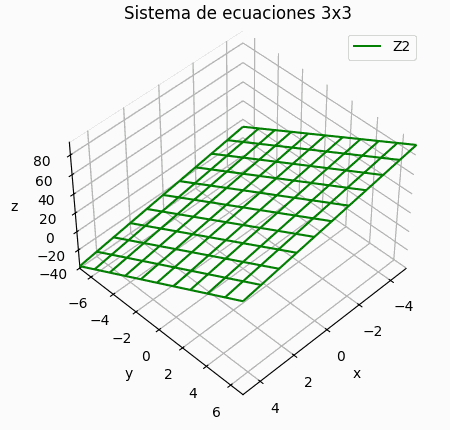
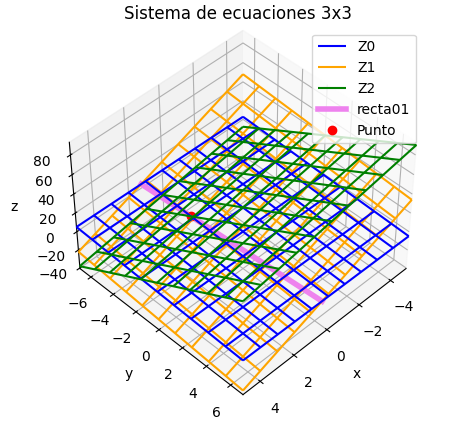
Si el sistema es de 3x3 se puede añadir una gráfica de los resultados por iteración, mostrando la trayectoria descrita por los resultados parciales en 3D.
# Algoritmo Gauss-Seidel # solución de matrices # métodos iterativos # Referencia: Chapra 11.2, p.310, # Rodriguez 5.2 p.162 import numpy as np def gauss_seidel(A,B,X0,tolera, iteramax=100, vertabla=False, precision=4): ''' Método de Gauss Seidel, tolerancia, vector inicial X0 para mostrar iteraciones: vertabla=True ''' # Matrices como arreglo, numeros reales A = np.array(A, dtype=float) B = np.array(B, dtype=float) X0 = np.array(X0, dtype=float) tamano = np.shape(A) n = tamano[0] m = tamano[1] # valores iniciales diferencia = 2*tolera*np.ones(n, dtype=float) errado = 2*tolera # np.max(diferencia) tabla = [np.copy(X0)] # tabla de iteraciones tabla = np.concatenate((tabla,[[np.nan]]), axis=1) # añade errado if vertabla==True: print('Iteraciones Gauss-Seidel') print('itera,[X]') print(' errado,[diferencia]') print(0,X0) print(' ',np.nan) np.set_printoptions(precision) itera = 0 # Gauss-Sediel X = np.copy(X0) while (errado>tolera and itera<iteramax): for i in range(0,n,1): # una ecuacion suma = B[i] for j in range(0,m,1): if (i!=j): suma = suma-A[i,j]*X[j] nuevo = suma/A[i,i] diferencia[i] = np.abs(nuevo-X[i]) X[i] = nuevo errado = np.max(diferencia) Xfila= np.concatenate((X,[errado]),axis=0) tabla = np.concatenate((tabla,[Xfila]),axis = 0) itera = itera + 1 if vertabla==True: print(itera, X) print(' ', errado,diferencia) # No converge if (itera>iteramax): X = np.nan print('No converge,iteramax superado') return(X,tabla) def pivoteafila(A,B,vertabla=False): ''' Pivotea parcial por filas, entrega matriz aumentada AB Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) if vertabla==True: print('Matriz aumentada') print(AB) print('Pivoteo parcial:') # Pivoteo por filas AB tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax+i) if vertabla==True: if pivoteado==0: print(' Pivoteo por filas NO requerido') else: print('AB') print(AB) return(AB) # PROGRAMA Búsqueda de solucion -------- # INGRESO A = [[ 7, 1, 1], [-3, 7, -1], [-2, 5, 9]] B = [6, -26, 1] X0 = [0,0,0] tolera = 0.0001 iteramax = 100 verdecimal = 4 # PROCEDIMIENTO AB = pivoteafila(A,B,vertabla=True) n,m = np.shape(AB) A = AB[:,:n] # separa en A y B B = AB[:,n] [X, tabla] = gauss_seidel(A,B,X0, tolera, vertabla=True, precision=verdecimal) n_itera = len(tabla)-1 errado = tabla[-1,-1] # numero de condicion ncond = np.linalg.cond(A) # SALIDA print('Metodo de Gauss-Seidel') print('numero de condición:', ncond) print('X: ',X) print('errado:',errado) print('iteraciones:', n_itera)
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
..
4.1 Gráficas de iteraciones
Se muestra la gráfica de errores vs iteraciones.
# GRAFICA de iteraciones errados = tabla[:,n] import matplotlib.pyplot as plt # grafica de error por iteracion fig2D = plt.figure() graf = fig2D.add_subplot(111) graf.plot(errados,color='purple') graf.set_xlabel('itera') graf.set_ylabel('|error|') graf.set_title('Método de Gauss-Seidel: error[itera]') graf.grid() plt.show()
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
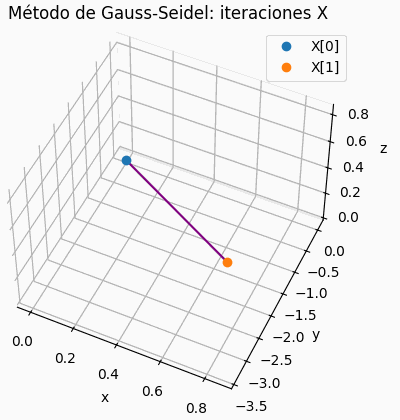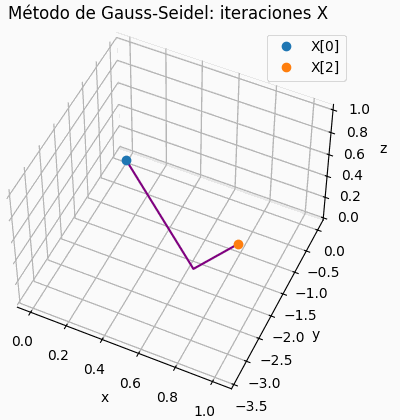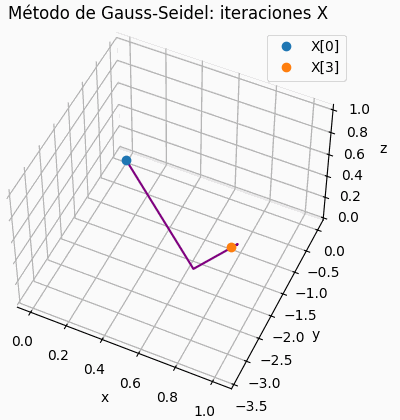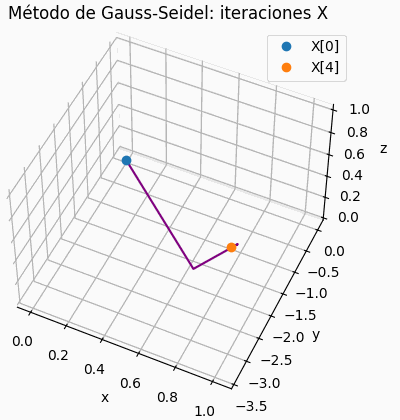
4.2 Gráfica de iteraciones para sistema de 3×3
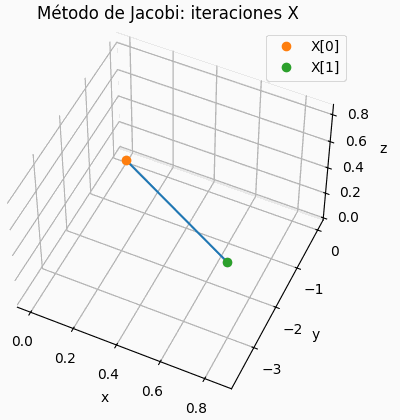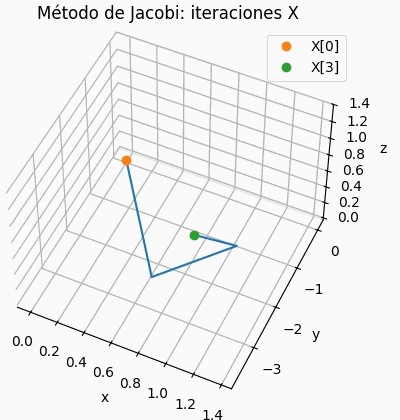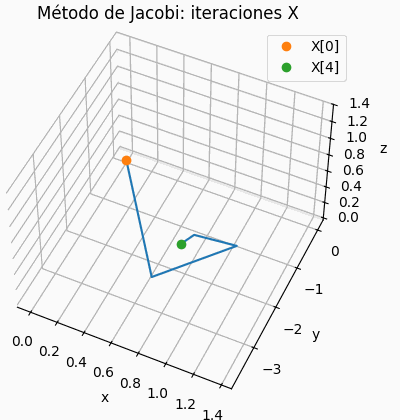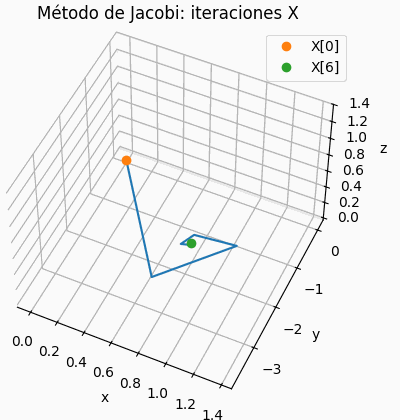
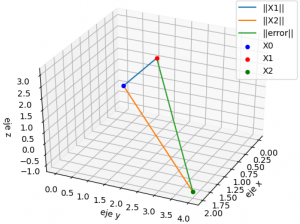
Si el sistema es de 3×3, se muestra una gráfica de la trayectoria de resultados parciales, semejante a la presentada para la descripción del concepto. Permite observar si la espiral es convergente o no.
# grafica de iteraciones x,y,z # solo para 3x3 xp = tabla[:,0] yp = tabla[:,1] zp = tabla[:,2] fig3D = plt.figure() graf3D = fig3D.add_subplot(111,projection='3d') graf3D.plot(xp,yp,zp,color='purple') graf3D.plot(xp[0],yp[0],zp[0],'o',label='X[0]') graf3D.plot(xp[n_itera],yp[n_itera],zp[n_itera], 'o',label='X['+str(n_itera)+']') graf3D.set_xlabel('x') graf3D.set_ylabel('y') graf3D.set_zlabel('z') graf3D.set_title('Método de Gauss-Seidel: iteraciones X') # graf3D.view_init(45,45) plt.legend() plt.show()
[ Gauss-Seidel ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ] [Gráfica]
