Referencia: Chapra 10.3.1 p298 pdf322, Burden 9Ed Cap7.1 p432, Rodriguez 4.4.1 p132
Normas de un vector en 3D
La norma de un vector se interpreta como una distancia entre la coordenada definida por el vector [xi, yi, zi] y el origen [0,0,0]. También se puede realizar respecto a otro punto de referencia, se conoce como Norma Ecuclidiana o Norma p=2.
Previamente, en busqueda de raíces, el error de aproximación se considera como la diferencia entre dos iteraciones sucesivas:.
error = |x_{i+1} - x_{i}|Si el concepto se extiende a vectores en tres dimensiones, se observa como el error entre vectores |Xi+1 – Xi| que se interpreta mejor como una distancia.
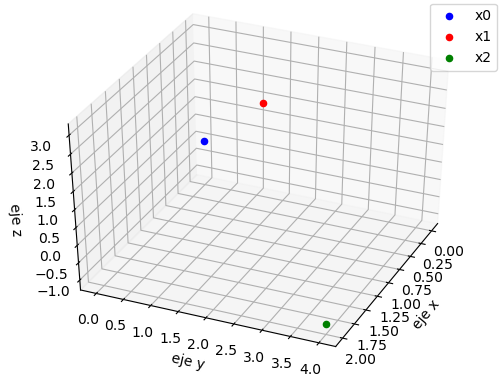
Por ejemplo, si se usan los puntos y se visualizan en un gráfico:
X1 = [ 1 2 3]
X2 = [ 2 4 -1]
errado = |[ 1 2 -4]|
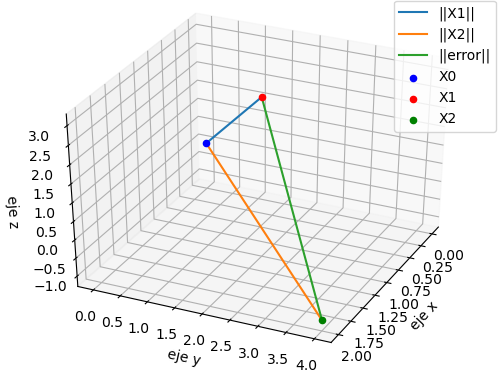
La diferencia entre los vectores |[ 1, 2, -4]| es más simple de observar como un número escalar. Una forma de convertir el punto a un escalar es usar la distancia al origen.
errado = \sqrt{1^2 + 2^2 + (-4)^2} = 4.58El resultado también se interpreta como la distancia entre los puntos X1 y X2
De ampliar el concepto a n dimensiones se conoce como norma de un vector o matriz.
||x|| = \sqrt{x^2+y^2+z^2} ||x|| = \Big[ \sum_{i=0}^{n} x_i ^2 \Big] ^{1/2}Distancia entre dos puntos en el espacio, error y Norma
Observe los siguientes videos, sobre acople de aeronaves.
1. Acoplamiento de aviones para recarca de combustible . www.AiirSource.com. 30/diciembre/2015.
KC-135 Stratotanker in Action – Aircraft Air Refueling
2. Acoplamiento con estación espacial internacional ISS. RT en español . 2/Julio/2010. 
El carguero ruso Progress M-06M pasó de largo la Estación Espacial Internacional fracasado en su intento de acoplarse
- ¿Considera importante que exista acoplamiento para iniciar la carga el combustible? o ¿para abrir la escotilla del transbordador?
Si el error de acoplamiento entre artefactos se calcula como la Norma entre los puntos de «contacto»,
- ¿es necesario calcular la raiz cuadrada de los cuadrados de las diferencias? o,
- ¿Solo toma en cuenta el mínimo o el máximo de las diferencias entre las coordenadas?,
- ¿cuál de las formas tiene menos operaciones, es más rápida de realizar?
considere sus respuestas para el siguiente concepto.
Norma infinito
Se determina como el valor mas grande entre los elementos del vector o matriz.
||x|| = max\Big[ |x_i| \Big]Es más sencilla de calcular que la Norma Ecuclidiana, Norma P=2, mostrada al principio.
Se interpreta como si alguna de las diferencia entre las coordenadas de los puntos de acople entre aeronaves es mayor que lo tolerado, no se debe permitir abrir la válvula de combustible o la escotilla del transbordador. No es prioritario calcular la suma de los cuadrados de las diferencias para saber que no existe acople aún.
Existen otras formas de calcular la Norma, que se presentan en la siguiente página web.
Algoritmo en Python
Principalmente se usa para generar las gráficas 3D, que ayudan a la interpretación del concepto con los puntos de coordenadas:
X0 = np.array([0.0, 0, 0]) X1 = np.array([1.0, 2, 3]) X2 = np.array([2.0, 4,-1])
Las instrucciones gráficas principales son:
- Para puntos, gráficos de dispersión o scatter()
- Para las lineas, gráficos de línea o plot()
El resultado de la parte numérica se obtiene con pocas instrucciones en el bloque de procedimiento
X1 = [1 2 3] X2 = [ 2 4 -1] errado = [-1 -2 4] ||errado|| = 4.58257569495584 Norma euclidiana : 4.58257569495584
las intrucciones en Python son:
# Norma como error # o distancia entre dos puntos # caso 3D import numpy as np # INGRESO X0 = np.array([0.0, 0, 0]) X1 = np.array([1.0, 2, 3]) X2 = np.array([2.0, 4,-1]) # PROCEDIMIENTO errado = X1 - X2 distancia = np.sqrt(np.sum(errado**2)) # funciones numpy Nerrado = np.linalg.norm(errado) # SALIDA print('X1 = ', X1) print('X2 = ', X2) print('errado = ', errado) print('||errado|| = ', distancia) print('Norma euclidiana : ',Nerrado) # Grafica import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D figura = plt.figure() grafica = figura.add_subplot(111,projection = '3d') # puntos en el espacio [x, y , z] = X0 grafica.scatter(x,y,z, c = 'blue', marker='o', label = 'X0') [x, y , z] = X1 grafica.scatter(x,y,z, c = 'red', marker='o', label = 'X1') [x, y , z] = X2 grafica.scatter(x,y,z, c = 'green', marker='o', label = 'X2') # líneas entre puntos linea = np.concatenate(([X0],[X1]),axis = 0) x = linea[:,0] y = linea[:,1] z = linea[:,2] grafica.plot(x,y,z, label = '||X1||') linea = np.concatenate(([X0],[X2]),axis = 0) x = linea[:,0] y = linea[:,1] z = linea[:,2] grafica.plot(x,y,z, label = '||X2||') linea = np.concatenate(([X1],[X2]),axis = 0) x = linea[:,0] y = linea[:,1] z = linea[:,2] grafica.plot(x,y,z, label = '||error||') grafica.set_xlabel('eje x') grafica.set_ylabel('eje y') grafica.set_zlabel('eje z') grafica.legend() grafica.view_init(35, 25) plt.show()