[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..
1. Interpolación por Diferencias finitas avanzadas
Referencia: Rodríguez 6.6.4 p221, Burden 9Ed p129
Se usa en interpolación cuando los puntos en el "eje x" se encuentran igualmente espaciados, la diferencia entre puntos consecutivos xi es una constante denominada h.
h = xi+1 - xi

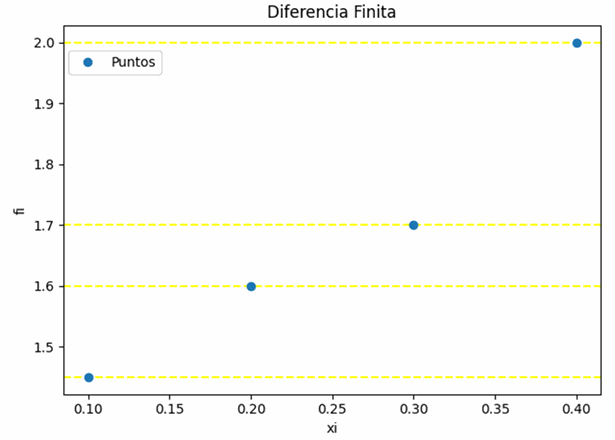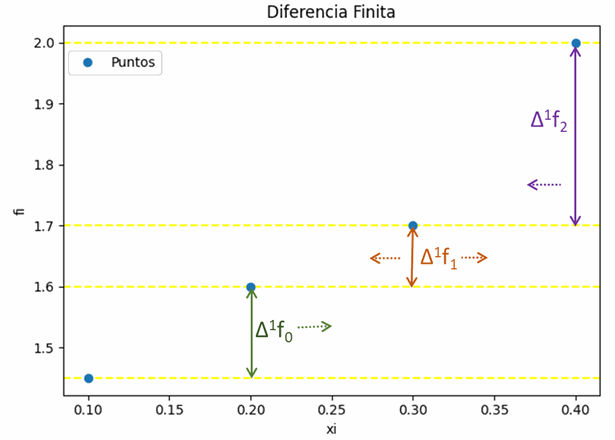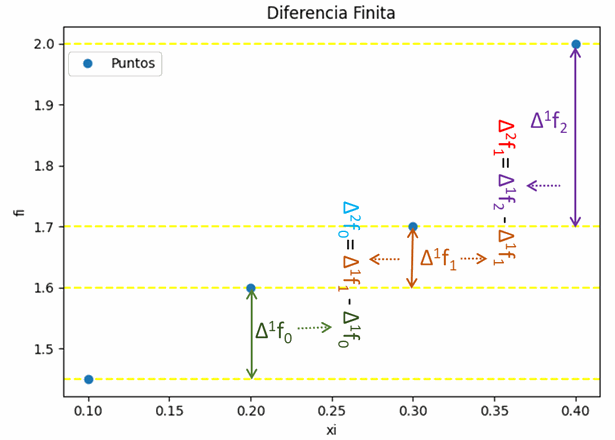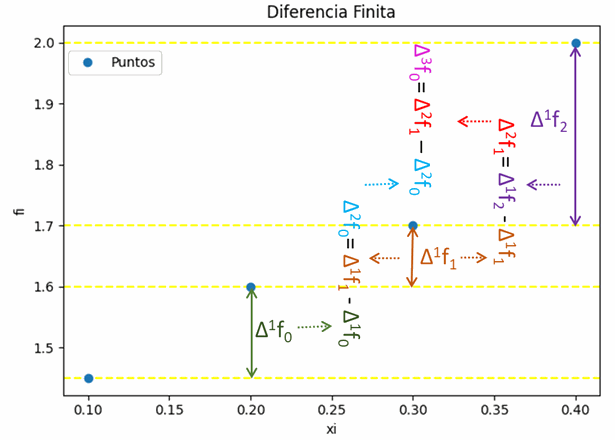
Una relación entre derivadas y diferencias finitas se establece mediante: f^{(n)}(z) = \frac{\Delta ^{n} f_{0}}{h^{n}} para algún z en el intervalo [x0,xn].
\frac{\Delta ^{n} f_{0}}{h^{n}} es una aproximación para la n-ésima derivada f(n)
El polinomio de interpolación se puede construir por medio de diferencias finitas avanzadas con las siguiente fórmula:
p_n (x) = f_0 + \frac{\Delta f_0}{h} (x - x_0) + + \frac{\Delta^2 f_0}{2!h^2} (x - x_0)(x - x_1) + + \frac{\Delta^3 f_0}{3!h^3} (x - x_0)(x - x_1)(x - x_2) + \text{...} + \frac{\Delta^n f_0}{n!h^n} (x - x_0)(x - x_1) \text{...} (x - x_{n-1})Observe que en la medida que se toman más puntos de muestra, el grado del polinomio puede ser mayor.
[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..
2. Ejercicio
Se toman los datos del ejercicio de diferencias finitas , observando que se requiere que el tamaño de paso h sea constante entre los puntos consecutivos xi.
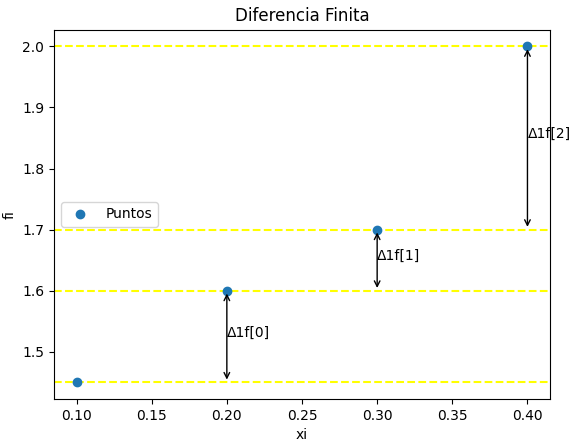
xi = [0.1, 0.2, 0.3, 0.4] fi = [1.45, 1.6, 1.7, 2.0]
| xi | 0.1 | 0.2 | 0.3 | 0.4 |
| fi | 1.45 | 1.6 | 1.7 | 2.0 |
Para éste ejercicio se comprueba que h = 0.1
[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..
3. Desarrollo Analítico
Se inicia el cálculo de la distancia entre puntos xi, comprobando que debe ser constante h, además que los valores xi deben encontrarse ordenados de forma ascendente:
h = xi[1] - xi[0] = 0.2-0.1 = 0.1
h = xi[2] - xi[1] = 0.3-0.2 = 0.1
h = xi[3] - xi[2] = 0.4-0.3 = 0.1
Se usan los resultados previos del ejercicio con diferencias finitas:
Tabla Diferencia Finita: [['i', 'xi', 'fi', 'd1f', 'd2f', 'd3f', 'd4f']] [[ 0. 0.1 1.45 0.15 -0.05 0.25 0. ] [ 1. 0.2 1.6 0.1 0.2 0. 0. ] [ 2. 0.3 1.7 0.3 0. 0. 0. ] [ 3. 0.4 2. 0. 0. 0. 0. ]]
Como los tamaños de paso en xi son constantes, h=0.1, es posible usar el método. Para la construcción del polinomio, se usan los valores de diferencias finitas de la primera fila desde la columna 3 en adelante.
dfinita = tabla[0,3:] = [0.15, -0.05, 0.25, 0.]
Se empieza con el valor del primer punto de la función f(0.1), j=0.
p3(x) = f0 = 1.45
para añadirle el término j=1, más el factor por calcular:
completando el término como:
término = factor(x-x_0) = 1.5(x-0.1) p_3(x) = 1.45 + 1.5(x-0.1)Para el segundo término j=2, se repite el proceso:
factor = \frac{\Delta^2 f_0}{2!h^2} = \frac{-0.05}{2!(0.1)^2} = -2.5 término = factor(x-x_0) = -2.5(x-0.1)(x-0.2) p_3(x)= 1.45 + 1.5(x-0.1) +(-2.5)(x-0.1)(x-0.2)Finalmente, añadiendo el término j=3 cuyo cálculo es semejante a los anteriores, se deja como tarea.
El resultado del método es:
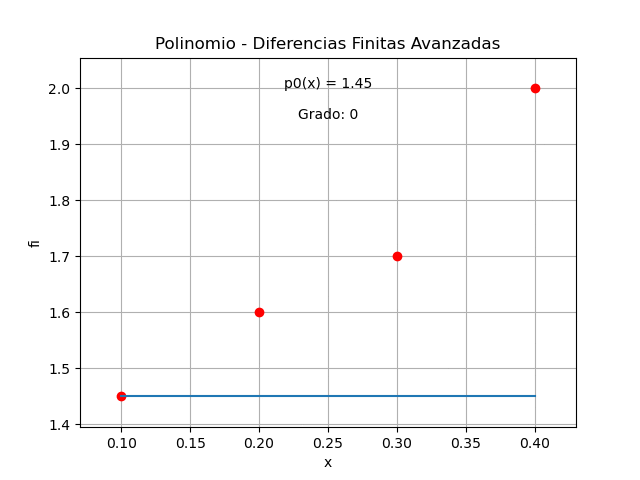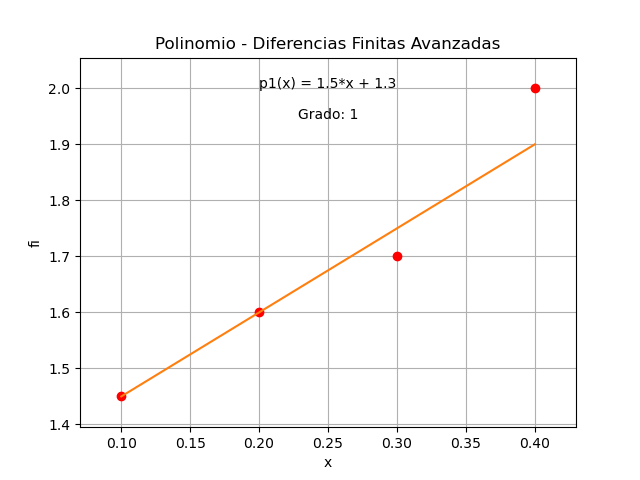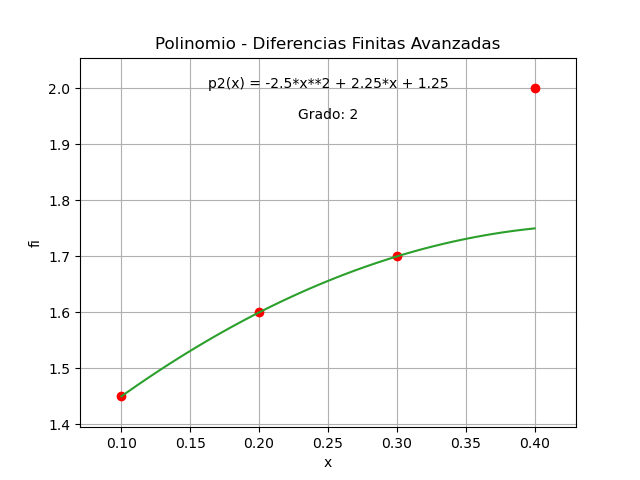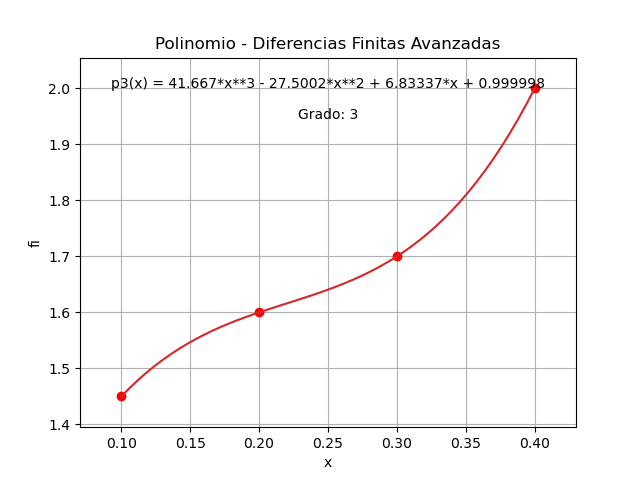
p_3(x)= 1.45 + 1.5(x-0.1) -2.5(x-0.1)(x-0.2) + + 41.667(x - 0.3)(x - 0.2)(x - 0.1)Se puede seguir simplificando la respuesta, por ejemplo usando solo el término de grado con 1.5(x-0.1) se tiene que:
p_3(x) = 1.3 + 1.5x -2.5(x-0.1)(x-0.2)+ + 41.667(x - 0.3)(x - 0.2)(x - 0.1)Seguir simplificando la expresión en papel, se deja como tarea.
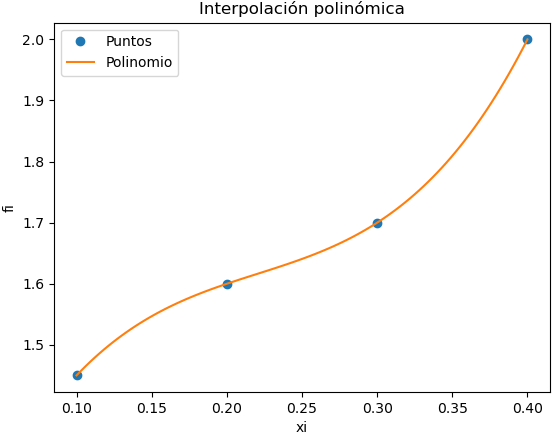
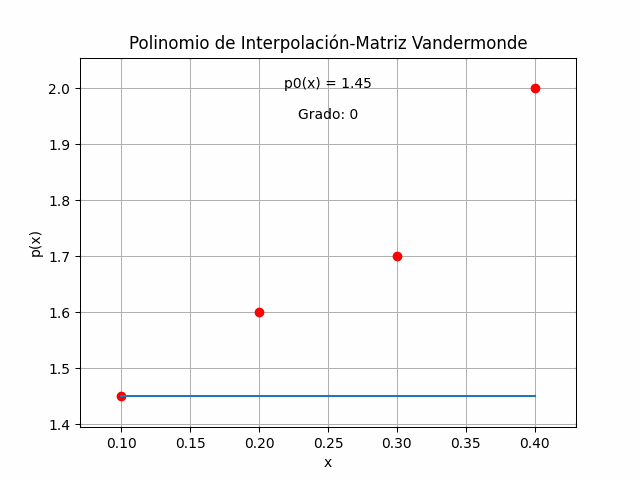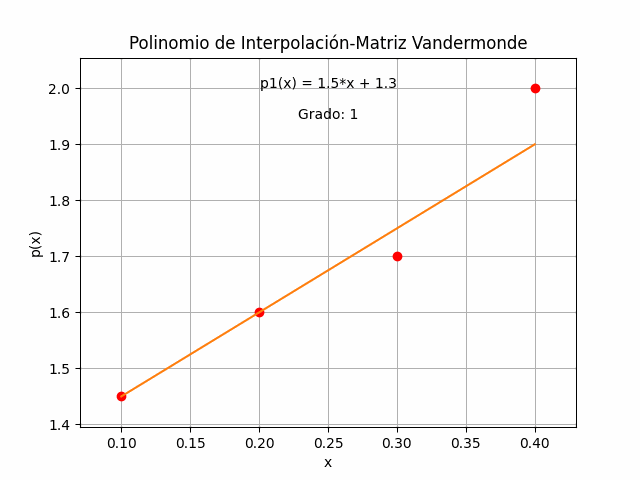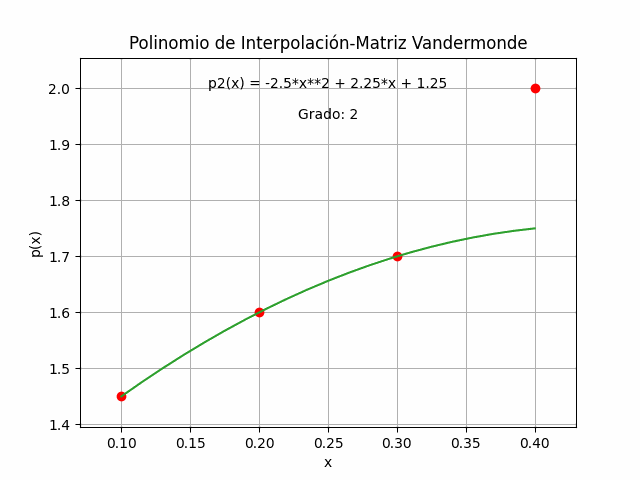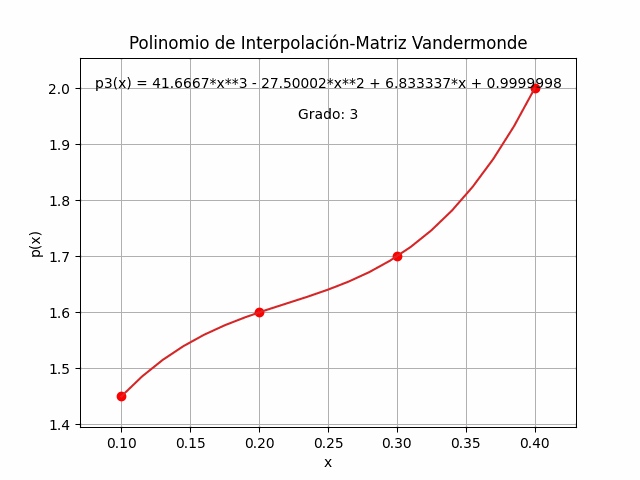
La gráfica del polinomio obtenido comprueba que pasa por cada uno de los puntos dados para el ejercicio.
[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..
4. Algoritmo en Python
El polinomio se construye usando el ejercicio de diferencias finitas.
Para construir la expresión del polinomio añadiendo los términos de la fórmula, se define la variable simbólica x con Sympy.
Para simplificar el polinomio resultante con las expresiones de multiplicación, se utiliza la instrucción sym.expand().
En caso de requerir evaluar la fórmula con un vector de datos se la convierte a la forma lambda para evaluación numérica.
Se añaden las instrucciones para realizar la gráfica en el intervalo [a,b] dado por los valores xi, definiendo el número de muestras = 21 que son suficientes para que la gráfica se observe sin distorsión.
Se añade un bloque para la revisión que los puntos xi sean equidistantes y se encuentren en orden.
# Diferencias finitas Avanzadas - Interpolación # Tarea: Verificar tamaño de vectores import numpy as np import math import sympy as sym # INGRESO xi = [0.1, 0.2, 0.3, 0.4] fi = [1.45, 1.6, 1.7, 2.0] # PROCEDIMIENTO casicero = 1e-15 # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) msj = [] # mensajes de error # xi revisar orden ascendente tramos = np.diff(xi,1) # diferencias en xi donde = -1 # suponer ordenados i = 0 while i<(n-1) and donde<0: if tramos[i]<0: donde = i+1 msj.append(['sin orden en',donde]) i = i+1 # xi tramos desiguales o no equidistantes if (n-1)>=2: # len(tramos)>=2 dtramos = np.diff(tramos,1) # cero o menores a casicero errado = np.max(np.abs(dtramos)) # |error| mayor donde = -1 # suponer equidistantes if errado>=casicero: # no equidistantes donde = np.argmax(np.abs(dtramos))+1 msj.append(['no equidistantes',donde]) # Tabla de Diferencias Finitas tabla_etiq = ['i','xi','fi'] ki = np.arange(0,n,1) # filas tabla = np.concatenate(([ki],[xi],[fi]),axis=0) tabla = np.transpose(tabla) dfinita = np.zeros(shape=(n,n),dtype=float) tabla = np.concatenate((tabla,dfinita), axis=1) n,m = np.shape(tabla) # Calular tabla de Diferencias Finitas diagonal = n-1 # derecha a izquierda j = 3 # inicia en columna 3 while (j < m): # columna tabla_etiq.append('d'+str(j-2)+'f') i = 0 # fila while (i < diagonal): # antes de diagonal tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1] if abs(tabla[i,j])<casicero: # casicero revisa tabla[i,j]=0 i = i + 1 diagonal = diagonal - 1 j = j + 1 dfinita = tabla[0,3:] # diferencias finitas h = xi[1] - xi[0] # suponer tramos equidistantes # polinomio con diferencias Finitas Avanzadas x = sym.Symbol('x') polinomio = fi[0] +0*x # en Sympy for i in range(1,n,1): denominador = math.factorial(i)*(h**i) factor = dfinita[i-1]/denominador termino = 1 for j in range(0,i,1): termino = termino*(x-xi[j]) polinomio = polinomio + termino*factor polisimple = polinomio.expand() # simplifica los (x-xi) px = sym.lambdify(x,polisimple) # evaluación numérica # SALIDA if len(msj)>0: # mensajes de error print('Revisar tramos, d1x:',tramos) for unmsj in msj: print('Tramos',unmsj[0], 'desde i:',unmsj[1]) else: print('Tramo h:',h) print('Tabla Diferencia Finita') print([tabla_etiq]) print(tabla) print('dfinita: ') print(dfinita) print('polinomio: ') print(polinomio) print('polinomio simplificado: ' ) print(polisimple)
teniendo como resultado:
Tramo h: 0.1 Tabla Diferencia Finita [['i', 'xi', 'fi', 'd1f', 'd2f', 'd3f', 'd4f']] [[ 0. 0.1 1.45 0.15 -0.05 0.25 0. ] [ 1. 0.2 1.6 0.1 0.2 0. 0. ] [ 2. 0.3 1.7 0.3 0. 0. 0. ] [ 3. 0.4 2. 0. 0. 0. 0. ]] dfinita: [ 0.15 -0.05 0.25 0. ] polinomio: 1.5*x + 41.6666666666667*(x - 0.3)*(x - 0.2)*(x - 0.1) - 2.50000000000001*(x - 0.2)*(x - 0.1) + 1.3 polinomio simplificado: 41.6666666666667*x**3 - 27.5*x**2 + 6.83333333333335*x + 0.999999999999999
el polinomio de puede evaluar como px(valor) una vez que se convierte a la forma lambda para usar con Numpy:
>>> px(0.1) 1.4500000000000004 >>> px(0.2) 1.6000000000000025 >>> px0.3) 1.7000000000000042 >>>
[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..
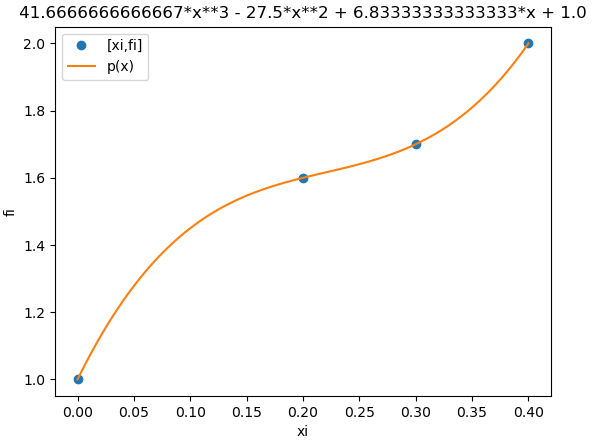
5. Gráfica de polinomio de interpolación
Las instrucciones son semejantes a las presentadas en polinomio de interpolación. Se añade instrucciones para el caso en que los puntos no sean equidistantes en el eje de las x.
Como el bloque de gráfica se usa en otros métodos de la unidad, se incorpora la verificación de lista de errores 'msj' usando el bloque 'try-except'.
# GRAFICA -------------- import matplotlib.pyplot as plt titulo = 'Interpolación: Diferencias Finitas Avanzadas' muestras = 21 # resolución gráfica a = np.min(xi) # intervalo [a,b] b = np.max(xi) xk = np.linspace(a,b,muestras) yk = px(xk) plt.plot(xi,fi,'o', label='[xi,fi]') plt.plot(xk,yk, label='p(x)') try: # existen mensajes de error msj_existe = len(msj) except NameError: msj = [] if len(msj)>0: # tramos con error untipo = msj[0][0] donde = msj[0][1] # indice error plt.plot(xi[donde:donde+2],fi[donde:donde+2], 'ro',label=untipo) plt.plot(xi[donde:donde+2],fi[donde:donde+2], 'r--') plt.xlabel('xi') plt.ylabel('fi') plt.legend() plt.title(titulo) plt.show()
Tarea: se recomienda realizar las gráficas comparativas entre métodos, debe mostrar la diferencia con los métodos que requieren el tamaño de paso equidistante h, y los que no lo requieren. Permite detectar errores de selección de método para interpolación.
[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..
6. Algoritmo como función
Se reordena el algoritmo para usar funciones, la gráfica es la misma que para el algoritmo sin funciones anterior
El bloque de salida es semejante al resultado anterior. Las funciones pueden ser reutilizadas de ser necesarias en el siguiente método de interpolación.
Tabla de Diferencias finitas [['i', 'xi', 'fi', 'd1f', 'd2f', 'd3f', 'd4f']] [[ 0. 0.1 1.45 0.15 -0.05 0.25 0. ] [ 1. 0.2 1.6 0.1 0.2 0. 0. ] [ 2. 0.3 1.7 0.3 0. 0. 0. ] [ 3. 0.4 2. 0. 0. 0. 0. ]] xi_ascendente: True tramos xi Equidistantes: True Tramo h: 0.1 polinomio: 1.30000000000000 + 1.5*x + -2.50000000000001*(x - 0.2)*(x - 0.1) + 41.6666666666667*(x - 0.3)*(x - 0.2)*(x - 0.1) polinomio simplificado: 41.6666666666667*x**3 - 27.5*x**2 + 6.83333333333335*x + 0.999999999999999
Instrucciones en Python
# Diferencias finitas Avanzadas - Interpolación # funciones dif_finitas # Tarea: Verificar tamaño de vectores import numpy as np import math import sympy as sym def revisa_orden(xi,orden='up'): ''' Revisa orden en vector xi. orden='up': orden ascendente orden='down' : orden descendente resultado: True: xi ordenado, False: xi desordenado y dónde. ''' # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) n = len(xi) msj = [] # mensajes de error # xi revisar orden ascendente o descendente tramos = np.diff(xi,1) # diferencias en xi ordenado = True # suponer ordenados k = 1 # 1: ascendente if orden=='down': k = -1 # -1: descendente donde = -1 i = 0 while i<(n-1) and donde<0: if k*tramos[i]<0: ordenado = False donde = i+1 msj.append(['sin orden',donde]) i = i+1 return([ordenado,msj]) def tramos_equidistantes(xi, casicero = 1e-15): ''' Revisa tamaños de paso h en vector xi. True: h son equidistantes, False: h tiene tamaño de paso diferentes y dónde. ''' # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) n = len(xi) msj = [] # mensajes de error # revisa tamaños de paso desiguales o no equidistantes h_iguales = True if (n-1)>=2: # al menos dos tramos dtramos = np.diff(xi,2) # cero o menores a casicero errado = np.max(np.abs(dtramos)) # |error| mayor if errado>=casicero: # no equidistantes h_iguales=False donde = np.argmax(np.abs(dtramos))+1 msj.append(['no equidistantes',donde]) return([h_iguales,msj]) def diferencias_tabla(xi,fi,tipo='finitas', vertabla=False, casicero = 1e-15, precision=4): '''Genera la tabla de diferencias finitas o divididas tipo = 'finitas, tipo = 'divididas' resultado en: tabla, titulo Tarea: verificar tamaño de vectores ''' # revisa tipo de tabla tipolist = ['finitas','divididas'] if not(tipo in tipolist): print('error de tipo, seleccione:',tipolist) return() prefijo = ['d','f'] if tipo=='divididas': prefijo = ['F[',']'] # Matrices como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) # Tabla de Diferencias Finitas/Divididas tabla_etiq = ['i','xi','fi'] ki = np.arange(0,n,1) # filas tabla = np.concatenate(([ki],[xi],[fi]),axis=0) tabla = np.transpose(tabla) dfinita = np.zeros(shape=(n,n),dtype=float) tabla = np.concatenate((tabla,dfinita), axis=1) n,m = np.shape(tabla) # Calular tabla de Diferencias Finitas/Divididas diagonal = n-1 # derecha a izquierda j = 3 # inicia en columna 3 while (j < m): # columna tabla_etiq.append(prefijo[0]+str(j-2)+prefijo[1]) # paso = j-2 # inicia en 1 i = 0 # fila while (i < diagonal): # antes de diagonal tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1] if tipo=='divididas': # denominador = xi[i+paso]-xi[i] denominador = xi[i+j-2]-xi[i] tabla[i,j] = tabla[i,j]/denominador if abs(tabla[i,j])<casicero: # casicero revisa tabla[i,j]=0 i = i + 1 diagonal = diagonal - 1 j = j + 1 if vertabla==True: np.set_printoptions(precision) print('Tabla de Diferencias',tipo) print([tabla_etiq]) print(tabla) return([tabla, tabla_etiq]) # PROGRAMA --------------------- # INGRESO xi = [0.1, 0.2, 0.3, 0.4] fi = [1.45, 1.6, 1.7, 2.0] tipo_tabla = 'finitas' # PROCEDIMIENTO casicero = 1e-12 # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) xi_ascendente,msj = revisa_orden(xi) h_iguales,msj_h = tramos_equidistantes(xi, casicero = casicero) if len(msj_h)>0: msj.extend(msj_h) tabla,titulo = diferencias_tabla(xi,fi,tipo=tipo_tabla, vertabla=True, casicero = casicero) dfinita = tabla[0,3:] # diferencias finitas h = xi[1] - xi[0] # suponer tramos equidistantes # polinomio con diferencias Finitas Avanzadas/ divididas x = sym.Symbol('x') polinomio = fi[0] +0*x # sym.S.Zero en Sympy for i in range(1,n,1): factor = dfinita[i-1] # diferencias divididas if tipo_tabla=='finitas': # diferencias Finitas Avanzadas denominador = math.factorial(i)*(h**i) factor = factor/denominador termino = 1 for j in range(0,i,1): termino = termino*(x-xi[j]) polinomio = polinomio + termino*factor polisimple = polinomio.expand() # simplifica los (x-xi) px = sym.lambdify(x,polisimple) # evaluacion numerica # SALIDA print('xi_ascendente:',xi_ascendente) print('tramos xi Equidistantes:',h_iguales) if len(msj)>0: # mensajes de error print('Revisar tramos, d1x:',np.diff(xi,1)) for unmsj in msj: print('Tramos',unmsj[0], 'desde i:',unmsj[1]) else: print('Tramo h:',h) print('d'+tipo_tabla+': ') print(dfinita) print('polinomio: ') #print(polinomio) terminos = sym.Add.make_args(polinomio) n_term = len(terminos) for i in range(0,n_term,1): if i<(n_term-1): print(terminos[i],'+') else: print(terminos[i]) print() print('polinomio simplificado: ' ) print(polisimple)
La gráfica se genera con el mismo bloque de instrucciones de la sección gráfica.
[ Dif_Finitas avanzadas ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]