[ Regla trapecio ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

---

1. Regla del Trapecio

Referencia: Chapra 21.1 p621  Burden 4.3 p142, Rodríguez 7.1.1 p27

I \cong \frac{h}{2}(f(x_0)+f(x_1))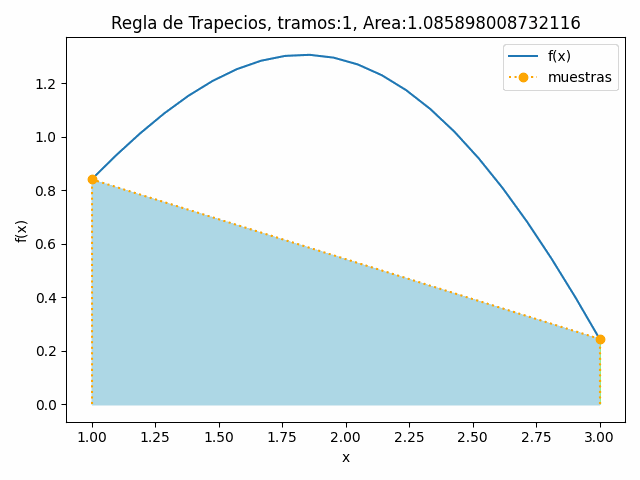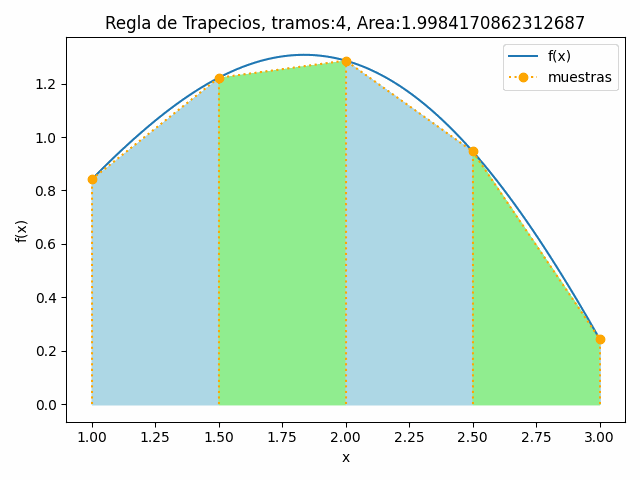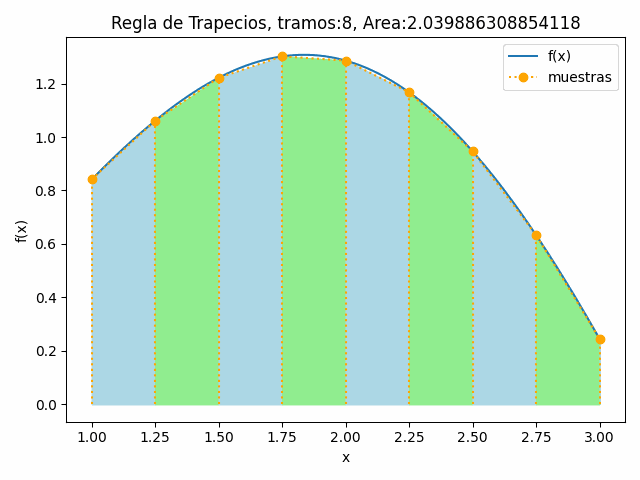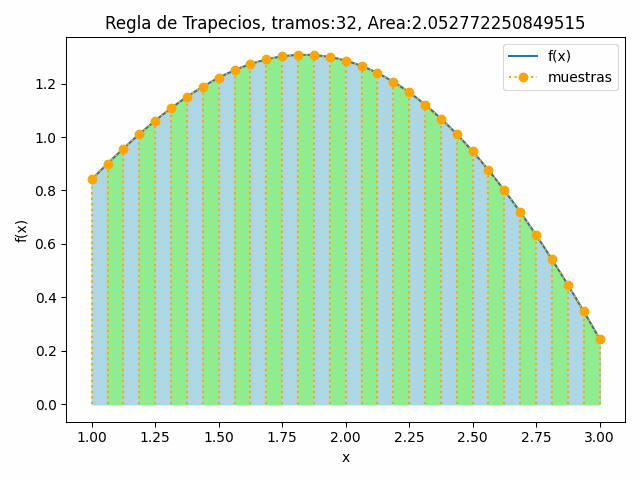

La integración numérica con la regla del trapecio usa un polinomio de primer grado como aproximación de f(x) entre los extremos del intervalo [a,b].

Es la primera de las formulas cerradas de Newton-Cotes.

I = \int_{a}^{b} f(x) dx \cong \int_{a}^{b} f_1 (x) dx

usando el intervalo entre [a,b] el polinomio se aproxima con una línea recta:

f_1 (x) = f(a) + \frac{f(b)-f(a)}{b-a} (x-a)

el área bajo esta línea recta es una aproximación de la integral de f(x) entre los límites a y b

El resultado del integral es la regla del trapecio para el intervalo [a,b]:

I \cong (b-a) \frac{f(a)+f(b)}{2}

que se interpreta como la multiplicación entre la base y altura promedio de un trapecio. También se llega al resultando sumando las áreas de sus componentes: rectángulo y triángulo.

Para disminuir el error, para un intervalo mas grande [a,b] se divide el intervalo en varios tramos de tamaño h. El integral de un tramo se define como:

h = \frac{b-a}{tramos} I \cong \frac{h}{2}(f(x_i)+f(x_i+h)) I \cong \frac{h}{2}(f(x_i)+f(x_{i+1}))

El error de truncamiento se encuentra como el integral del término que le sigue al polinomio de Taylor en la aproximación, es decir el de grado 2, que al integrarlo tiene un orden de h³. (Rodríguez p275)

error_{truncar} = -\frac{h^3}{12}f''(z)

a < z < b

[ Regla trapecio ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

---

2. Ejercicio de Integración con el método del trapecio

Para integrar la función  en el intervalo [1,3] con 4, 16, 32 ,64 y 128 tramos,

f(x)= \sqrt {(x)} \sin(x)

Tramos = 4

El intervalo [1,3] se divide en tramos con tamaño de paso h

h=\frac{b-a}{tramos}=\frac{3-1}{4}= 0.5

para cada tramo, el área de un trapecio es:

A_1 = \frac{0.5}{2} (f(1)+f(1+0.5))= 0.5157 A_2 = \frac{0.5}{2} (f(1.5)+f(1.5+0.5))= 0.6269 A_3 = \frac{0.5}{2} (f(2)+f(2+0.5))= 0.5580 A_4 = \frac{0.5}{2} (f(2.5)+f(2.5+0.5))= 0.2976

y el integral de todo el intervalo es la suma de todos los trapecios.

Integral = A_1+ A_2+ A_3+A_4 = 1.9984

Siguiendo el procedimiento, para cada cantidad de tramos en el intervalo, los resultados serán:

tramos: 4
Integral fx con trapecio: 1.99841708623

tramos:  16
Integral fx con trapecio:  2.05019783717

tramos:  32
Integral fx con trapecio:  2.05277225085

tramos:  64
Integral fx con trapecio:  2.05341563776

tramos: 128
Integral fx con trapecio:  2.05357647096

[ Regla trapecio ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

---

3. Algoritmo para integral f(x) en Python

Algoritmo con fórmula simplificada para varios tramos, con puntos de muestras equidistantes h.

# Regla de los trapecios: f(x) entre [a,b],tramos
import numpy as np

# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)

a = 1  # intervalo de integración
b = 3
tramos = 4 # tramos trapecio

# PROCEDIMIENTO
muestras = tramos + 1
xi = np.linspace(a,b,muestras)
fi = fx(xi)

# Regla del Trapecio
suma = 0 # integral numérico
i = 0
while (i+1)<muestras:
    h = xi[i+1]-xi[i] # incluye tramos desiguales
    trapecio = (h/2)*(fi[i]+fi[i+1])
    suma = suma + trapecio
    i = i+1

# SALIDA
print('tramos: ', tramos)
print('Integral fx con trapecio: ', suma)

[ Regla trapecio ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

---

4. Gráfica de puntos para integrar con trapecio

La gráfica como ayuda didáctica, si la cantidad de tramos sea "poca", muestra los trapecios, si aumenta la cantidad de tramos, no es necesario poner líneas verticales en blanco para separar los trapecios.

La sección de 'fx suave aumentando muestras' se realiza solo si se ha definido la función fx, que permite comparar en la gráfica las diferencias entre fx y los trapecios. Cuando solo se usan muestras, esta sección se omite dentro del algoritmo de la gráfica.

# GRAFICA ---------------------
import matplotlib.pyplot as plt

titulo = 'Regla de Trapecios'
titulo = titulo + ', tramos:'+str(tramos)
titulo = titulo + ', Area:'+str(suma)

try:
    # fx suave aumentando muestras
    muestrasfxSuave = tramos*10 + 1
    xk = np.linspace(a,b,muestrasfxSuave)
    fk = fx(xk)
except NameError:
    # falta variables a,b,muestras y la función fx
    fk = fi # existen solo muestras
    xk = xi

# Trapecios relleno y bordes, cada 1 tramo
for i in range(0,muestras,1):
    x_tramo = xi[i:(i+1)+1]
    f_tramo = fi[i:(i+1)+1]
    
    relleno = 'lightgreen'
    if (i%2)==0: # i múltiplo 2, o par
        relleno ='lightblue'
    plt.fill_between(x_tramo,f_tramo,f_tramo*0,
                     color=relleno)
    # Divisiones entre tramos
    plt.vlines(xi[i],0,fi[i],linestyle='dotted',
               color='orange')

# Graficar f(x), puntos
plt.plot(xk,fk, label ='f(x)')
plt.plot(xi,fi, marker='o',linestyle='dotted',
         color='orange', label ='muestras')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title(titulo)
plt.legend()
plt.tight_layout()

plt.show()

Para rellenar el área bajo la curva con base en eje x, se usa la instrucción plt.fill_between(x_tramo,f_tramo,f_tramo*0,color='green').
La división de los trapecios con una línea naranja (orange) se realiza con la instrucción plt.vlines(xi[i],0,fi[i],linestyle='dotted',color='orange').

[ Regla trapecio ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

---

5. Algoritmo para x[i], f[i] como muestras en Python

Algoritmo usando las muestras y para tramos que pueden tener distancias arbitrarias. En este caso se usa la formula del área del trapecio para cada tramo.

xi = [1. , 1.5, 2. , 2.5, 3. ] 
fi = [0.84147098, 1.22167687, 1.28594075, 0.94626755, 0.24442702]

Usado para ejercicios donde los datos proporcionados son muestras. Se adapta el bloque de ingreso y el procedimiento inicia desde "Regla de Trapecio". La cantidad de tramos será el numero de muestras menos uno tramos = len(xi) - 1 .  La gráfica se realiza con las instrucciones de la sección anterior.

# Regla de los trapecios para muestras xi,fi
import numpy as np

# INGRESO
xi = [1. , 1.5, 2. , 2.5, 3. ]
fi = [0.84147098, 1.22167687, 1.28594075,
      0.94626755, 0.24442702]

# PROCEDIMIENTO
# vectores como arreglo, números reales
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
muestras = len(xi)
tramos = muestras-1

# Regla del Trapecio
suma = 0 # integral numerico
i = 0
while (i+1)<muestras:
    dx = xi[i+1]-xi[i] # incluye tramos desiguales
    trapecio = (dx/2)*(fi[i]+fi[i+1])
    suma = suma + trapecio
    i = i+1

# SALIDA
print('tramos: ',tramos)
print('Integral fx con trapecio: ',suma)

---

[ Regla trapecio ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]