[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]
1. Método de Gauss
Referencia: Chapra 9.2 p254, Burden 6.1 p273, Rodríguez 4.3 p119
El método de Gauss opera sobre la matriz aumentada y pivoteada por filas, añadiendo los procesos:
\begin{cases} a_{0,0} x_0+a_{0,1}x_1+a_{0,2} x_2 = b_{0} \\ a_{1,0} x_0+a_{1,1}x_1+a_{1,2} x_2 = b_{1} \\ a_{2,0} x_0+a_{2,1}x_1+a_{2,2} x_2 = b_{2} \end{cases}1.1 Eliminación hacia adelante
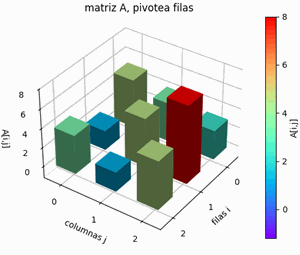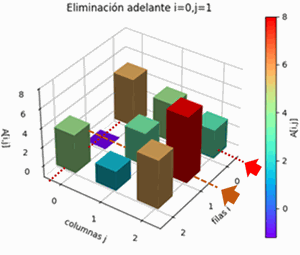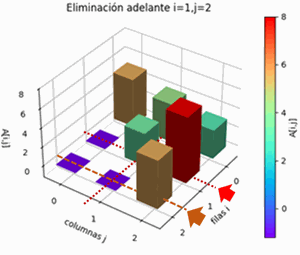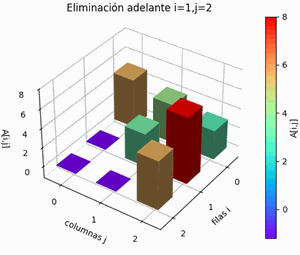Desde la primera fila i ,
sobre las filas inferiores
k = i+1, i+2, ...
a_{k} = a_{k} -a_{i}\frac{a_{ki}}{a_{ii}}1.2 Sustitución hacia atrás
Desde la última fila, para
i = n-1, n-2, ...
x_i = \Bigg( b_i-\sum_{j=i+1}^{n} a_{ij} x_{j} \Bigg) \frac{1}{a_{ii}}y las columnas j luego de la diagonal.
[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]
..
2. Ejercicio
Referencia: Rodríguez 4.0 p105, 1Eva_IT2010_T3_MN Precio artículos
Para el sistema de ecuaciones mostrado, desarrolle usando el método de Gauss.
Se aplica el pivoteo parcial por filas, que tiene como resultado:
[[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]]
[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]
..
3. Eliminación hacia adelante o eliminación Gaussiana
Consiste en simplificar la matriz a una triangular superior, con ceros debajo de la diagonal, usando operaciones entre filas, para obtener:
Elimina hacia adelante [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]]
Los índices de fila y columna en la matriz A[i,j] se usan de forma semejante a la nomenclatura de los textos de Álgebra Lineal. Progresivamente para cada fila, se toma como referencia o pivote el elemento de la diagonal (i=j).
Luego, se realizan operaciones con las filas inferiores para convertir los elementos por debajo de la diagonal en cero.
Las operaciones ya incluyen el vector B debido a que se trabaja sobre la matriz aumentada AB.
AB Matriz aumentada y pivoteada por filas: [[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]]
iteración fila 1, operación fila 1 y 2
Para la fila 1, con posición i=0, se usa el elemento ai,i como pivote.
pivote = AB[i,i] = AB[0,0] = 5
Para las filas que están después de la diagonal se referencian como k. Se obtiene el factor escalar de la operación entre filas de la fórmula.
k = i+1 = 0+1 = 1 factor = AB[1,0]/pivote = 2/5a_{k} = a_{k} -a_{i}\frac{a_{k,i}}{pivote}
y se realiza la operación entre fila k y la fila i para actualizar la fila k,
[ 2. 5. 8. 92.9] -(2/5)*[ 5. 4. 3. 56.3] __________________________ = [ 0. 3.4 6.8 70.38]
con lo que la matriz aumentada AB se actualiza a:
AB = [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 4. 2. 5. 60.7 ]]
iteración fila 1, operación fila 1 y 3
Se continúa con la siguiente fila, quedando la matriz aumentada con la columna debajo de la primera diagonal en cero:
k = k+1 = 2 factor = 4/5
[ 4. 2. 5. 60.7] - (4/5)*[ 5. 4. 3. 56.3] _____________________________ = [ 0. -1.2 2.6 15.66] AB = [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. -1.2 2.6 15.66]]
Como ya se terminaron las operaciones con la primera posición de la diagonal, el siguiente paso es usar la segunda posición, i =1.
iteración fila 2
Para la fila 2, con posición i=1, se toma el elemento de la diagonal ai,i como pivote, la variable adelante indica la referencia de la tercera fila
pivote = A[i,i] = AB[1,1] = 3.4
Para las filas ubicadas adelante de la diagonal se referencian como k. Para aplicar la fórmula por filas, se obtiene el factor .
k = i+1 = 1+1 = 2 factor = AB[2,1]/pivote = -1.2/3.4 = - 0,3529 [ 0. -1.2 2.6 15.66] -(-1.2/3.4)*[ 0. 3.4 6.8 70.38] ________________________________ = [ 0. 0. 5. 40.5 ] AB = [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]]
Con lo que se completa el objetivo de tener ceros debajo de la diagonal.
Observe que no es necesario realizar operaciones para la última fila, por lo que k debe llegar solamente hasta la fila penúltima.
El resultado de la eliminación hacia adelante, a ser usado en el próximo paso es:
\left( \begin{array}{rrr|r} 5 & 4 & 3 & 56.3 \\ 0 & 3.4 & 6.8 & 70.38 \\ 0 & 0 & 5 & 40.5 \end{array} \right)[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]
..
4. Sustitución hacia atrás
La fórmula se interpreta para facilitar el algoritmo.
Desde la última fila, para i = n-1, n-2, ...
Y las columnas j luego de la diagonal
Para una fila i, el vector B[i] representa el valor de la constante en la fila i de la matriz aumentada, A[i,j] se refiere los valores de los coeficientes de la ecuación, de los que se encuentran a la derecha de la diagonal.
Las operaciones se realizan de abajo hacia arriba desde la última fila. Para el ejercicio presentado se tiene que:
ultfila = n-1 = 3-1 = 2
ultcolumna = m-1 = 4-1 = 3
la matriz a procesar es la resultante de eliminación hacia adelante:
\left( \begin{array}{rrr|r} 5 & 4 & 3 & 56.3 \\ 0 & 3.4 & 6.8 & 70.38 \\ 0 & 0 & 5 & 40.5 \end{array} \right)Elimina hacia adelante [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]]
iteración 1, fila 3, i=2
Empieza desde la última fila de la matriz,
[ 0. 0. 5. 40.5 ]0 x_1 + 0 x_2 + 5 x_3 = 40.5
El valor de la constante es B[i] = 40.5 y no existen elementos hacia la derecha de la diagonal. No se usa la ultima columna que es de las constantes:
5 x_3 = 40.5 x_3 = \frac{40.5}{5} = 8.1la respuesta se interpreta en el vector X como:
X= [ x_1 , x_2 , x_3] = [ 0 , 0 , 8.1 ]iteración 2, fila 2, i = 1
De la penúltima fila se obtiene la ecuación para encontrar x2
[ 0. 3.4 6.8 70.38]0x_1 + 3.4 x_2 +6.8 x_3 = 70.38
se observa que B[i] = 70.38 y a la derecha de a diagonal se tiene un solo valor de 6.8.
3.4 x_2 = 70.38 -6.8 x_3 3.4 x_2 = 70.38 -6.8 (8.1)Usa el valor de x3 encontrado en la iteración anterior. Muestra la ecuación para la segunda fila.
x_2 = \frac{70.38 -6.8 (8.1)}{3.4} = 4.5la respuesta se interpreta en el vector X como:
X= [ 0 , 4.5 , 8.1 ]iteración 3 fila 1, i=0
Se sigue el mismo proceso para la siguiente incógnita x1 que se interpreta como
[ 5. 4. 3. 56.3 ]5x_1 + 4 x_2 + 3x_3 = 56.3 5x_1 = 56.3 - ( 4 x_2 + 3x_3) x_1 = \frac{56.3 - ( 4 (4.5) + 3(8.1))}{5} = 2.8
Se encuentra que la solución al sistema de ecuaciones es:
X= [ 2.8, 4.5 , 8.1 ]Método de Gauss solución X: [2.8 4.5 8.1]
Verificar respuesta
Para verificar que el resultado es correcto, se usa el producto punto entre la matriz a y el vector resultado X. La operación A.X = B debe dar el vector B.
>>> A
array([[4., 2., 5.],
[2., 5., 8.],
[5., 4., 3.]])
>>> X
array([2.8, 4.5, 8.1])
>>> np.dot(A,X)
array([60.7, 92.9, 56.3])
[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]
..
5. Algoritmo con Python
El algoritmo para el Método de Gauss, reutiliza las instrucciones para matriz aumentada y pivoteo parcial por filas.
Recordar: Asegurar que los arreglos sean de tipo número Real (float), para que no se considere el vector como entero y realice operaciones entre enteros, generando errores por truncamiento.
El resultado del algoritmo muestra los siguientes resultados:
Pivoteo parcial por filas AB: ---- [[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]] Eliminación hacia adelante: ------ i: 0 k: 1 factor: 0.4 i: 0 k: 2 factor: 0.8 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. -1.2 2.6 15.66]] i: 1 k: 2 factor: -0.3529411764705883 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]] Método de Gauss solución X: [2.8 4.5 8.1]
La parte nueva a desarrollar corresponde al procedimiento de "eliminación hacia adelante" y el procedimiento de "sustitución hacia atrás".
# Método de Gauss # Sistemas de Ecuaciones A.X=B import numpy as np # INGRESO # NOTA: Para AB, se ha usado pivoteo parcial por filas A = [[4,2,5], [2,5,8], [5,4,3]] B = [60.70, 92.90, 56.30] # PROCEDIMIENTO # Matrices como arreglo, numeros reales A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada AB B_columna = np.transpose([B]) AB = np.concatenate((A,B_columna),axis=1) # Pivoteo parcial por filas tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = abs(AB[i:,i]) dondemax = np.argmax(columna) if (dondemax !=0): # NO en diagonal # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal print('Pivoteo parcial por filas AB: ----') print(AB) # Eliminación hacia adelante print('Eliminación hacia adelante: ------') for i in range(0,n-1,1): # una fila pivote = AB[i,i] adelante = i + 1 for k in range(adelante,n,1): # diagonal adelante factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - AB[i,:]*factor print('i:',i,'k:',k, 'factor:',factor) print(AB) # Sustitución hacia atrás ultfila = n-1 ultcolumna = m-1 X = np.zeros(n,dtype=float) for i in range(ultfila,0-1,-1): suma = AB[i,ultcolumna] for j in range(i+1,ultcolumna,1): suma = suma - AB[i,j]*X[j] X[i] = suma/AB[i,i] # SALIDA print('Método de Gauss') print('solución X: ') print(X)
Tarea
Revisar cuando la matriz pivoteada por filas tienen en la diagonal un elemento cero o muy cercano a 0, la matriz sería singular. El valor considerado como casi cero podría ser 1x10-15
A estas alturas, por la cantidad de líneas de instrucción es recomendable reutilizar bloques de algoritmos usando funciones def-return. Por ejemplo: pivoteo por filas, eliminación hacia adelante, sustitución hacia atrás.
[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]
6. Algoritmo como función de Python
Se integra la función pivoteafila(), se crean las funciones para los procedimientos gauss_eliminaAdelante() y gauss_sustituyeAtras(), usando la variable vertabla para observar los resultados parciales.
# Método de Gauss # Sistemas de Ecuaciones A.X=B import numpy as np def gauss_eliminaAdelante(AB,vertabla=False,casicero = 1e-15): ''' Gauss elimina hacia adelante tarea: verificar términos cero ''' tamano = np.shape(AB) n = tamano[0] m = tamano[1] if vertabla==True: print('Elimina hacia adelante:') for i in range(0,n,1): pivote = AB[i,i] adelante = i+1 if vertabla==True: print(' fila i:',i,' pivote:', pivote) for k in range(adelante,n,1): if (np.abs(pivote)>=casicero): factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - factor*AB[i,:] for j in range(0,m,1): # casicero revisa if abs(AB[k,j])<casicero: AB[k,j]=0 if vertabla==True: print(' fila k:',k, ' factor:',factor) else: print(' pivote:', pivote,'en fila:',i, 'genera division para cero') if vertabla==True: print(AB) return(AB) def gauss_sustituyeAtras(AB,vertabla=False,casicero = 1e-15): ''' Gauss sustituye hacia atras ''' n,m = np.shape(AB) # Sustitución hacia atras if vertabla==True: print('Sustitute hacia atras:') X = np.zeros(n,dtype=float) ultfila = n-1 ultcolumna = m-1 for i in range(ultfila,0-1,-1): suma = AB[i,ultcolumna] # B[i] for j in range(i+1,ultcolumna,1): suma = suma - AB[i,j]*X[j] X[i] = suma/AB[i,i] # suma/pivote if vertabla==True: print(' fila i:',i, ' X['+str(i)+']:',X[i]) return(X) def pivoteafila(A,B,vertabla=False): ''' Pivoteo parcial por filas, entrega matriz aumentada AB Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) if vertabla==True: print('Matriz aumentada') print(AB) print('Pivoteo parcial:') # Pivoteo por filas AB tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(' ',pivoteado, 'intercambiar filas: ',i, 'con', dondemax+i) if vertabla==True: if pivoteado==0: print(' Pivoteo por filas NO requerido') else: print('AB:') print(AB) return(AB) # PROGRAMA Búsqueda de solucion -------- # INGRESO A = [[4,2,5], [2,5,8], [5,4,3]] B = [60.70,92.90,56.30] # PROCEDIMIENTO AB = pivoteafila(A,B,vertabla=True) AB = gauss_eliminaAdelante(AB,vertabla=True) X = gauss_sustituyeAtras(AB,vertabla=True) # SALIDA print('Método de Gauss') print('solución X: ') print(X)
El resultado para el ejercicio anterior es:
Matriz aumentada [[ 4. 2. 5. 60.7] [ 2. 5. 8. 92.9] [ 5. 4. 3. 56.3]] Pivoteo parcial: 1 intercambiar filas: 0 con 2 [[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]] Elimina hacia adelante: fila i: 0 pivote: 5.0 fila k: 1 factor: 0.4 fila k: 2 factor: 0.8 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. -1.2 2.6 15.66]] fila i: 1 pivote: 3.4 fila k: 2 factor: -0.3529411764705883 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]] fila i: 2 pivote: 5.0 [[ 5. 4. 3. 56.3 ] [ 0. 3.4 6.8 70.38] [ 0. 0. 5. 40.5 ]] Sustitute hacia atras: fila i: 2 X[2]: 8.100000000000003 fila i: 1 X[1]: 4.499999999999997 fila i: 0 X[0]: 2.8 Método de Gauss solución X: [2.8 4.5 8.1]
[ Gauss ] [ Ejercicio ] [ Eliminación adelante ] [ Sustitución atrás ]
[ Algoritmo ] [ función ]