GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
Solo para fines didácticos, y como complemento para los ejercicios presentados en la unidad para raíces de ecuaciones, se presentan las instrucciones para las animaciones usadas en la presentación de los conceptos y ejercicios. Los algoritmos para animación NO son necesarios para realizar los ejercicios, que requieren una parte analítica con al menos tres iteraciones en papel y lápiz. Se lo adjunta como una herramienta didáctica de asistencia para las clases.
La gráfica (graf_ani) se crea en una ventana (fig_ani), inicializando con la linea a partir f(x) y configurando los parámetros base para el gráfico.
Se usan procedimientos para crear unatrama() para marca de iteración y en cada cambio se limpia la trama manteniendo la base con limpiatrama().
En caso de requerir un archivo .gif animado se proporciona un nombre de archivo. Para crear el archivo se requiere de la librería 'pillow', a ser instalado.
otros ejemplos de animación en el curso de Fundamentos de Programación:
Movimiento circular – Una partícula, animación con matplotlib-Python
GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
..
Método de la Bisección con gráfico animado en Python
# Algoritmo de Bisecci n, Tabla # Los valores de [a,b] son aceptables # y seleccionados desde la gr fica de la funci n # error = tolera import numpy as np def biseccion_tabla(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=6): '''Algoritmo de Bisecci n Los valores de [a,b] son seleccionados desde la gr fica de la funci n error = tolera ''' fa = fx(a) fb = fx(b) tramo = np.abs(b-a) itera = 0 cambia = np.sign(fa)*np.sign(fb) tabla=[] if cambia<0: # existe cambio de signo f(a) vs f(b) if vertabla==True: print('m todo de Bisecci n') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') np.set_printoptions(precision) while (tramo>=tolera and itera<=iteramax): c = (a+b)/2 fc = fx(c) cambia = np.sign(fa)*np.sign(fc) unafila = [a,c,b,fa,fc,fb] if vertabla==True: print(itera,[a,c,b],np.array([fa,fc,fb])) if (cambia<0): b = c fb = fc else: a = c fa = fc tramo = np.abs(b-a) unafila.append(tramo) tabla.append(unafila) if vertabla==True: print(' ',tramo) itera = itera + 1 respuesta = c # Valida respuesta if (itera>=iteramax): respuesta = np.nan else: print(' No existe cambio de signo entre f(a) y f(b)') print(' f(a) =',fa,', f(b) =',fb) respuesta=np.nan tabla = np.array(tabla,dtype=float) return(respuesta,tabla) # PROGRAMA ####################### # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO [raiz,tabla] = biseccion_tabla(fx,a,b,tolera,vertabla=True) # SALIDA print('ra z en: ', raiz) # GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) xc = tabla[:,1] yc = tabla[:,4] plt.plot(xi,fi, label='f(x)') plt.plot([a,b],[fx(a),fx(b)],'o', color='red',label='[[a,b],[f(a),f(b)]]') plt.scatter(xc,yc,color='orange', label='[c,f(c)]') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.title('Bisecci n') plt.grid() plt.legend() #plt.show() # GRAFICA CON ANIMACION ------------ import matplotlib.animation as animation xa = tabla[:,0] ya = tabla[:,3] xb = tabla[:,2] yb = tabla[:,5] xc = tabla[:,1] yc = tabla[:,4] # Inicializa parametros de trama/foto narchivo = 'Biseccion' # nombre archivo retardo = 700 # milisegundos entre tramas tramas = len(xa) # GRAFICA animada en fig_ani fig_ani, graf_ani = plt.subplots() ymax = np.max(fi) ymin = np.min(fi) deltax = np.abs(b-a) deltay = np.abs(ymax-ymin) graf_ani.set_xlim([a-0.05*deltax,b+0.05*deltax]) graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.05*deltay]) linea0 = graf_ani.axhline(0, color='k') # Lineas y puntos base lineafx,= graf_ani.plot(xi,fi, label='f(x)') puntoa, = graf_ani.plot(xa[0], ya[0],'o', color='red', label='a') puntob, = graf_ani.plot(xb[0], yb[0],'o', color='green', label='b') puntoc, = graf_ani.plot(xc[0], yc[0],'o', color='orange', label='c') lineaa, = graf_ani.plot([xa[0],xa[0]], [0,ya[0]],color='red', linestyle='dashed') lineab, = graf_ani.plot([xb[0],xb[0]], [0,yb[0]],color='green', linestyle='dashed') lineac, = graf_ani.plot([xc[0],xc[0]], [0,yc[0]], color='orange', linestyle='dashed') linea_ab, = graf_ani.plot([xa[0],xb[0]], [0,0], color='yellow', linestyle='dotted') # Configura gr fica graf_ani.set_title('Bisecci n') graf_ani.set_xlabel('x') graf_ani.set_ylabel('f(x)') graf_ani.legend() graf_ani.grid() # Cada nueva trama def unatrama(i,xa,ya,xb,yb,xc,yc): # actualiza cada punto puntoa.set_xdata([xa[i]]) puntoa.set_ydata([ya[i]]) puntob.set_xdata([xb[i]]) puntob.set_ydata([yb[i]]) puntoc.set_xdata([xc[i]]) puntoc.set_ydata([yc[i]]) # actualiza cada linea lineaa.set_ydata([ya[i], 0]) lineaa.set_xdata([xa[i], xa[i]]) lineab.set_ydata([yb[i], 0]) lineab.set_xdata([xb[i], xb[i]]) lineac.set_ydata([yc[i], 0]) lineac.set_xdata([xc[i], xc[i]]) linea_ab.set_ydata([0, 0]) linea_ab.set_xdata([xa[i], xb[i]]) return (puntoa, puntob, puntoc, lineaa, lineab, lineac,linea_ab) # Limpia trama anterior def limpiatrama(): puntoa.set_ydata(np.ma.array(xa, mask=True)) puntob.set_ydata(np.ma.array(xb, mask=True)) puntoc.set_ydata(np.ma.array(xc, mask=True)) lineaa.set_ydata(np.ma.array([0,0], mask=True)) lineab.set_ydata(np.ma.array([0,0], mask=True)) lineac.set_ydata(np.ma.array([0,0], mask=True)) linea_ab.set_ydata(np.ma.array([0,0], mask=True)) return (puntoa, puntob, puntoc, lineaa, lineab, lineac,linea_ab) # contador de tramas i = np.arange(0,tramas,1) ani = animation.FuncAnimation(fig_ani,unatrama, i , fargs=(xa, ya, xb, yb, xc, yc), init_func=limpiatrama, interval=retardo, blit=True) # Graba Archivo GIFAnimado y video ani.save(narchivo+'_animado.gif', writer='pillow') #ani.save(narchivo+'_animado.mp4') plt.show()
GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
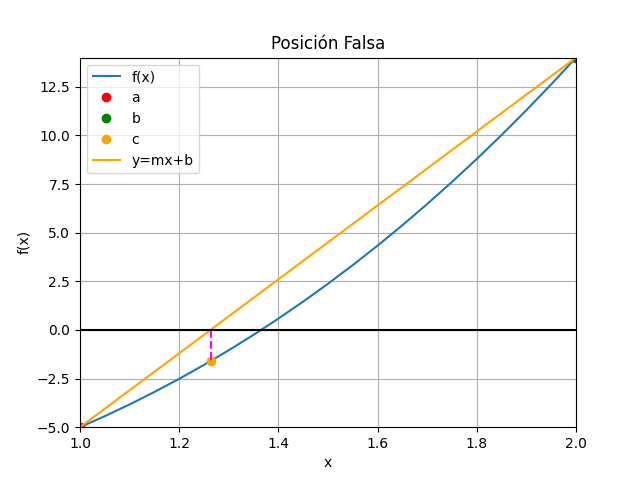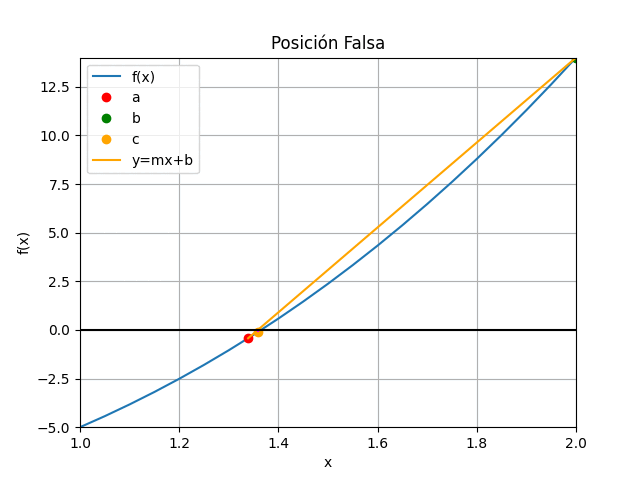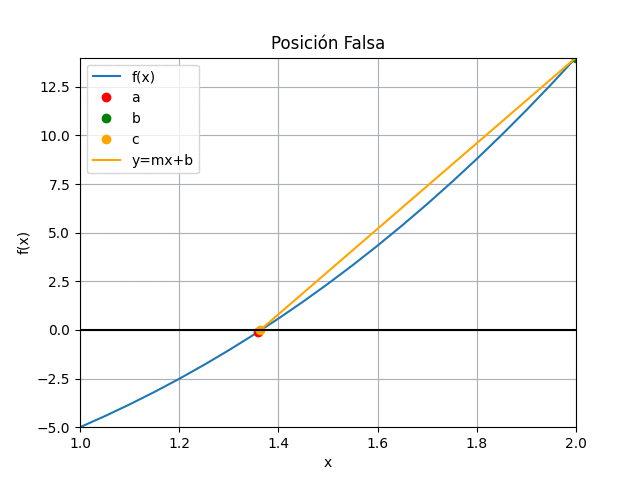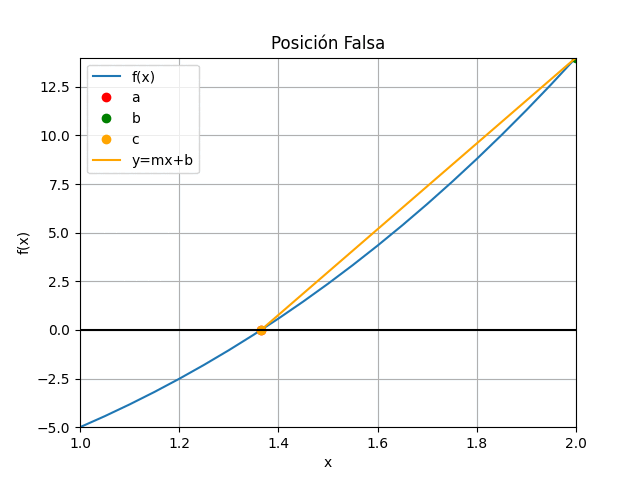
Método de la Posición Falsa con gráfico animado en Python
# Algoritmo de falsa posicion para raices # Los valores de [a,b] son seleccionados # desde la gráfica de la función # error = tolera import numpy as np def posicionfalsa_tabla(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=6): '''fx en forma numérica lambda Los valores de [a,b] son seleccionados desde la gráfica de la función error = tolera ''' fa = fx(a) fb = fx(b) tramo = np.abs(b-a) itera = 0 cambia = np.sign(fa)*np.sign(fb) tabla = [] if cambia<0: # existe cambio de signo f(a) vs f(b) if vertabla==True: print('método de la Posición Falsa ') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') np.set_printoptions(precision) while (tramo >= tolera and itera<=iteramax): c = b - fb*(a-b)/(fa-fb) fc = fx(c) cambia = np.sign(fa)*np.sign(fc) unafila = [a,c,b,fa, fc, fb] if vertabla==True: print(itera,np.array([a,c,b]), np.array([fa,fc,fb])) if (cambia > 0): tramo = np.abs(c-a) a = c fa = fc else: tramo = np.abs(b-c) b = c fb = fc unafila.append(tramo) tabla.append(unafila) if vertabla==True: print(' ',tramo) itera = itera + 1 respuesta = c # Valida respuesta if (itera>=iteramax): respuesta = np.nan else: print(' No existe cambio de signo entre f(a) y f(b)') print(' f(a) =',fa,', f(b) =',fb) respuesta=np.nan tabla = np.array(tabla,dtype=float) return(respuesta,tabla) # PROGRAMA ---------------------- # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 2 tolera = 0.001 # PROCEDIMIENTO [raiz,tabla] = posicionfalsa_tabla(fx,a,b,tolera, vertabla=True) # SALIDA print('raíz en: ', raiz) # GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) xc = tabla[:,1] yc = tabla[:,4] plt.plot(xi,fi, label='f(x)') plt.plot([a,b],[fx(a),fx(b)],'o', color='red',label='[[a,b],[f(a),f(b)]]') plt.scatter(xc,yc,color='orange', label='[c,f(c)]') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.title('Posición Falsa') plt.grid() plt.legend() #plt.show() # GRAFICA CON ANIMACION ------------ #import matplotlib.pyplot as plt import matplotlib.animation as animation xa = tabla[:,0] ya = tabla[:,3] xc = tabla[:,1] yc = tabla[:,4] xb = tabla[:,2] yb = tabla[:,5] # Inicializa parametros de trama/foto narchivo = 'PosicionFalsa' # nombre archivo retardo = 700 # milisegundos entre tramas tramas = len(xa) # GRAFICA animada en fig_ani fig_ani, graf_ani = plt.subplots() graf_ani.set_xlim([a,b]) graf_ani.set_ylim([np.min(fi),np.max(fi)]) # Lineas y puntos base lineafx, = graf_ani.plot(xi,fi,label ='f(x)') puntoa, = graf_ani.plot(xa[0], ya[0],'o', color='red', label='a') puntob, = graf_ani.plot(xb[0], yb[0],'o', color='green', label='b') puntoc, = graf_ani.plot(xc[0], yc[0],'o', color='orange', label='c') lineaab, = graf_ani.plot([xa[0],xb[0]],[ya[0],yb[0]], color ='orange', label='y=mx+b') lineac0, = graf_ani.plot([xc[0],xc[0]],[0,yc[0]], color='magenta', linestyle='dashed') # Configura gráfica linea0 = graf_ani.axhline(0, color='k') graf_ani.set_title('Posición Falsa') graf_ani.set_xlabel('x') graf_ani.set_ylabel('f(x)') graf_ani.legend() graf_ani.grid() # Cada nueva trama def unatrama(i,xa,ya,xc,yc,xb,yb): # actualiza cada punto, [] porque es solo un valor puntoa.set_xdata([xa[i]]) puntoa.set_ydata([ya[i]]) puntob.set_xdata([xb[i]]) puntob.set_ydata([yb[i]]) puntoc.set_xdata([xc[i]]) puntoc.set_ydata([yc[i]]) # actualiza cada linea lineaab.set_ydata([ya[i], yb[i]]) lineaab.set_xdata([xa[i], xb[i]]) lineac0.set_ydata([0, yc[i]]) lineac0.set_xdata([xc[i], xc[i]]) return (puntoa, puntob, puntoc, lineaab,lineac0,) # Cada nueva trama def limpiatrama(): puntoa.set_ydata(np.ma.array(xa, mask=True)) puntob.set_ydata(np.ma.array(xb, mask=True)) puntoc.set_ydata(np.ma.array(xc, mask=True)) lineaab.set_ydata(np.ma.array([0,0], mask=True)) lineac0.set_ydata(np.ma.array([0,0], mask=True)) return (puntoa, puntob, puntoc, lineaab,lineac0,) # contador de tramas i = np.arange(0, tramas,1) ani = animation.FuncAnimation(fig_ani,unatrama, i , fargs=(xa, ya, xc, yc, xb,yb), init_func=limpiatrama, interval=retardo, blit=True) # Graba Archivo GIFAnimado y video ani.save(narchivo+'_animado.gif', writer='pillow') #ani.save(narchivo+'.mp4') plt.show()
GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
..
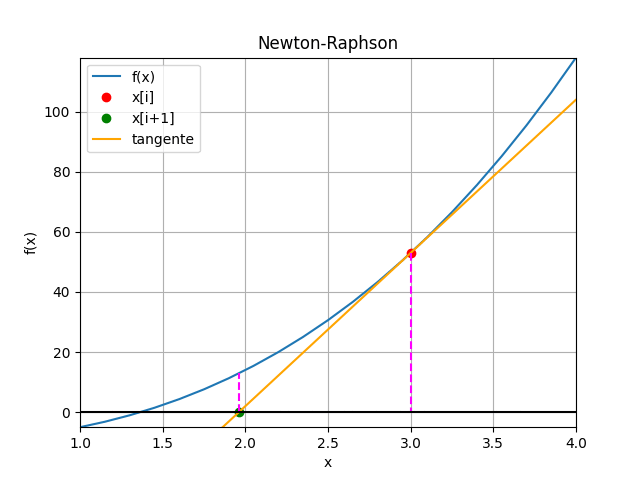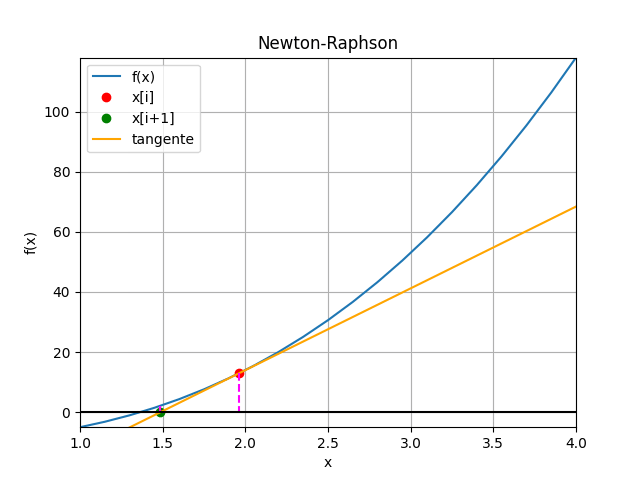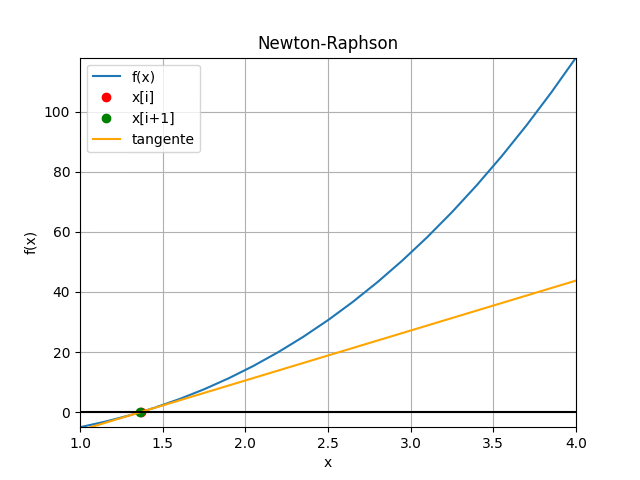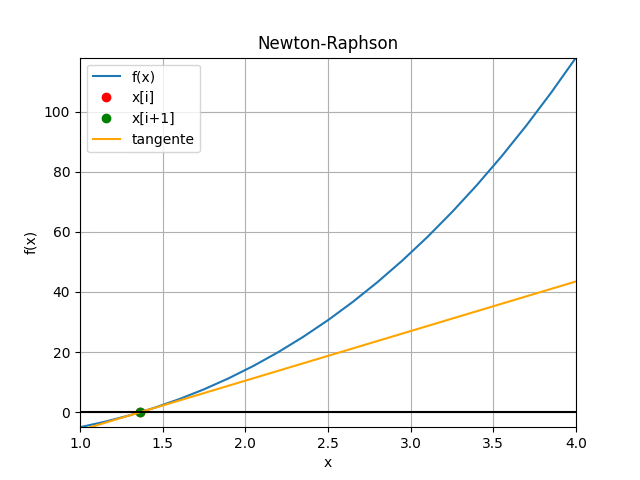
Método de Newton-Raphson con gráfico animado en Python
# Método de Newton-Raphson # Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61) import numpy as np def newton_raphson_tabla(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4): ''' fx y dfx en forma numérica lambda xi es el punto inicial de búsqueda ''' itera=0 tramo = abs(2*tolera) tabla = [] if vertabla==True: print('método de Newton-Raphson') print('i', ['xi','fi','dfi', 'xnuevo', 'tramo']) np.set_printoptions(precision) while (tramo>=tolera): fi = fx(xi) dfi = dfx(xi) xnuevo = xi - fi/dfi tramo = abs(xnuevo-xi) if vertabla==True: print(itera,np.array([xi,fi,dfi,xnuevo,tramo])) tabla.append([xi,fi,dfi,xnuevo,tramo]) xi = xnuevo itera = itera + 1 if itera>=iteramax: xi = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') tabla = np.array(tabla,dtype=float) return(xi,tabla) # PROGRAMA ---------------------- # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 dfx = lambda x: 3*(x**2) + 8*x a = 1 b = 4 x0 = 3 tolera = 0.001 # PROCEDIMIENTO [raiz,tabla] = newton_raphson_tabla(fx, dfx, x0, tolera, vertabla=True) # SALIDA print('raiz en :', raiz) # GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) xc = tabla[:,3] yc = fx(xc) plt.plot(xi,fi, label='f(x)') plt.plot(x0,fx(x0),'o', color='red',label='[x0,f(x0)]') plt.scatter(xc,yc,color='orange', label='[c,f(c)]') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.grid() plt.legend() #plt.show() # GRAFICA CON ANIMACION ------------ #import matplotlib.pyplot as plt import matplotlib.animation as animation xa = tabla[:,0] ya = tabla[:,1] xb = tabla[:,3] dfi = tabla[:,2] # Aproximacion con tangente b0 = ya[0] - dfi[0]*x0 tangentei = dfi[0]*xi + b0 ci = -b0/dfi[0] # Inicializa parametros de trama/foto narchivo = 'NewtonRaphson' # nombre archivo retardo = 700 # milisegundos entre tramas tramas = len(xa) # GRAFICA animada en fig_ani fig_ani, graf_ani = plt.subplots() graf_ani.set_xlim([a,b]) graf_ani.set_ylim([np.min(fi),np.max(fi)]) # Lineas y puntos base lineafx, = graf_ani.plot(xi,fi,label ='f(x)') puntoa, = graf_ani.plot(xa[0], ya[0],'o', color='red', label='x[i]') puntob, = graf_ani.plot(xb[0], 0,'o', color='green', label='x[i+1]') lineatanx, = graf_ani.plot(xi,tangentei, color='orange',label='tangente') lineaa, = graf_ani.plot([xa[0],xa[0]], [ya[0],0], color='magenta', linestyle='dashed') lineab, = graf_ani.plot([xb[0],xb[0]], [0,fx(xb[0])], color='magenta', linestyle='dashed') # Configura gráfica linea0 = graf_ani.axhline(0, color='k') graf_ani.set_title('Newton-Raphson') graf_ani.set_xlabel('x') graf_ani.set_ylabel('f(x)') graf_ani.legend() graf_ani.grid() # Cada nueva trama def unatrama(i,xa,ya,xb,dfi): # actualiza cada punto, [] porque es solo un valor puntoa.set_xdata([xa[i]]) puntoa.set_ydata([ya[i]]) puntob.set_xdata([xb[i]]) puntob.set_ydata([0]) # actualiza cada linea lineaa.set_ydata([ya[i], 0]) lineaa.set_xdata([xa[i], xa[i]]) lineab.set_ydata([0, fx(xb[i])]) lineab.set_xdata([xb[i], xb[i]]) # Aproximacion con tangente b0 = ya[i] - dfi[i]*xa[i] tangentei = dfi[i]*xi+b0 lineatanx.set_ydata(tangentei) return (puntoa, puntob, lineaa, lineab,lineatanx,) # Limpia trama anterior def limpiatrama(): puntoa.set_ydata(np.ma.array(xa, mask=True)) puntob.set_ydata(np.ma.array(xb, mask=True)) lineaa.set_ydata(np.ma.array([0,0], mask=True)) lineab.set_ydata(np.ma.array([0,0], mask=True)) lineatanx.set_ydata(np.ma.array(xi, mask=True)) return (puntoa, puntob, lineaa, lineab,lineatanx,) # contador de tramas i = np.arange(0,tramas,1) ani = animation.FuncAnimation(fig_ani,unatrama, i , fargs=(xa, ya, xb, dfi), init_func=limpiatrama, interval=retardo, blit=True) # Graba Archivo GIFAnimado y video ani.save(narchivo+'_animado.gif', writer='pillow') #ani.save(narchivo+'.mp4') plt.show()
GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
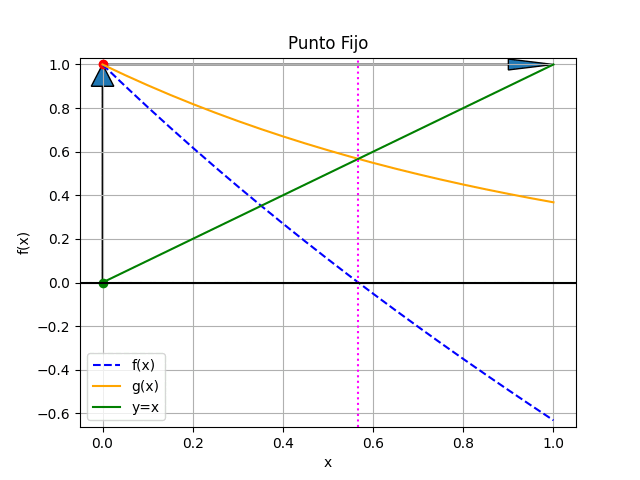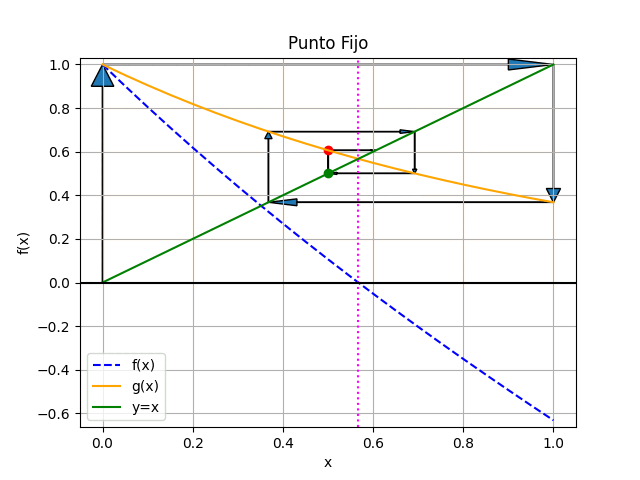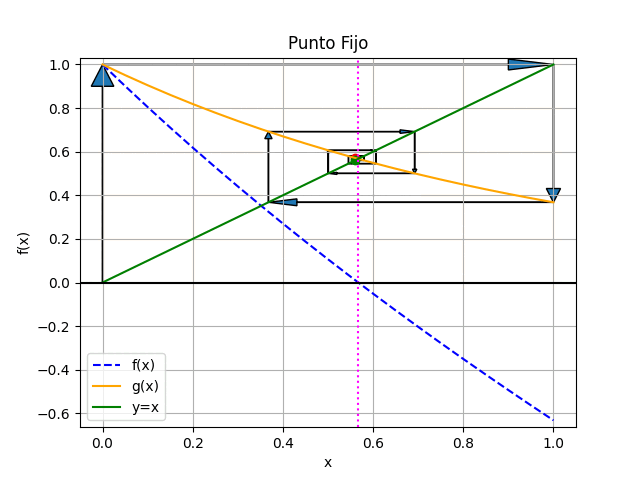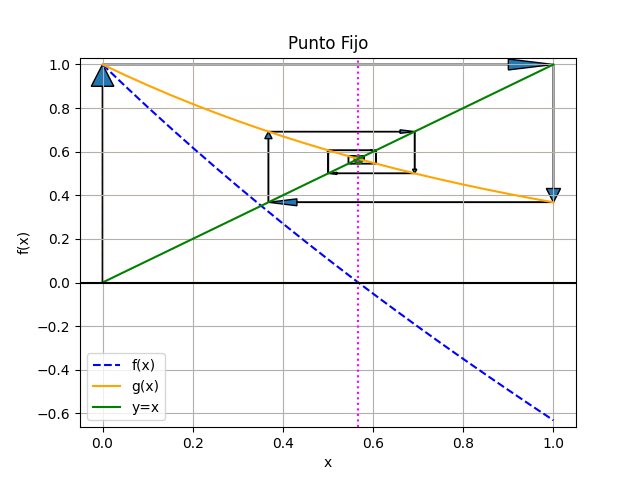
Método del Punto Fijo con gráfico animado en Python
# Algoritmo de punto fijo, Tabla # Los valores de [a,b] son seleccionados # desde la gráfica de la función # error = tolera import numpy as np def puntofijo_tabla(gx,a,tolera, iteramax=20, vertabla=True, precision=6): '''g(x) se obtiene al despejar una x de f(x) máximo de iteraciones predeterminado: iteramax si no converge hasta iteramax iteraciones la respuesta es NaN (Not a Number) ''' itera = 0 b = gx(a) tramo = abs(b-a) tabla = [[a,b,tramo]] if vertabla==True: print('método del Punto Fijo') print('i', ['xi','gi','tramo']) np.set_printoptions(precision) print(itera,np.array([a,b,tramo])) while(tramo>=tolera and itera<=iteramax): a = b b = gx(a) tramo = abs(b-a) itera = itera + 1 if vertabla==True: print(itera,np.array([a,b,tramo])) tabla.append([a,b,tramo]) respuesta = b # Valida respuesta if itera>=iteramax: respuesta = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') tabla = np.array(tabla,dtype=float) return(respuesta,tabla) # PROGRAMA ---------------------- # INGRESO fx = lambda x: np.exp(-x) - x gx = lambda x: np.exp(-x) a = 0 b = 1 tolera = 0.001 # PROCEDIMIENTO [raiz,tabla] = puntofijo_tabla(gx,a,tolera, vertabla=True) # SALIDA print('raiz en :', raiz) # GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) gi = gx(xi) yi = xi plt.plot(xi,fi, label='f(x)', linestyle='dashed') plt.plot(xi,gi, label='g(x)') plt.plot(xi,yi, label='y=x') plt.axvline(raiz, color='magenta', linestyle='dotted') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.title('Punto Fijo') plt.grid() plt.legend() #plt.show() # GRAFICA CON ANIMACION ------------ #import matplotlib.pyplot as plt import matplotlib.animation as animation xc = tabla[:,0] yc = tabla[:,1] # Inicializa parametros de trama/foto narchivo = 'PuntoFijo' # nombre archivo retardo = 700 # milisegundos entre tramas tramas = len(xc) # GRAFICA animada en fig_ani fig_ani, graf_ani = plt.subplots() dx = np.abs(b-a) dy = np.abs(gx(b)-gx(a)) graf_ani.set_xlim([a-0.05*dx,b+0.05*dx]) graf_ani.set_ylim([np.min(fi)-0.05*dy,np.max(fi)+0.05*dy]) # Lineas y puntos base puntoa, = graf_ani.plot(xc[0], yc[0], 'ro') puntob, = graf_ani.plot(xc[0], xc[0], 'go') # y=x lineafx, = graf_ani.plot(xi,fi, color='blue', linestyle='dashed', label='f(x)') lineagx, = graf_ani.plot(xi,gi, color='orange', label='g(x)') lineayx, = graf_ani.plot(xi,yi, color='green', label='y=x') linearaiz = graf_ani.axvline(raiz, color='magenta',linestyle='dotted') # Configura gráfica linea0 = graf_ani.axhline(0, color='k') graf_ani.set_title('Punto Fijo') graf_ani.set_xlabel('x') graf_ani.set_ylabel('f(x)') graf_ani.legend() graf_ani.grid() # Cada nueva trama def unatrama(i,xc,yc): # actualiza cada punto, [] porque es solo un valor puntoa.set_xdata([xc[i]]) puntoa.set_ydata([yc[i]]) puntob.set_xdata([xc[i]]) # y=x puntob.set_ydata([xc[i]]) # actualiza cada flecha dx = xc[i+1]-xc[i] dy = yc[i]-xc[i] flecha01 = graf_ani.arrow(xc[i],xc[i], 0,dy, length_includes_head = True, head_width = 0.05*abs(dy), head_length = 0.1*abs(dy)) flecha02 = graf_ani.arrow(xc[i],yc[i], dx,0, length_includes_head = True, head_width = 0.05*abs(dx), head_length = 0.1*abs(dx)) return (puntoa, puntob, flecha01, flecha02) # Limpia trama anterior def limpiatrama(): puntoa.set_ydata(np.ma.array([xc[0]], mask=True)) puntob.set_ydata(np.ma.array([xc[0]], mask=True)) return (puntoa, puntob) # contador de tramas i = np.arange(0, tramas-1,1) ani = animation.FuncAnimation(fig_ani,unatrama, i , fargs=(xc, yc), init_func=limpiatrama, interval=retardo, blit=True) # Graba Archivo GIFAnimado y video ani.save(narchivo+'_animado.gif', writer='pillow') #ani.save(narchivo+'.mp4') plt.show()
GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]
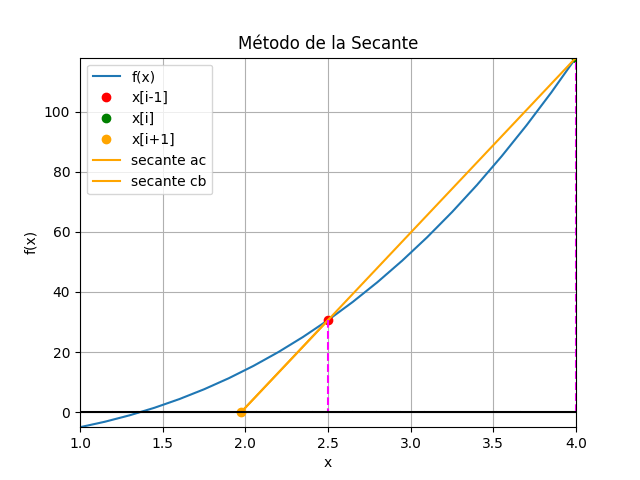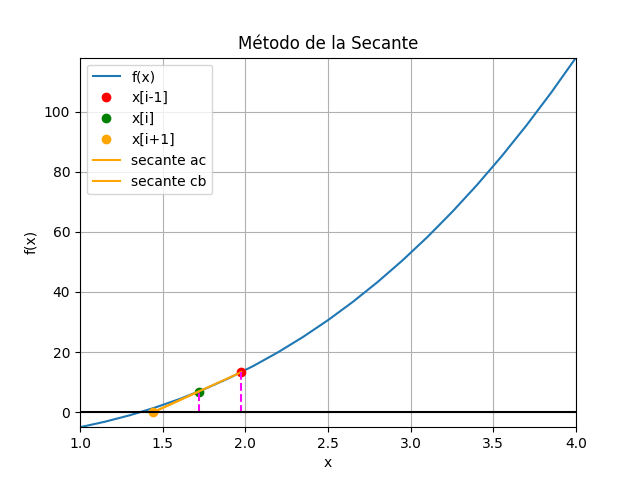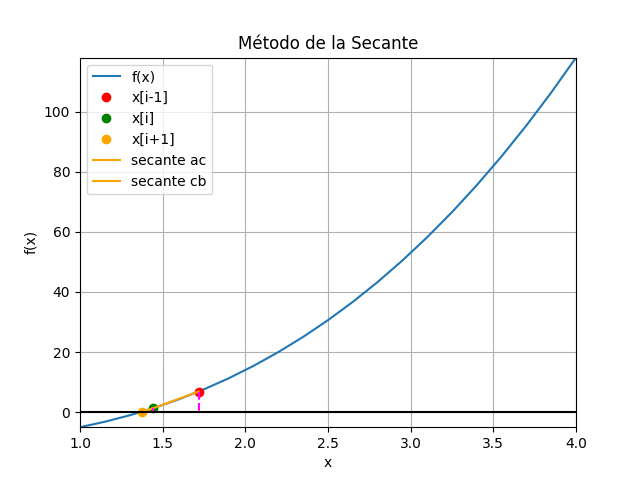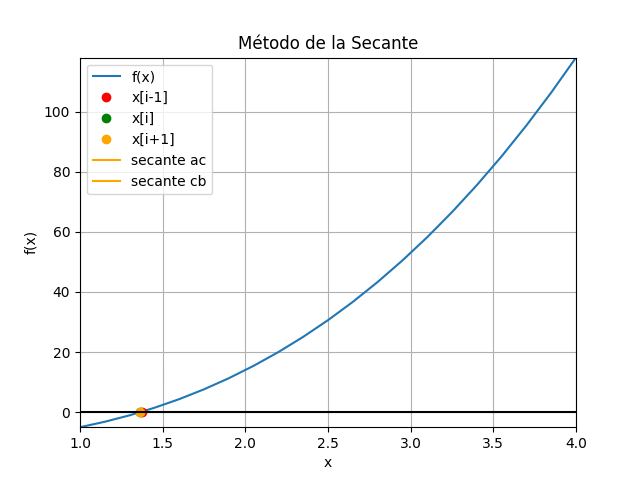
Método de la Secante con gráfico animado en Python
Instrucciones en Python
# Método de la secante # Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61) import numpy as np def secante_raiz_tabla(fx,a,b,tolera, iteramax=20, vertabla=True, precision=6): '''fx en forma numérica lambda Los valores de [a,b] son seleccionados desde la gráfica de la función ''' xi_1 = a xi = b itera = 0 tramo = np.abs(xi-xi_1) tabla = [] if vertabla==True: print('método de la Secante') print('i','[ x[i-1], xi, x[i+1], f[i-1], fi ]','tramo') np.set_printoptions(precision) while not(tramo<tolera or itera>iteramax): fi_1 = fx(xi_1) fi = fx(xi) xi1 = xi-fi*(xi_1 - xi)/(fi_1-fi) tramo = np.abs(xi1-xi) if vertabla==True: print(itera,np.array([xi_1,xi,xi1,fi_1,fi]),tramo) tabla.append([xi_1,xi,xi1,fi_1,fi]) xi_1 = xi xi = xi1 itera = itera + 1 if itera>=iteramax: xi = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') respuesta = xi tabla = np.array(tabla,dtype=float) return(respuesta,tabla) # PROGRAMA ---------------------- # INGRESO fx = lambda x: x**3 + 4*x**2 - 10 a = 1 b = 4 c = (a+b)/2 tolera = 0.001 tramos = 100 # PROCEDIMIENTO [raiz,tabla] = secante_raiz_tabla(fx,c,b,tolera, vertabla=True) # SALIDA print('raiz en :', raiz) # GRAFICA import matplotlib.pyplot as plt muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) xc = tabla[:,2] yc = fx(xc) plt.plot(xi,fi, label='f(x)') plt.plot([a,b],[fx(a),fx(b)],'o', color='red',label='[x0,f(x0)]') plt.scatter(xc,yc,color='orange', label='[c,f(c)]') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.grid() plt.legend() #plt.show() # GRÁFICO CON ANIMACION ###### import matplotlib.animation as animation xa = tabla[:,0] ya = tabla[:,3] xb = tabla[:,1] yb = tabla[:,4] xc = tabla[:,2] # Inicializa parametros de trama/foto narchivo = 'SecanteMetodo' # nombre archivo retardo = 700 # milisegundos entre tramas tramas = len(xa) # GRAFICA animada en fig_ani fig_ani, graf_ani = plt.subplots() graf_ani.set_xlim([a,b]) graf_ani.set_ylim([np.min(fi),np.max(fi)]) # Lineas y puntos base lineafx, = graf_ani.plot(xi,fi,label ='f(x)') puntoa, = graf_ani.plot(xa[0], ya[0],'o', color='red', label='x[i-1]') puntob, = graf_ani.plot(xb[0], yb[0],'o', color='green', label='x[i]') puntoc, = graf_ani.plot(xc[0], yc[0],'o', color='orange', label='x[i+1]') lineatan1, = graf_ani.plot([xa[0],xb[0]], [ya[0],yb[0]], color='orange',label='secante ac') lineatan2, = graf_ani.plot([xc[0],xb[0]], [0,yb[0]], color='orange',label='secante cb') linea_a, = graf_ani.plot([xa[0],xa[0]], [ya[0],0], color='magenta', linestyle='dashed') linea_b, = graf_ani.plot([xb[0],xb[0]], [0,yb[0]], color='magenta', linestyle='dashed') # Configura gráfica linea0 = graf_ani.axhline(0, color='k') graf_ani.set_title('Método de la Secante') graf_ani.set_xlabel('x') graf_ani.set_ylabel('f(x)') graf_ani.legend() graf_ani.grid() # Cada nueva trama def unatrama(i,xa,ya,xb,yb,xc): # actualiza cada punto, [] porque es solo un valor puntoa.set_xdata([xa[i]]) puntoa.set_ydata([ya[i]]) puntob.set_xdata([xb[i]]) puntob.set_ydata([yb[i]]) puntoc.set_xdata([xc[i]]) puntoc.set_ydata([0]) # actualiza cada linea linea_a.set_ydata([ya[i], 0]) linea_a.set_xdata([xa[i], xa[i]]) linea_b.set_ydata([0, yb[i]]) linea_b.set_xdata([xb[i], xb[i]]) lineatan1.set_ydata([ya[i], 0]) lineatan1.set_xdata([xa[i], xc[i]]) lineatan2.set_ydata([0, yb[i]]) lineatan2.set_xdata([xc[i], xb[i]]) return (puntoa, puntob, puntoc, linea_a, linea_b, lineatan1, lineatan2,) # Limpia trama anterior def limpiatrama(): puntoa.set_ydata(np.ma.array(xa, mask=True)) puntob.set_ydata(np.ma.array(xb, mask=True)) puntoc.set_ydata(np.ma.array(xc, mask=True)) linea_a.set_ydata(np.ma.array([0,0], mask=True)) linea_b.set_ydata(np.ma.array([0,0], mask=True)) lineatan1.set_ydata(np.ma.array([0,0], mask=True)) lineatan2.set_ydata(np.ma.array([0,0], mask=True)) return (puntoa, puntob, puntoc, linea_a, linea_b, lineatan1, lineatan2,) # contador de tramas i = np.arange(0,tramas,1) ani = animation.FuncAnimation(fig_ani,unatrama, i , fargs=(xa, ya, xb, yb, xc), init_func=limpiatrama, interval=retardo, blit=True) # Graba Archivo GIFAnimado y video ani.save(narchivo+'_animado.gif', writer='pillow') #ani.save(narchivo+'.mp4') plt.show()
GIF animado: [ Bisección ] [ Posicion Falsa ] [ Newton-Raphson ] [ Punto Fijo ] [ Secante ]