[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

---

1. Método del Punto fijo

Referencia: Burden 2.2 p41, Chapra 6.1 p143, Rodríguez 3.2 p44

El método del punto fijo es un método abierto, también llamado de iteración de un punto o sustitución sucesiva, que reordena la ecuación planteada para raíces de ecuaciones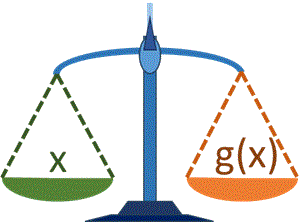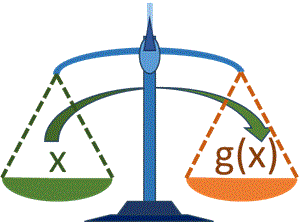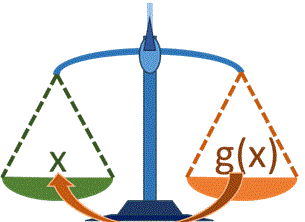

 f(x)= 0

separando una x al lado izquierdo de la igualdad.

x = g(x)

Esto permite buscar la intersección entre la recta Identidad y=x y la curva g(x), que es lo que quedó del lado derecho de la igualdad.
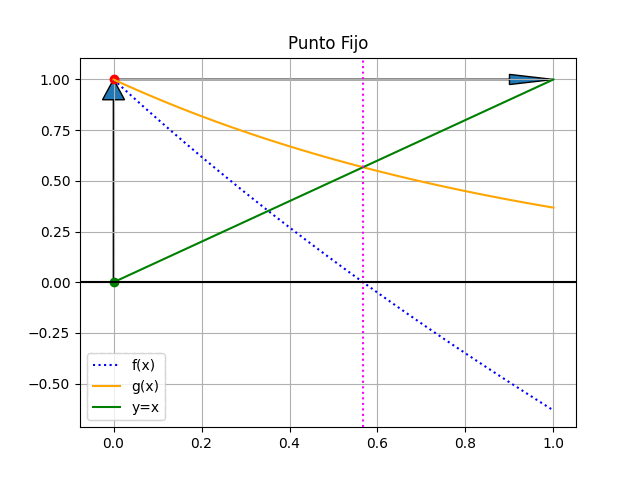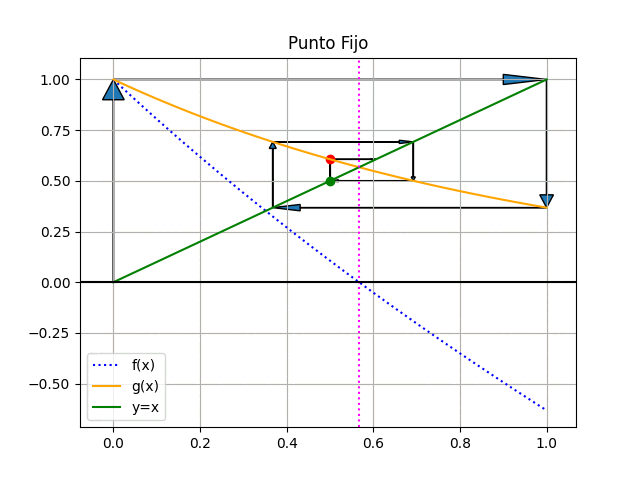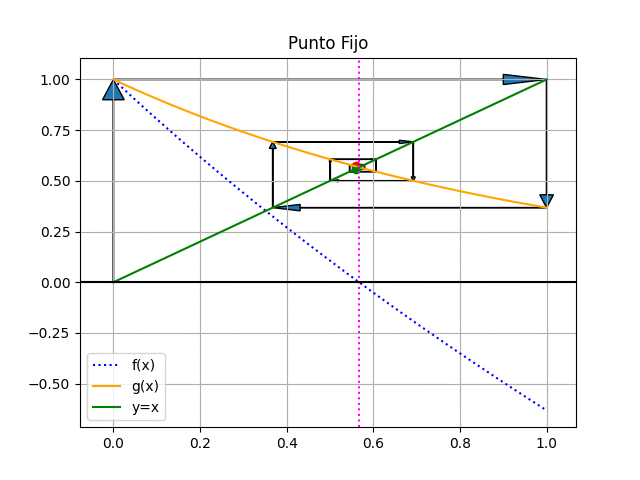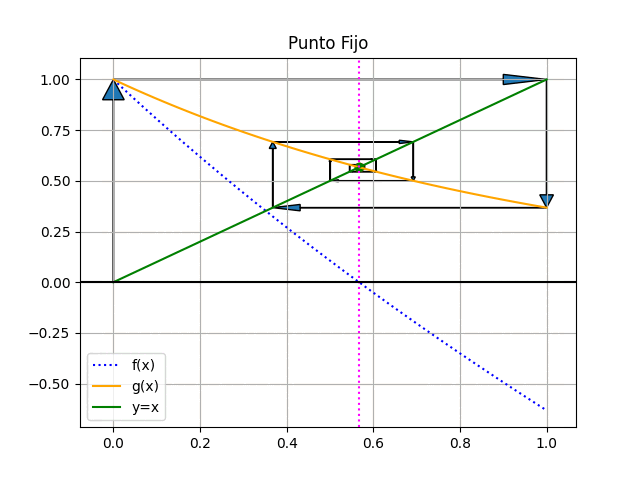
Una representación gráfica del proceso de muestra en la gráfica.

Observe que la raíz de f(x) se encuentra en el mismo valor de x donde ocurre la intersección entre la recta identidad y=x , en color verde, y la función g(x), en color naranja. Como referencia, se usa la linea vertical en x=raíz en color morado.

El método consiste en establecer un punto inicial x₀ para la búsqueda, a partir del cual se calcula el valor g(x₀). En la siguiente iteración el nuevo valor para x es g(x₀), que se refleja en la recta identidad y nuevamente se usa para calcular g(x).

El resultado iterativo se muestra en la figura animada, donde se observa que el resultado es convergente.

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

---

2. Ejemplos

Se muestran algunos ejemplos para destacar lo indicado de forma gráfica.

Ejemplo 1

f(x):e^{-x} - x = 0

se reordena para tener:

x = e^{-x} g(x) = e^{-x}

---

Ejemplo 2

f(x): x^2 - 2x -3 = 0

se reordena para tener:

x = \frac {x^2 - 3}{2} g(x) = \frac {x^2 - 3}{2}

---

Ejemplo 3

f(x): \sin (x) = 0

puede ser complicado despejar x, por lo que se simplifica el proceso sumando x en ambos lados.

x = \sin (x) + x g(x) = \sin (x) + x

El método proporciona una fórmula para predecir un valor nuevo de x en función del valor anterior:

x_{i+1} = g(x_i)

con error aproximado calculado como:

\epsilon_a = \left| \frac{x_{i+1} - x_i}{x_{i+1}} \right| 100\%

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]

---

4. Tarea

Plantee como usar los siguientes conceptos:

• ¿cuál sería el valor de tolerancia?
• ¿parámetros de inicio?
• compare con con otro método conocido
• Revisar el resultado cuando no se cumple que |g'(x)|<1

[ Punto fijo ][ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]