Referencia: Chapra 17.2 p482, Burden 8.1 p501
Una alternativa a usar transformaciones ente los ejes para ajustar las curvas es usar regresión polinomial extendiendo el procedimiento de los mínimos cuadrados.
Suponga que la curva se ajusta a un polinomio de segundo grado o cuadrático
y = a_0 + a_1 x + a_2 x^2 +eusando nuevamente la suma de los cuadrados de los residuos, se tiene,
S_r = \sum_{i=1}^n (y_i- (a_0 + a_1 x_i + a_2 x_i^2))^2para minimizar los errores se deriva respecto a cada coeficiente: a0, a1, a2
\frac{\partial S_r}{\partial a_0} = -2\sum (y_i- a_0 - a_1 x_i - a_2 x_i^2) \frac{\partial S_r}{\partial a_1} = -2\sum x_i (y_i- a_0 - a_1 x_i - a_2 x_i^2) \frac{\partial S_r}{\partial a_2} = -2\sum x_i^2 (y_i- a_0 - a_1 x_i - a_2 x_i^2)Se busca el mínimo de cada sumatoria, igualando a cero la derivada y reordenando, se tiene el conjunto de ecuaciones:
a_0 (n) + a_1 \sum x_i + a_2 \sum x_i^2 = \sum y_i a_0 \sum x_i + a_1 \sum x_i^2 + a_2 \sum x_i^3 =\sum x_i y_i a_0 \sum x_i^2 + a_1 \sum x_i^3 + a_2 \sum x_i^4 =\sum x_i^2 y_icon incógnitas a0, a1 y a2, cuyos coeficientes se pueden evaluar con los puntos observados. Se puede usar un médoto directo de la unidad 3 para resolver el sistema de ecuaciones Ax=B.
\begin{bmatrix} n & \sum x_i & \sum x_i^2 \\ \sum x_i & \sum x_i^2 & \sum x_i^3 \\ \sum x_i^2 & \sum x_i^3 & \sum x_i^4 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \\ \sum x_i^2 y_i \end{bmatrix}C = np.linalg.solve(A,B)y = C_0 + C_1 x + C_2 x^2
El error estándar se obtiene como:
S_{y/x} = \sqrt{\frac{S_r}{n-(m+1)}}siendo m el grado del polinomio usado, para el caso presentado m = 2
S_r = \sum{(yi-fi)^2}Sr es la suma de los cuadrados de los residuos alrededor de la línea de regresión.
| xi | yi | (yi-ymedia)2 | (yi-fi)2 |
|---|---|---|---|
| ... | ... | ||
| ... | ... | ||
| ∑yi | St | Sr |
siendo St la suma total de los cuadrados alrededor de la media para la variable dependiente y. Este valor es la magnitud del error residual asociado con la variable dependiente antes de la regresión.
El algoritmo se puede desarrollar de forma semejante a la presentada en la sección anterior,
Ejercicio Chapra 17.5 p484
Los datos de ejemplo para la referencia son:
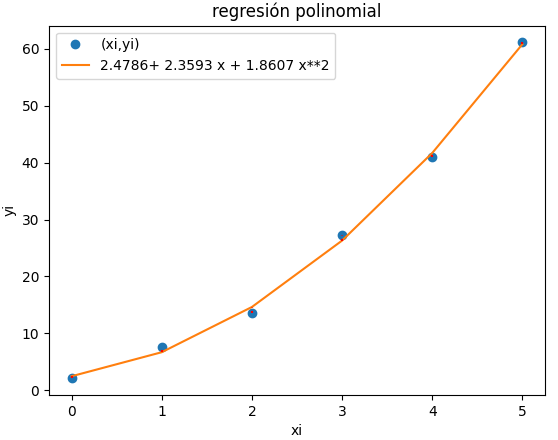
xi = [0, 1, 2, 3, 4, 5] yi = [2.1, 7.7, 13.6, 27.2, 40.9, 61.1]
resultado de algoritmo:
fx = 1.86071428571429*x**2 + 2.35928571428571*x + 2.47857142857143 Syx = 1.117522770621316 coef_determinacion r2 = 0.9985093572984048 99.85% de los datos se describe con el modelo >>>
Instrucciones en Python
# regresion con polinomio grado m=2 import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO xi = [0, 1, 2, 3, 4, 5] yi = [2.1, 7.7, 13.6, 27.2, 40.9, 61.1] m = 2 # PROCEDIMIENTO xi = np.array(xi) yi = np.array(yi) n = len(xi) # llenar matriz a y vector B k = m + 1 A = np.zeros(shape=(k,k),dtype=float) B = np.zeros(k,dtype=float) for i in range(0,k,1): for j in range(0,i+1,1): coeficiente = np.sum(xi**(i+j)) A[i,j] = coeficiente A[j,i] = coeficiente B[i] = np.sum(yi*(xi**i)) # coeficientes, resuelve sistema de ecuaciones C = np.linalg.solve(A,B) # polinomio x = sym.Symbol('x') f = 0 fetiq = 0 for i in range(0,k,1): f = f + C[i]*(x**i) fetiq = fetiq + np.around(C[i],4)*(x**i) fx = sym.lambdify(x,f) fi = fx(xi) # errores ym = np.mean(yi) xm = np.mean(xi) errado = fi - yi sr = np.sum((yi-fi)**2) syx = np.sqrt(sr/(n-(m+1))) st = np.sum((yi-ym)**2) # coeficiente de determinacion r2 = (st-sr)/st r2_porcentaje = np.around(r2*100,2) # SALIDA print('ymedia = ',ym) print(' f =',f) print('coef_determinacion r2 = ',r2) print(str(r2_porcentaje)+'% de los datos') print(' se describe con el modelo') # grafica plt.plot(xi,yi,'o',label='(xi,yi)') # plt.stem(xi,yi, bottom=ym) plt.plot(xi,fi, color='orange', label=fetiq) # lineas de error for i in range(0,n,1): y0 = np.min([yi[i],fi[i]]) y1 = np.max([yi[i],fi[i]]) plt.vlines(xi[i],y0,y1, color='red', linestyle = 'dotted') plt.xlabel('xi') plt.ylabel('yi') plt.legend() plt.title('Regresion polinomial grado '+str(m)) plt.show()